Embed presentation
Downloaded 30 times


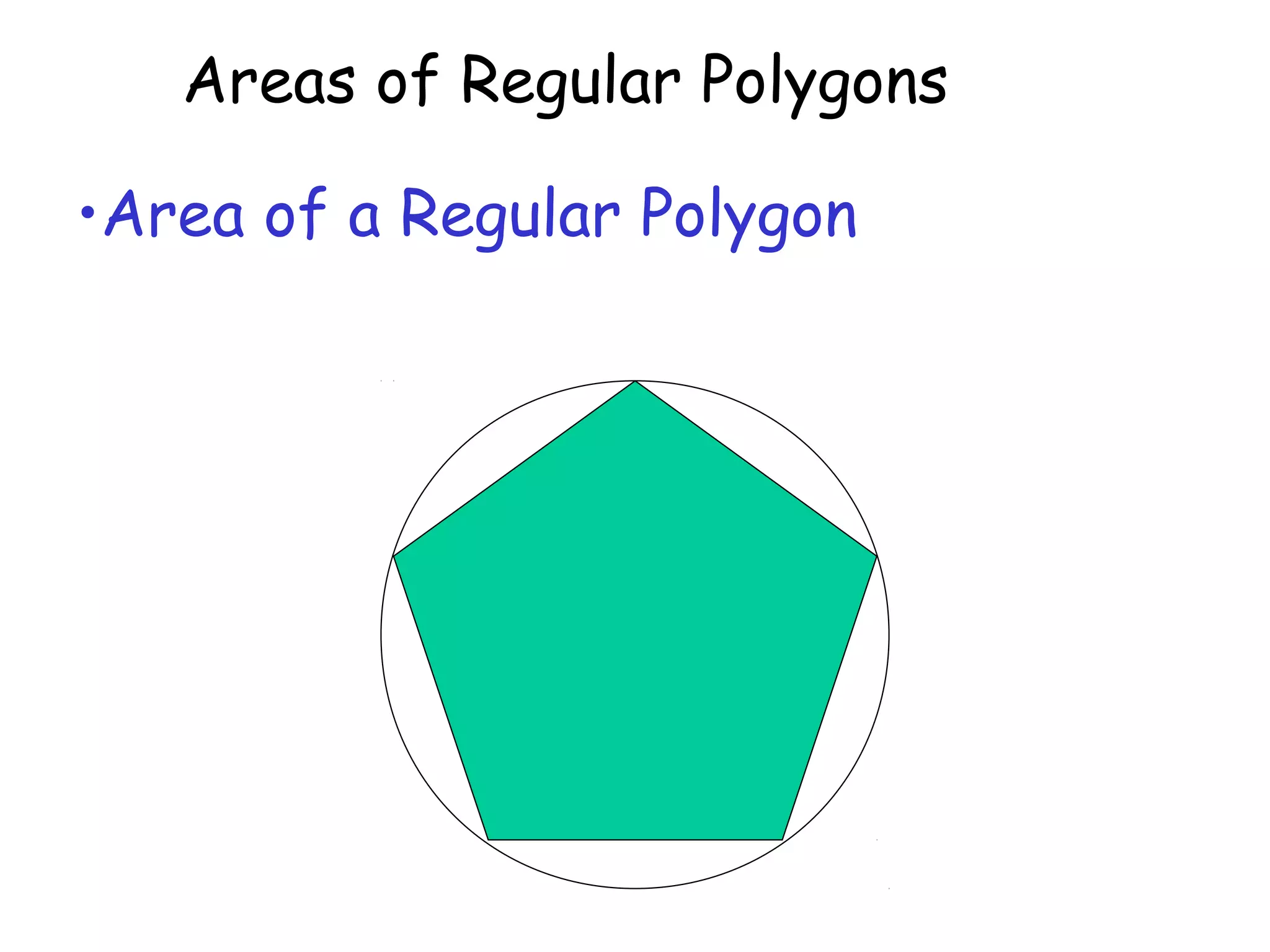
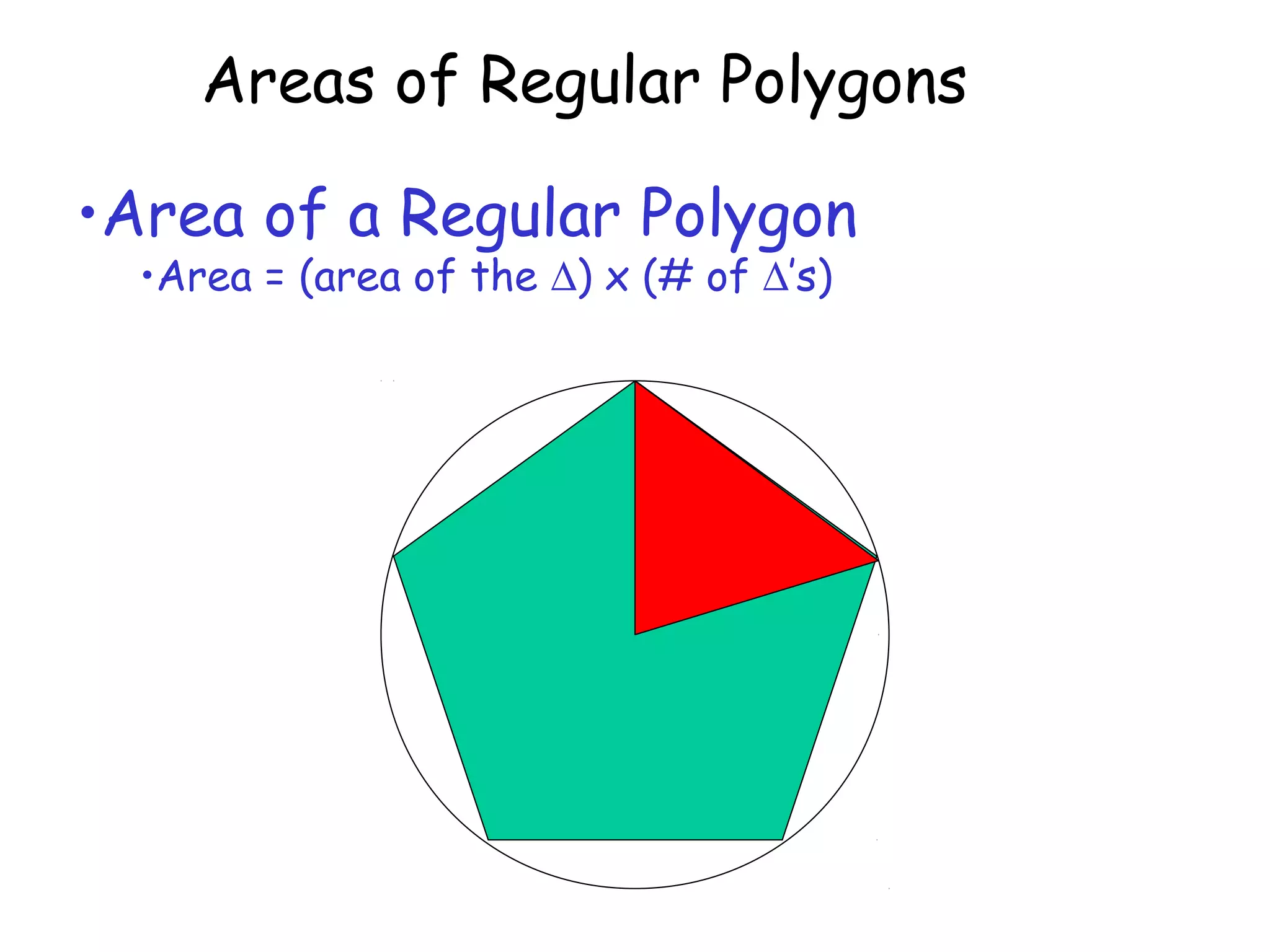
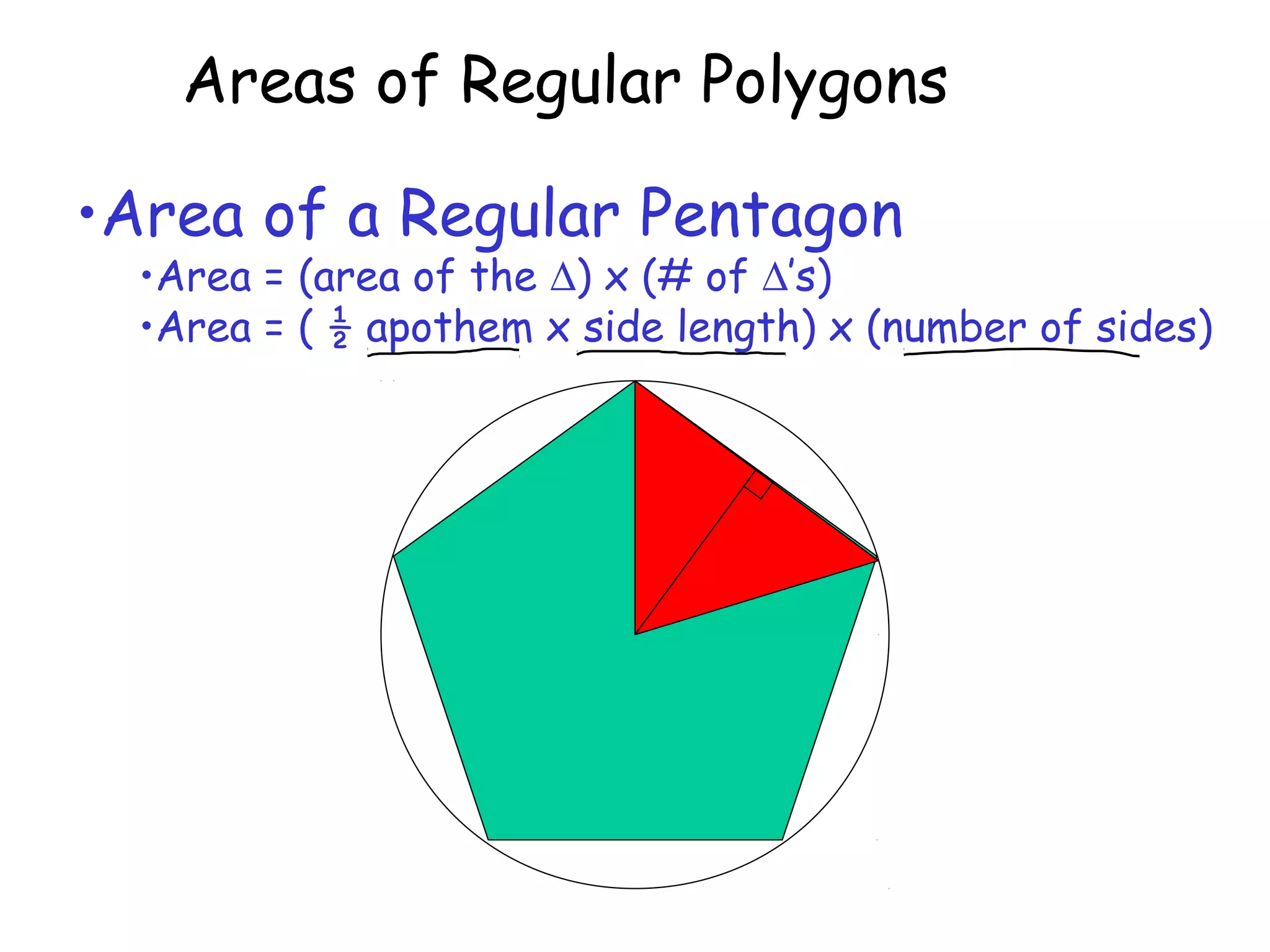
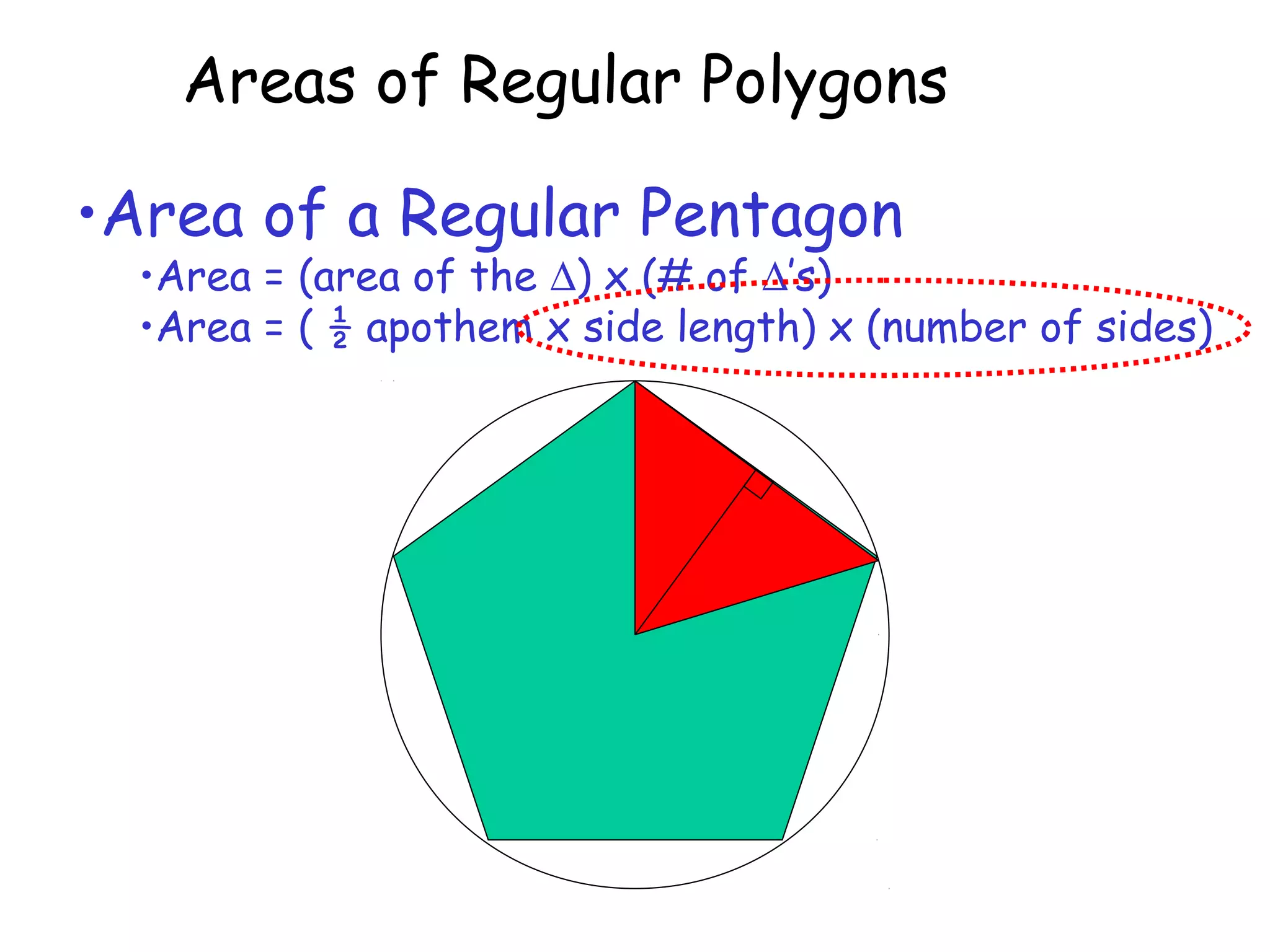
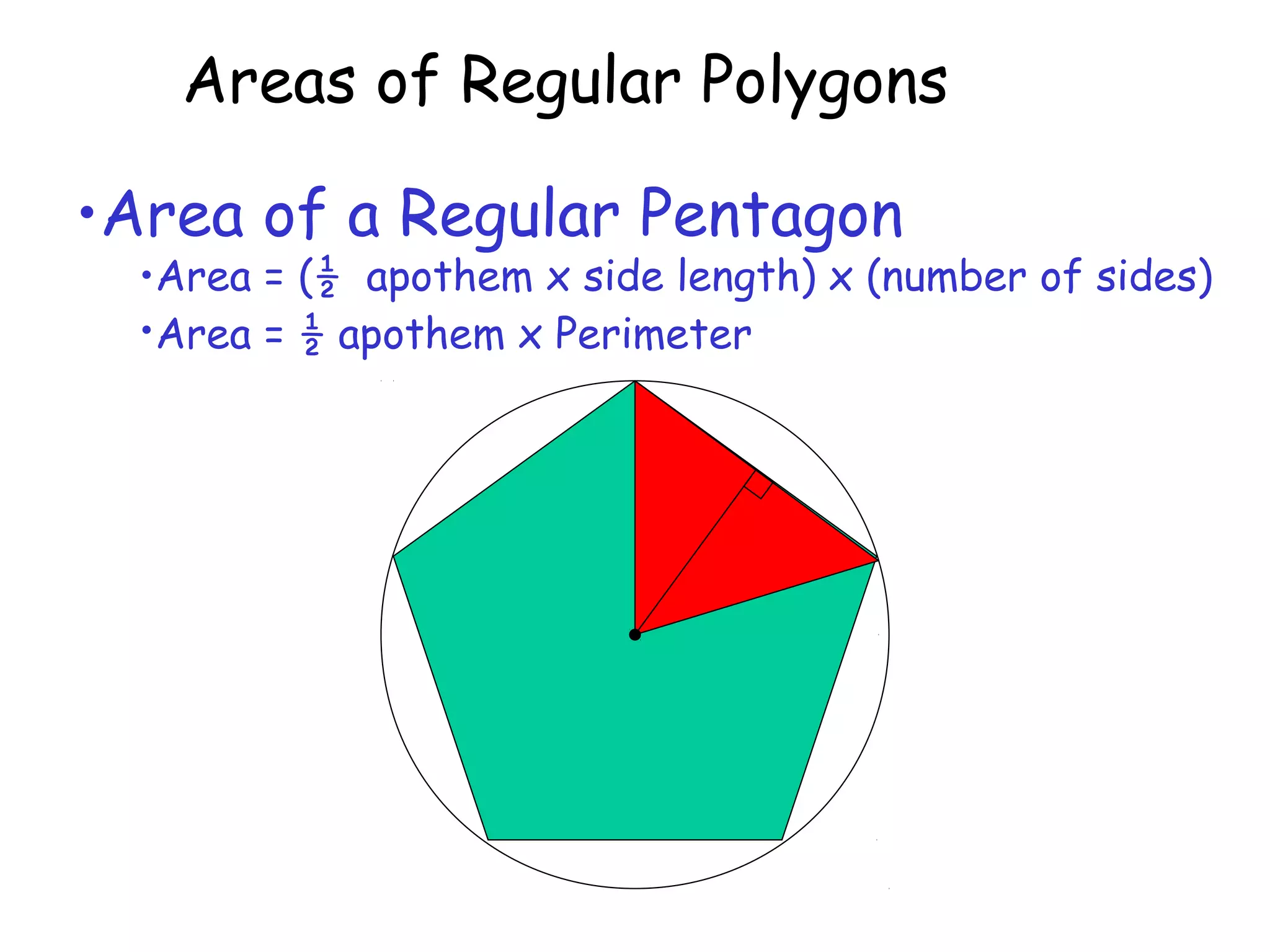

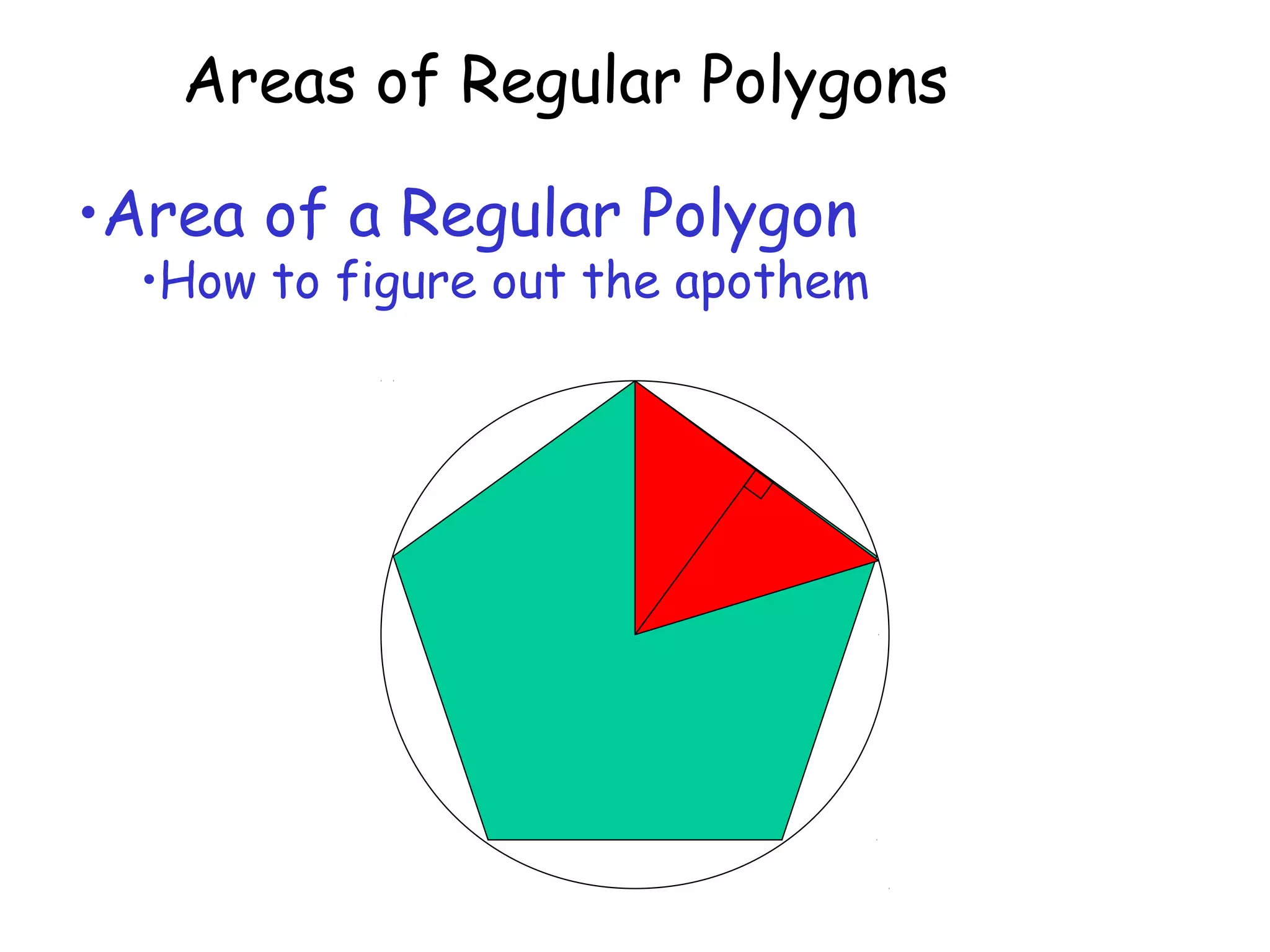

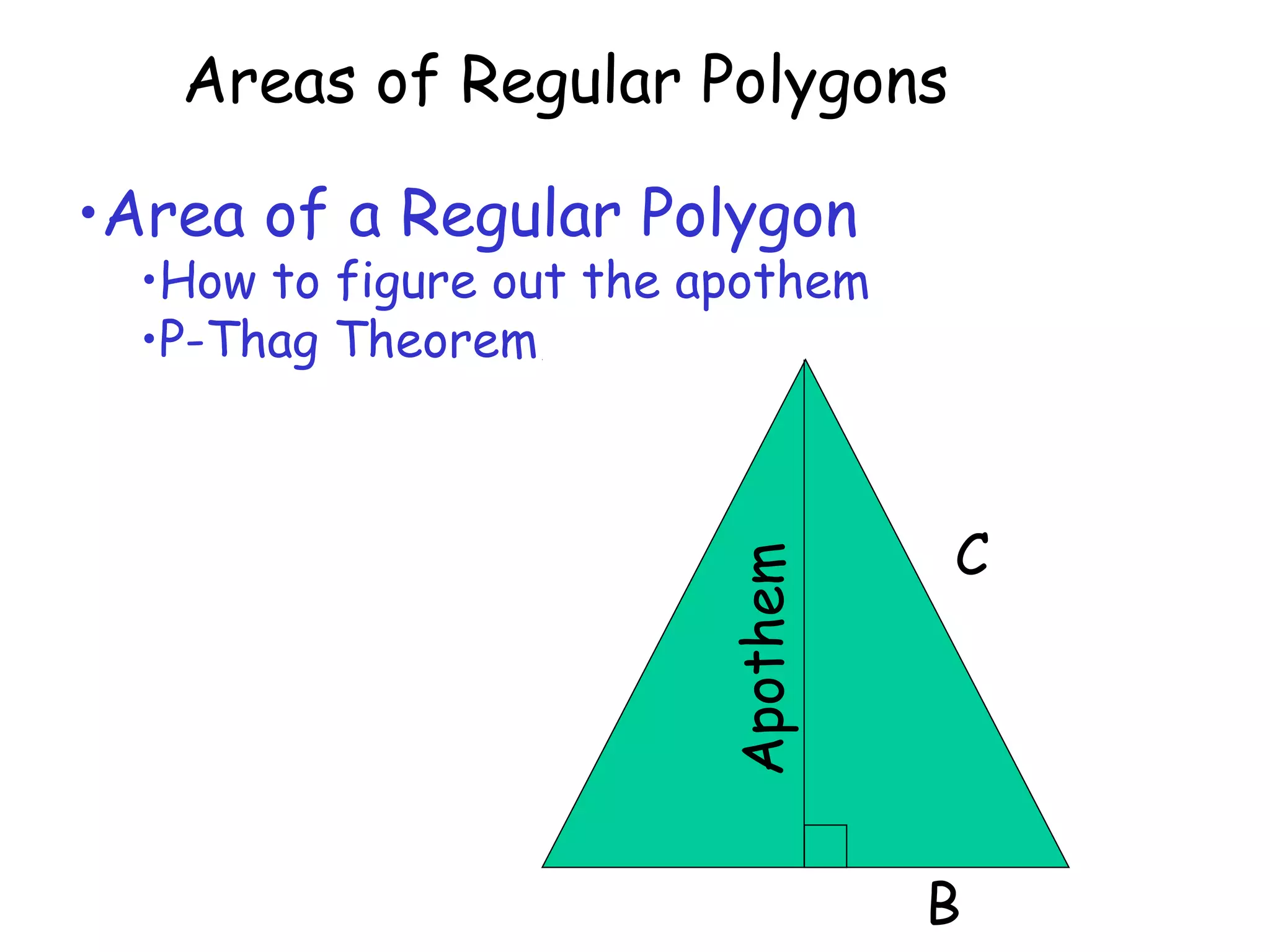




This document discusses calculating the areas of regular polygons. It states that the area of any regular polygon can be calculated as one half of the apothem multiplied by the perimeter. The apothem is the distance from the center of the polygon to the midpoint of any side. It can be calculated using trigonometry by relating it to the central angle of the polygon using tangent or cosine.














