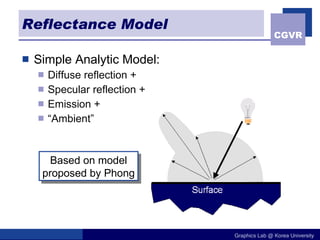
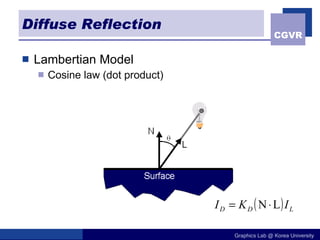
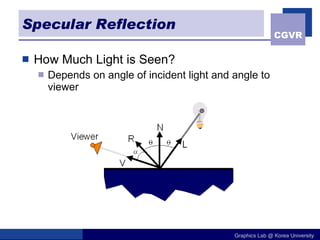
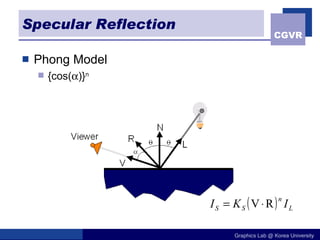
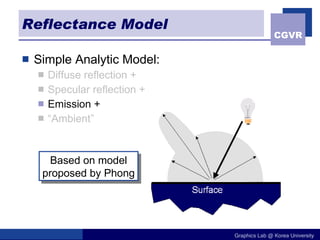
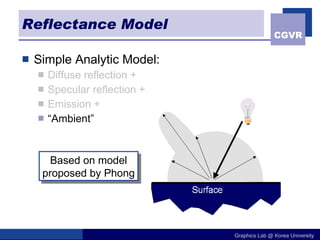
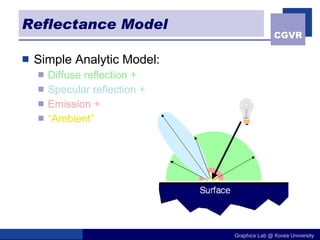
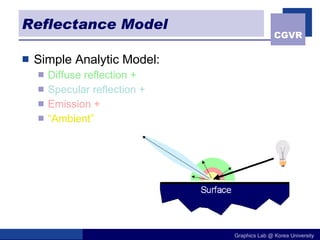
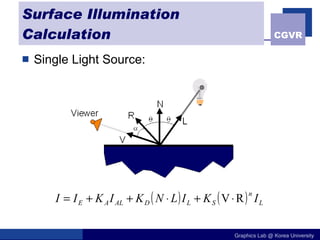
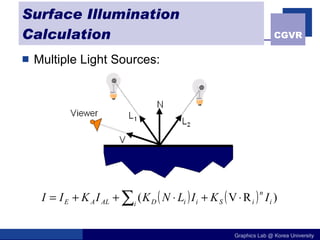
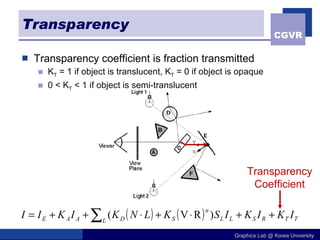
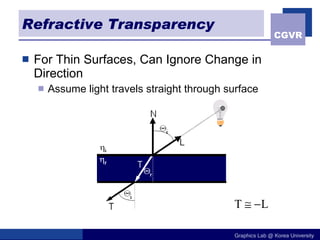
The document discusses illumination models in computer graphics. It covers direct illumination from light sources and scattering at surfaces. It also discusses global illumination techniques like shadows, reflections and refractions using ray tracing. Common lighting models include point lights, directional lights and spot lights for light sources, and Lambertian and Phong reflection models for surfaces. Global illumination methods recursively trace rays to account for effects of indirect lighting. Key terms discussed include radiant power, radiant intensity, radiance, irradiance and radiosity.

1. Illumination Model 고려대학교 컴퓨터 그래픽스 연구실

2. Illumination How do We Compute Radiance for a Sample Ray? Must derive computer models for ... Emission at light sources Scattering at surfaces Reception at the camera Wireframe Without Illumination Direct Illumination

3. Overview Direct Illumination Emission at light sources Scattering at surfaces Global Illumination Shadows Refractions Inter-object reflections Direct Illumination

4. Overview Direct Illumination Emission at light sources Scattering at surfaces Global Illumination Shadows Refractions Inter-object reflections Direct Illumination

5. Modeling Light Source I L ( x,y,z,  ) Describes the intensity of energy, Leaving a light source Arriving at location(x,y,z) From direction (  ) With wavelength 

6. Empirical Model Ideally Measure Irradiant Energy for “All” Situations Too much storage Difficult in practice

7. Light Source Model Simple Mathematical Models: Point light Directional light Spot light

8. Point Light Source Models Omni-Directional Point Source (E.g., Bulb) Intensity (I 0 ) Position (px, py, pz) Factors (k c , k l , k q ) for attenuation with distance (d)

9. Directional Light Source Models Point Light Source at Infinity (E.g., Sun) Intensity (I 0 ) Direction (dx,dy,dz) No attenuation with distance

10. Spot Light Source Models Point Light Source with Direction (E.g., Luxo) Intensity (I 0 ), Position (px, py, pz) Direction (dx, dy, dz) Attenuation

11. Overview Direct Illumination Emission at light sources Scattering at surfaces Global Illumination Shadows Refractions Inter-object reflections Direct Illumination

12. Modeling Surface Reflection R s (  ,  ) Describes the amount of incident energy Arriving from direction (  ) Leaving in direction (  ,  ) With wavelength 

13. Empirical Model Ideally Measure Radiant Energy for “All” Combinations of Incident Angles Too much storage Difficult in practice

14. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient” Based on model proposed by Phong

15. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient” Based on model proposed by Phong

16. Diffuse Reflection Assume Surface Reflects Equally in All Directions Examples: chalk, clay

17. Diffuse Reflection How Much Light is Reflected? Depends on angle of incident light dL  dA  cos 

18. Diffuse Reflection Lambertian Model Cosine law (dot product)

19. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient” Based on model proposed by Phong

20. Specular Reflection Reflection is Strongest Near Mirror Angle Examples: mirrors, metals

21. Specular Reflection How Much Light is Seen? Depends on angle of incident light and angle to viewer

22. Specular Reflection Phong Model {cos(  )} n

23. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient” Based on model proposed by Phong

24. Emission Represents Light Emitting Directly From Polygon Emission ≠ 0

25. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient” Based on model proposed by Phong

26. Ambient Term Represents Reflection of All Indirect Illumination This is a total hack (avoids complexity of global illumination)!

27. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient”

28. Reflectance Model Simple Analytic Model: Diffuse reflection + Specular reflection + Emission + “ Ambient”

29. Reflectance Model Sum Diffuse, Specular, Emission, and Ambient

30. Surface Illumination Calculation Single Light Source:

31. Surface Illumination Calculation Multiple Light Sources:

32. Overview Direct Illumination Emission at light sources Scattering at surfaces Global Illumination Shadows Refractions Inter-object reflections Global Illumination

33. Global Illumination

34. Shadows Shadow Terms Tell Which Light Sources are Blocked Cast ray towards each light source L i S i = 0 if ray is blocked, S i = 1 otherwise Shadow Term

35. Ray Casting Trace Primary Rays from Camera Direct illumination from unblocked lights only

36. Recursive Ray Tracing Also Trace Secondary Rays from Hit Surfaces Global illumination from mirror reflection and transparency

37. Mirror Reflection Trace Secondary Ray in Direction of Mirror Reflection Evaluate radiance along secondary ray and include it into illumination model Radiance for mirror reflection ray

38. Transparency Trace Secondary Ray in Direction of Refraction Evaluate radiance along secondary ray and include it into illumination model Radiance for refraction ray

39. Transparency Transparency coefficient is fraction transmitted K T = 1 if object is translucent, K T = 0 if object is opaque 0 < K T < 1 if object is semi-translucent Transparency Coefficient

40. Refractive Transparency For Thin Surfaces, Can Ignore Change in Direction Assume light travels straight through surface

41. Refractive Transparency For Solid Objects, Apply Snell’s Law:  r sin  r  i  sin  i 

42. Summary Direct Illumination Ray casting Usually use simple analytic approximations for light source emission and surface reflectance Global illumination Recursive ray tracing Incorporate shadows, mirror reflections, and pure refractions

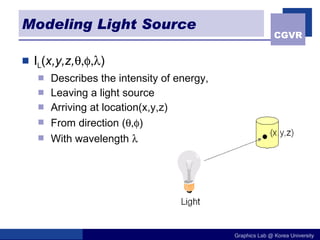
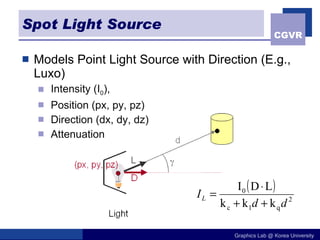
43. Illumination Terminology Radiant power [flux] ( Φ ) Rate at which light energy is transmitted (in Watts). Radiant Intensity (I) Power radiated onto a unit solid angle in direction( in Watt/sr) e.g.: energy distribution of a light source (inverse square law) Radiance (L) Radiant intensity per unit projected surface area( in Watts/m 2 sr) e.g.: light carried by a single ray (no inverse square law) Irradianc (E) Incident flux density on a locally planar area (in Watts/m 2 ) Radiosity (B) Exitant flux density from a locally planar area ( in Watts/m 2 )