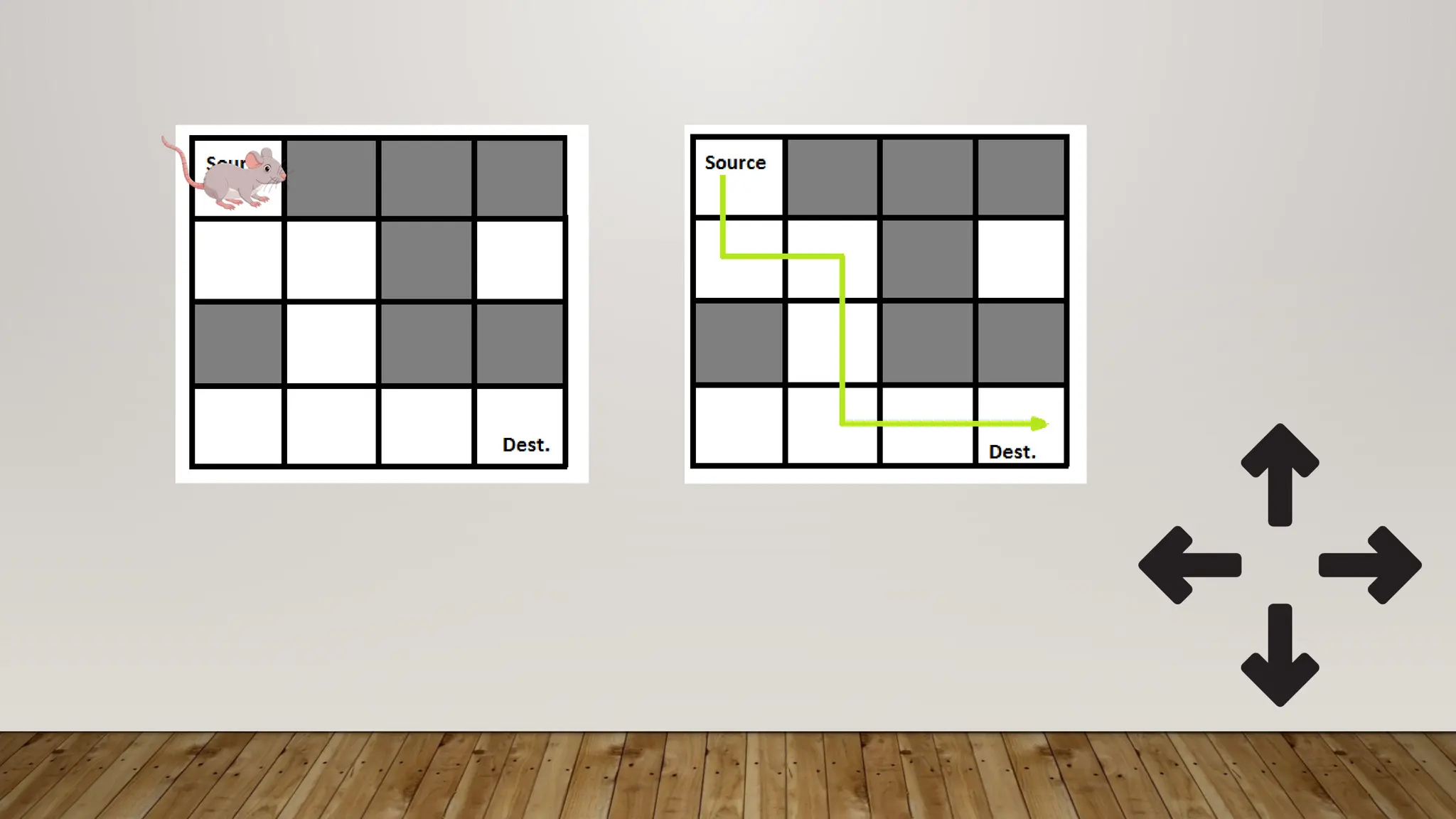
The document describes methods for solving maze problems using algorithms like backtracking and dynamic programming, including memoization and tabulation approaches. It outlines the processes for each method, detailing their recursive nature, solution construction, and time/space complexities. The examples provided illustrate how to implement these techniques in code to count paths through a maze.

1. RAT IN A MAZE

3. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1

4. BACKTRACKING APPROACH
• How BacktrackingWorks:
1.Start with an empty solution and build it step by step.
2.Choose an option and add it to the solution.
3.Check if the current solution is valid:
1. If valid, continue to build the solution.
2. If not valid, remove the last choice (backtrack) and try a different option.
4.Repeat the process until a solution is found or all possibilities are exhausted.

5. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1

6. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1

7. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1

8. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1

9. function solveMaze(maze):
N = size of maze # Assume square matrix
# Create solution matrix to store the path
solution = matrix of size N x N initialized to 0
if solveMazeUtil(maze, 0, 0, solution) == False:
print("No solution exists")
return False
printSolution(solution)
returnTrue
# Recursive utility function to solve the maze problem
function solveMazeUtil(maze, x, y, solution):
# Base case: If x, y is the destination (N-1, N-1), return True
if x == N-1 and y == N-1:
solution[x][y] = 1 # Mark this cell in the solution path
return True

10. # Check if maze[x][y] is a valid cell to move into
if isSafe(maze, x, y):
solution[x][y] = 1 # Mark this cell as part of the solution path
# Move Up (x, y - 1)
if solveMazeUtil(maze, x, y - 1, solution):
return True
# Move Left (x - 1, y)
if solveMazeUtil(maze, x - 1, y, solution):
return True
# If moving in x direction doesn't work, move down in the y direction
if solveMazeUtil(maze, x, y + 1, solution):
return True
# Move forward in the x (right) direction
if solveMazeUtil(maze, x + 1, y, solution):
return True
# If neither direction works, backtrack: unmark this cell
solution[x][y] = 0
return False
return False

11. # Check if x, y is a valid move (i.e., within maze boundaries and
not blocked)
function isSafe(maze, x, y):
return (x >= 0 and x < N and y >= 0 and y < N and maze[x]
[y] == 1)
# Utility function to print the solution path
function printSolution(solution):
for i from 0 to N-1:
for j from 0 to N-1:
print(solution[i][j], end = " ")
print("")

12. TIME COMPLEXITY AND SPACE COMPLEXITY
• Time Complexity: O(4^(N^2))
• Space complexity: O(N^2)

13. DYNAMIC PROGRAMMING APPROACH
• Dynamic Programming (DP) is a method used to solve complex problems by
breaking them down into simpler subproblems.
• It is particularly useful for optimization problems where the solution can be built from
solutions to smaller instances of the same problem.The key idea is to store the results of
subproblems so they do not need to be recalculated, which saves computation time.
• Types of Dynamic Programming:
1. Memoization (Top-Down Approach)
2. Tabulation (Bottom-Up Approach)

14. TABULATION APPROACH
• HowTabulation Works (Bottom-Up Approach):
1.Identify the problem and determine the smallest subproblems.
2.Solve each subproblem iteratively and store the results in a table
(tablution).
3.Use the stored results to build the solution to larger subproblems.
4.Continue the process until the solution to the original problem is found.

15. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
MAZE: DPTable:

16. 0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 1 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 1 0 0
1 0 0 0
0 0 0 0
0 0 0 0
1 1 0 0
1 2 2 2
0 0 0 0
0 0 0 0
1 1 0 0
1 2 2 2
0 2 0 2
0 0 0 0
1 1 0 0
1 2 2 2
0 2 0 2
0 2 2 4
ANS:
DP[3][3] = 4

17. int countPaths(int maze[][4], int n, int m) {
int dp[n][m];
// Initialize the starting point
dp[0][0] = maze[0][0] == 1 ? 1 : 0;
// Fill the first row
for (int j = 1; j < m; j++) {
if (maze[0][j] == 1) {
dp[0][j] = dp[0][j - 1];
} else {
dp[0][j] = 0;
}
}
// Fill the first column
for (int i = 1; i < n; i++) {
if (maze[i][0] == 1) {
dp[i][0] = dp[i - 1][0];
} else {
dp[i][0] = 0;
}
}

18. // Fill the rest of the dp table
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
if (maze[i][j] == 1) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
} else {
dp[i][j] = 0;
}
}
}
return dp[n - 1][m - 1]; // Return the number of ways to reach the bottom-right corner
}
int main() {
int maze[4][4] = {
{1, 1, 0, 1},
{1, 1, 1, 1},
{0, 1, 0, 1},
{1, 1, 1, 1}
};
int n = 4, m = 4;
printf("Number of paths: %dn", countPaths(maze, n, m));
return 0;
}

19. TIME COMPLEXITY AND SPACE COMPLEXITY
• Time Complexity: O(N x M)
• Space complexity: O(N x M)

20. MEMOIZATION APPROACH
• How Memoization Works (Top-Down Approach):
1.Start with a problem and break it down into smaller subproblems.
2.Solve each subproblem recursively, storing the result (memoization).
3.If a subproblem is already solved, use the stored result instead of
recalculating it.
4.Continue this process until the final solution is built using the results of
subproblems.

21. 1 1 0 1
1 1 1 1
0 1 0 1
1 1 1 1
1 1 0 0
1 2 2 2
0 2 0 2
0 2 2 4
MAZE: DPTable:

22. int helper(int maze[][4], int i, int j) {
// If out of bounds or cell is blocked, return 0
If (i < 0 || j < 0 || maze[i][j] == 0) { return 0; }
// If at the starting cell, return 1
if (i == 0 && j == 0) { return 1; }
// If already computed, return the stored value
if (dp[i][j] != -1) { return dp[i][j]; }
// Compute the number of ways from the top and left cells
int up = helper(maze, i - 1, j);
// From above int left = helper(maze, i, j - 1);
// From the left // Store the result in dp table
dp[i][j] = up + left;
return dp[i][j]; }
int countPaths(int maze[][4], int n, int m) {
// Initialize the dp table with -1
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
dp[i][j] = -1; } } // Call the helper function for the bottom-right corner return
helper(maze, n - 1, m - 1); }

23. int countPaths(int maze[][4], int n, int m) {
// Initialize the dp table with -1
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
dp[i][j] = -1;
}
}
// Call the helper function for the bottom-right corner
return helper(maze, n - 1, m - 1);
}

24. TIME COMPLEXITY AND SPACE COMPLEXITY
• Time Complexity: O(N x M)
• Space complexity: O(N x M)