This document discusses monadic programming (MP) in Clojure. It begins with introductions to monads and monadic programming in Haskell. It then discusses reasons for using MP in Clojure despite it not having static typing or being purely functional. It explains two libraries for MP in Clojure - clojure.algo.monads and funcool/cats - and how they implement monads using macros and protocols. Examples are given of using monads for error handling in a reverse Polish notation calculator and for representing probability distributions.

1. MP in Clojure
~ herding cats with clj ~

2. Self-introduction
/laʒenɔʁɛ̃k/ カマイルカlagénorhynque
(defprofile lagénorhynque
:name "Kent OHASHI"
:languages [Clojure Haskell Python Scala
English français Deutsch русский]
:interests [programming language-learning mathematics]
:contributing [github.com/japan-clojurians/clojure-site-ja])

3. Clojure × MP

4. Contents
1. What is MP?
2. Why MP in Clojure?
3. How MP in Clojure?
4. Examples

5. What is MP?

6. programming with monads
cf. FP = functional programming
MP = monadic programming

7. de nition of Monad in Haskell
GHC.Base#Monad
class Applicative m => Monad m where
(>>=) :: forall a b. m a -> (a -> m b) -> m b
(>>) :: forall a b. m a -> m b -> m b
m >> k = m >>= _ -> k
{-# INLINE (>>) #-}
return :: a -> m a
return = pure
fail :: String -> m a
fail s = errorWithoutStackTrace s

8. monads in Haskell
型クラス Monad のインスタンス
>>= : m a -> (a -> m b) -> m b
return : a -> m a
モナド則( )を満たす
シンプルで合成可能な構造 → 様々な形で利⽤可能
do 記法というシンタックスシュガー
monad laws

9. e.g.
※ #渋⾕ java なので⼀応 Java の例から^_^;
java.util.Optional
jshell> Optional<Integer> a = Optional.of(2)
a ==> Optional[2]
jshell> Optional<Integer> b = Optional.of(3)
b ==> Optional[3]
jshell> a.flatMap( x -> // with `flatMap` & `map`
...> b.map( y ->
...> x * y
...> )
...> )
$3 ==> Optional[6]

10. e.g. scala.Option
scala> val a = Some(2)
a: Some[Int] = Some(2)
scala> val b = Some(3)
b: Some[Int] = Some(3)
scala> a.flatMap { x => // with `flatMap` & `map`
| b.map { y =>
| x * y
| }
| }
res0: Option[Int] = Some(6)
scala> for { // with `for` expression
| x <- a
| y <- b
| } yield x * y
res1: Option[Int] = Some(6)

11. e.g. Prelude.Maybe
> a = Just 2
> b = Just 3
> :{ -- with `>>=` & `return`
| a >>= x ->
| b >>= y ->
| return $ x * y
| :}
Just 6
> :{ -- with `do` notation
| do
| x <- a
| y <- b
| return $ x * y
| :}
Just 6

12. e.g. cats.monad.maybe
user=> (require '[cats.core :as m]
#_=> '[cats.monad.maybe :as maybe])
nil
user=> (def a (maybe/just 2))
#'user/a
user=> (def b (maybe/just 3))
#'user/b
user=> (m/>>= a (fn [x] ; with `>>=` & `return`
#_=> (m/>>= b (fn [y]
#_=> (m/return (* x y))))))
#<Just 6>
user=> (m/mlet [x a ; with `mlet` macro
#_=> y b]
#_=> (m/return (* x y)))
#<Just 6>

13. Why MP in Clojure?

14. MP in Clojure
Clojureでは
モナドは必須の機能ではないが……
静的型付け&純粋関数型の⾔語ではないが……
シンプルで汎⽤的なDSL構築フレームワーク
Haskellなどで有⽤なアイディアが活かせる
⇒ Clojureでも MP してみよう (*> ᴗ •*)ゞ

15. How MP in Clojure?

16. MP libraries in Clojure
clojure/algo.monads
Macros for defining monads, and
definition of the most common
monads
funcool/cats
Category Theory and Algebraic
abstractions for Clojure and
ClojureScript.

17. how to support MP in Clojure
feature algo.monads cats
Monad type class plain Map data protocol
do notation macro macro
context inference (n/a) protocol

18. anatomy of algo.monads
user=> (require '[clojure.algo.monads :as m])
nil
user=> (m/domonad m/maybe-m
#_=> [x 2
#_=> y 3]
#_=> (* x y))
6

19. macroexpand-1
clojure.algo.monads/with-monad ?
user=> (macroexpand-1
#_=> '(m/domonad m/maybe-m
#_=> [x 2
#_=> y 3]
#_=> (* x y)))
(clojure.algo.monads/with-monad m/maybe-m
(m-bind 2 (fn [x]
(m-bind 3 (fn [y]
(m-result (* x y)))))))

20. macroexpand-1 once more
clojure.algo.monads/maybe-m ?
user=> (macroexpand-1 *1)
(clojure.core/let [name__3075__auto__ m/maybe-m
m-bind (:m-bind name__3075__auto__)
m-result (:m-result name__3075__auto__)
m-zero (:m-zero name__3075__auto__)
m-plus (:m-plus name__3075__auto__)]
(clojure.tools.macro/with-symbol-macros
(m-bind 2 (fn [x]
(m-bind 3 (fn [y]
(m-result (* x y))))))))

21. clojure.algo.monads/maybe-m
just a keyword-function Map
user=> clojure.algo.monads/maybe-m
{:m-zero nil,
:m-plus #object[clojure.algo.monads$fn__3167$m_plus_maybe__3172 0x77a7
:m-result #object[clojure.algo.monads$fn__3167$m_result_maybe__3168 0x
:m-bind #object[clojure.algo.monads$fn__3167$m_bind_maybe__3170 0x142d
user=> (class clojure.algo.monads/maybe-m)
clojure.lang.PersistentArrayMap

22. strategy in algo.monads
1. :m-bind, :m-result をkey、対応する関数を
valueとしたMapを⽤意
2. マクロによってMapから取り出した関数 m-bind,
m-result の組み合わせに変換

23. anatomy of cats
user=> (require '[cats.core :as m]
#_=> '[cats.monad.maybe :as maybe])
nil
user=> (m/mlet [x (maybe/just 2)
#_=> y (maybe/just 3)]
#_=> (m/return (* x y)))
#<Just 6>

24. macroexpand-1
cats.core/bind ?
without explicit monad context?
user=> (macroexpand-1
#_=> '(m/mlet [x (maybe/just 2)
#_=> y (maybe/just 3)]
#_=> (m/return (* x y))))
(cats.core/bind (maybe/just 2) (clojure.core/fn [x]
(cats.core/bind (maybe/just 3) (clojure.core/fn [y]
(do (m/return (* x y)))))))

25. cats.core/bind
cats.context/infer ?
can infer monad context?
user=> (source cats.core/bind)
(defn bind
;; (docstring here)
[mv f]
(let [ctx (ctx/infer mv)]
(p/-mbind ctx mv (fn [v]
(ctx/with-context ctx
(f v))))))
nil

26. cats.context/infer
cats.protocols/Contextual ?
user=> (source cats.context/infer)
(defn infer
;; (docstring here)
;; (0-arity pattern here)
([v]
(cond ; blank lines omitted
(not (nil? *context*))
*context*
(satisfies? p/Contextual v)
(p/-get-context v)
:else
(throw-illegal-argument
(str "No context is set and it can not be automatically "
"resolved from provided value")))))
nil

27. cats.protocols/Contextual
-get-context method
user=> (source cats.protocols/Contextual)
(defprotocol Contextual
"Abstraction that establishes a concrete type as a member of a contex
A great example is the Maybe monad type Just. It implements
this abstraction to establish that Just is part of
the Maybe monad."
(-get-context [_] "Get the context associated with the type."))
nil

28. cats.core/bind (again)
cats.protocols/-mbind ?
user=> (source cats.core/bind)
(defn bind
;; (docstring here)
[mv f]
(let [ctx (ctx/infer mv)]
(p/-mbind ctx mv (fn [v]
(ctx/with-context ctx
(f v))))))
nil

29. cats.protocols/Monad
-mreturn & -mbind methods
user=> (source cats.protocols/Monad))
(defprotocol Monad
"The Monad abstraction."
(-mreturn [m v])
(-mbind [m mv f]))
nil

30. cats.core/bind ( nally)
cats.context/with-context ?
user=> (source cats.core/bind)
(defn bind
;; (docstring here)
[mv f]
(let [ctx (ctx/infer mv)]
(p/-mbind ctx mv (fn [v]
(ctx/with-context ctx
(f v))))))
nil

31. cats.context/with-context
dynamic Var *context*
user=> (source cats.context/with-context)
(defmacro with-context
"Set current context to specific monad."
[ctx & body]
`(do
(when-not (context? ~ctx)
(throw-illegal-argument
"The provided context does not implements Context."))
(binding [*context* ~ctx]
~@body)))
nil
user=> (source cats.context/*context*)
(def ^:dynamic *context* nil)
nil

32. strategy in cats
1. Monad プロトコル(-mreturn, -mbind)を実装した
コンテキストオブジェクトを⽤意
2. Monad 値は Contextual プロトコルによってコン
テキストオブジェクトを取り出せる
3. マクロで関数 bind, return の組み合わせに変換
4. bind は第1引数の Monad 値からコンテキストオブ
ジェクトを取り出す(コンテキストの推論)
5. with-context で⼀度推論したコンテキストオブ
ジェクトを動的スコープで再利⽤

33. Examples

34. example code repositories
cf.
lagenorhynque/mp-in-clojure
lagenorhynque/mp-in-haskell

35. using monads:
safe RPN calculator
from Learn You a Haskell for Great Good!
10.1 Reverse Polish Notation Calculator
14.6 Making a Safe RPN Calculator

36. RPN: reverse Polish notation
↓ with parentheses
↓ evaluate
8 6 1 - * 2 +
((8 (6 1 -) *) 2 +)
42

37. without monads
naïve implementation
(defn- folding-function [[x y & ys :as xs] s]
(cond
(and x y (= s "*")) (conj ys (* y x))
(and x y (= s "+")) (conj ys (+ y x))
(and x y (= s "-")) (conj ys (- y x))
:else (conj xs (Double/parseDouble s))))
(defn solve-rpn [s]
(as-> s v
(str/split v #"s+")
(reduce folding-function () v)
(first v)))

38. ;; valid RPN
user=> (solve-rpn "8 6 1 - * 2 +")
42.0
;; unsupported operator
user=> (solve-rpn "8 6 1 - * 2 /")
NumberFormatException For input string: "/" sun.misc.FloatingDecimal.r
;; invalid number
user=> (solve-rpn "8 6 1 - * a +")
NumberFormatException For input string: "a" sun.misc.FloatingDecimal.r
;; invalid RPN
user=> (solve-rpn "8 6 1 - * 2")
2.0

39. with Maybe monad
valid ⇒ just x ; invalid ⇒ nothing
lift-m for lifting conj function
(defn- read-maybe [s]
(try
(maybe/just (Double/parseDouble s))
(catch NumberFormatException _
(maybe/nothing))))
(defn- folding-function' [[x y & ys :as xs] s]
(cond
(and x y (= s "*")) (maybe/just (conj ys (* y x)))
(and x y (= s "+")) (maybe/just (conj ys (+ y x)))
(and x y (= s "-")) (maybe/just (conj ys (- y x)))
:else ((m/lift-m 1 #(conj xs %))
(read-maybe s))))

40. reduce with monadic function using foldm
length of result sequence ≠ 1 ⇒ nothing
MonadZero
cf. MonadPlus, Alternative
(defn solve-rpn' [s]
(m/mlet [result (m/foldm folding-function'
()
(str/split s #"s+"))
:when (= (count result) 1)]
(m/return (first result))))

41. ;; valid RPN
user=> (solve-rpn' "8 6 1 - * 2 +")
#<Just 42.0>
;; unsupported operator
user=> (solve-rpn' "8 6 1 - * 2 /")
#<Nothing>
;; invalid number
user=> (solve-rpn' "8 6 1 - * a +")
#<Nothing>
;; invalid RPN
user=> (solve-rpn' "8 6 1 - * 2")
#<Nothing>

42. making monads:
probability distribution
from Learn You a Haskell for Great Good!
14.8 Making Monads

43. probability distribution
e.g. 6-sided die
n p
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6

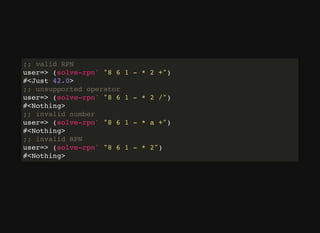
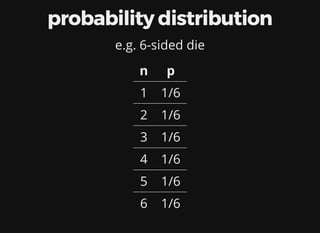
44. implementing Prob monad
define the data type Prob
(deftype Prob [v]
p/Contextual
(-get-context [_] context)
p/Extract
(-extract [_] v)
p/Printable
(-repr [_]
(str "#<Prob " (pr-str v) ">"))
Object
(equals [this obj]
(= (.v this) (.v obj))))

45. define the context object for Prob
(def context
(reify
;; (other protocol implementations here)
p/Monad
(-mreturn [m v]
(p/-pure m v))
(-mbind [_ mv f]
(assert (prob? mv)
(str "Context mismatch: " (p/-repr mv)
" is not allowed to use with prob context."))
(->Prob (for [[x p] (p/-extract mv)
[y q] (p/-extract (f x))]
[y (* p q)])))
;; (below omitted)

46. define factory/conversion functions
(defn uniform [s] ; sequence
(let [n (count s)] ; -> Prob value of uniform distribution
(->> s
(map (fn [x] [x (/ 1 n)]))
->Prob)))
(defn prob->dist [prob] ; Prob value -> Map of distribution
(letfn [(add-prob [d [x p]]
(update d x (fnil #(+ % p) 0)))]
(reduce add-prob {} (p/-extract prob))))

47. sum of 2 dice
user=> (def die (range 1 (inc 6)))
#'user/die
user=> (def prob
#_=> (m/mlet [d1 (uniform die)
#_=> d2 (uniform die)]
#_=> (m/return (+ d1 d2))))
#'user/prob
user=> prob
#<Prob ([2 1/36] [3 1/36] [4 1/36] [5 1/36] [6 1/36] [7 1/36] [3 1/36]
user=> (prob->dist prob)
{7 1/6, 4 1/12, 6 5/36, 3 1/18, 12 1/36, 2 1/36, 11 1/18,
9 1/9, 5 1/9, 10 1/12, 8 5/36}

48. Monty Hall problem
user=> (def doors #{:a :b :c})
#'user/doors
user=> (prob->dist
#_=> (m/mlet [prize (uniform doors)
#_=> choice (uniform doors)]
#_=> (m/return (if (= choice prize)
#_=> :win
#_=> :lose))))
{:win 1/3, :lose 2/3}

49. user=> (prob->dist
#_=> (m/mlet [prize (uniform doors)
#_=> choice (uniform doors)
#_=> opened (uniform (disj doors prize choice))
#_=> choice' (uniform (disj doors opened choice))]
#_=> (m/return (if (= choice' prize)
#_=> :win
#_=> :lose))))
{:lose 1/3, :win 2/3}

50. Vive les S-expressions !
Long live S-expressions!

51. Further Reading
/
/
clojure/algo.monads
khinsen/monads-in-clojure
funcool/cats
独習 Scalaz learning Scalaz
猫番 herding cats
モナド (プログラミング) - Wikipedia

52. /
第14章 もうちょっとだけモナド / For a Few
Monads More
10.1 逆ポーランド記法電卓 /
14.6 安全な逆ポーランド記法電卓を作ろう /
Making a Safe RPN Calculator
14.8 モナドを作る /
『すごいHaskellたのしく学ぼう！』 Learn You a
Haskell for Great Good!
Reverse Polish
Notation Calculator
Making Monads

53. cf.
Haskell の Monad とは⾔語内DSLのフレームワー
クである
Functor, Applicative, Monadのシンプルな定式化
継承によらないポリモーフィズム実現⼿法
思ったほど怖くない！ Haskell on JVM 超⼊⾨
MP in Scala
MP in Haskell
Free Monads Getting Started