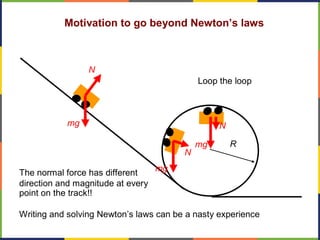
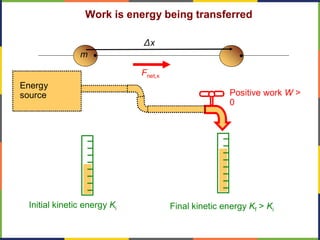
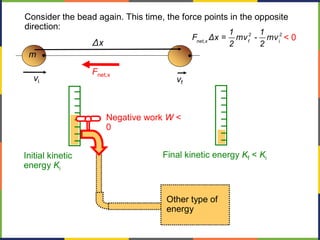
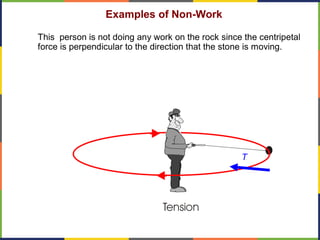
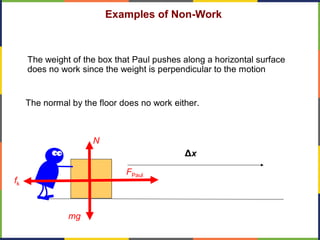
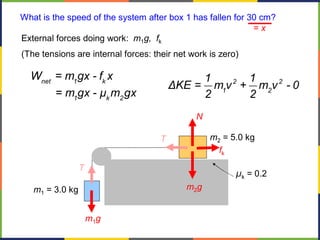
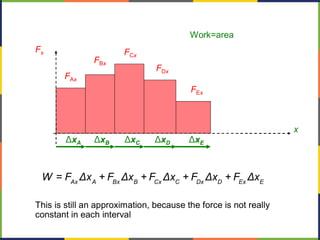
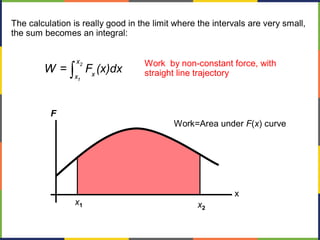
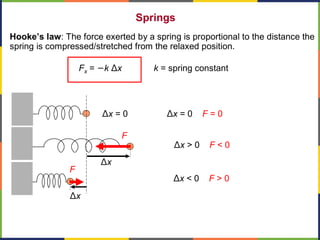
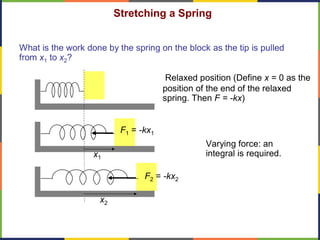
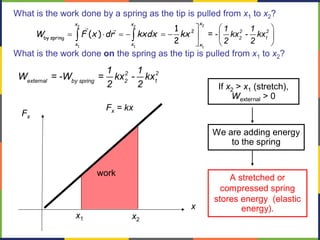
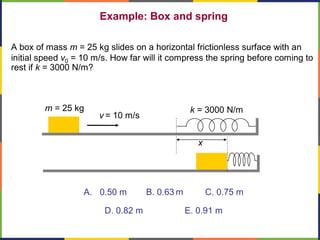
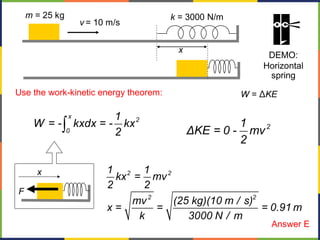
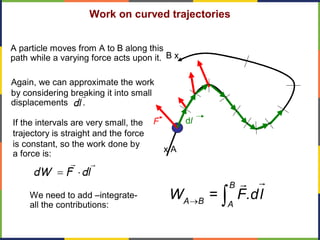
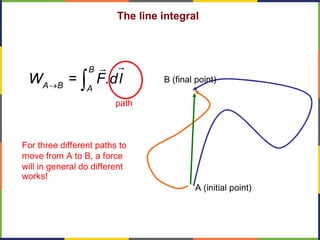
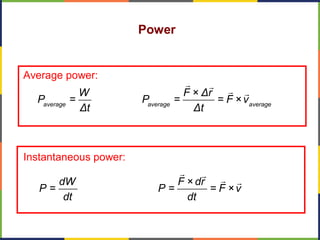
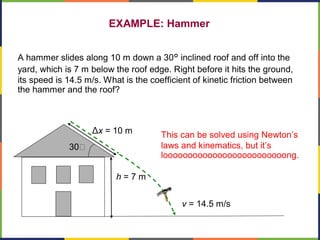
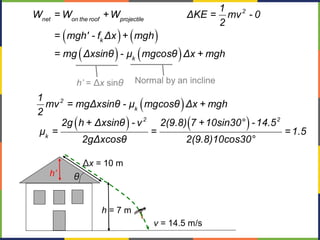
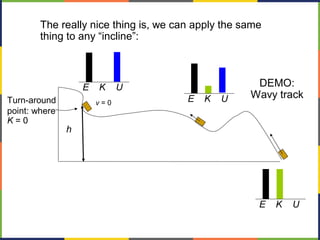
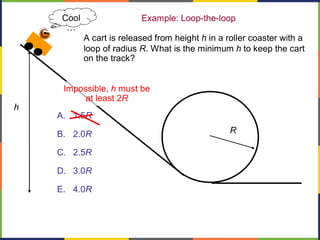
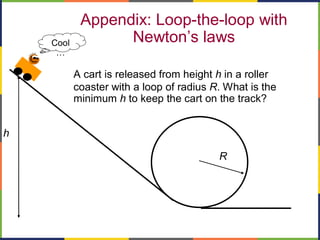
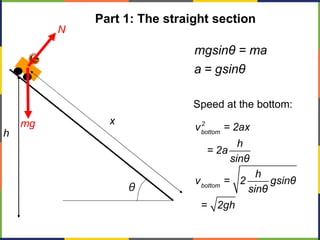
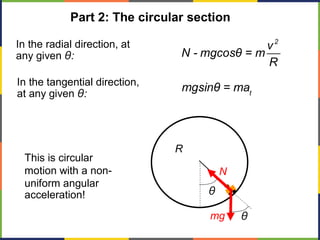
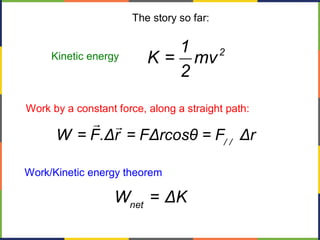
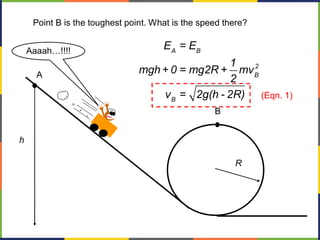
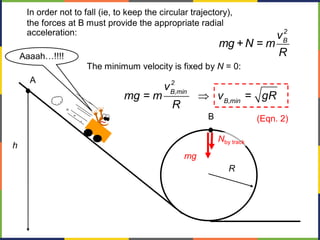
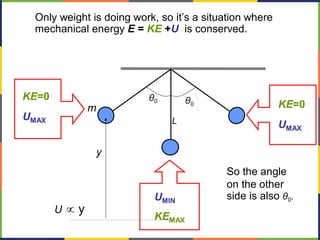
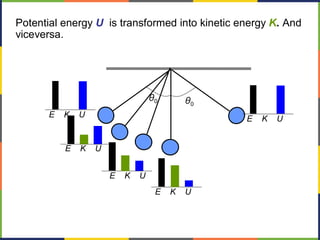
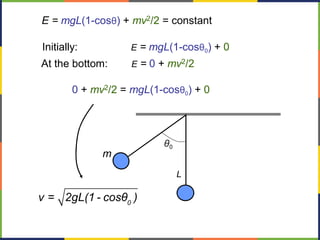
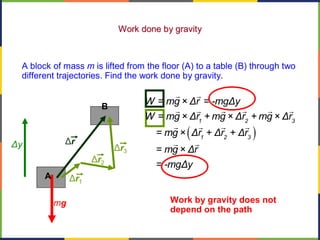
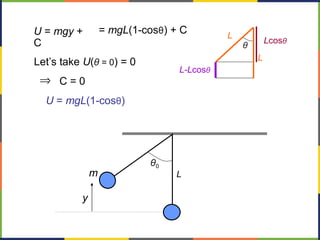
1. The document discusses work, energy, and their relationship as described by the work-energy theorem. It defines work as a force applied over a displacement, and gives the equation W=Fd. 2. Kinetic energy is defined as K=1/2mv^2. The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy, or W=ΔK. 3. Potential energy, such as gravitational potential energy mgh, is discussed. The work done by gravity in lifting an object does not depend on the path, only the change in height.

1. COLLEGE PHYSICS
Chapter 7 – WORK & ENERGY

2. Motivation to go beyond Newton’s laws
Loop the loop
R
mg
N
mg
N
mg
N
The normal force has different
direction and magnitude at every
point on the track!!
Writing and solving Newton’s laws can be a nasty experience

3. Playing around with Newton’s 2nd law.
Consider the motion of a bead of mass m on a straight wire pushed by
a constant net force Fx parallel to the wire, along a displacement Δx:
Fnet,x
m
Δx
x x
F = m aForce produces
acceleration:
2 2
x f i
2a Δx = v - v
vi vf
Acceleration produces
change in speed:
2 2x
f i
F
2 Δx = v - v
m
Change in
KINETIC ENERGY
(K) of the bead
2 2
net,x f i
1 1
F Δ x = m v - m v
2 2
WORK (W ) done
by force F over
displacement Δx

4. This is an expression of the “effectiveness” of the force.
net
W = ΔK
Of how a force applied
over a distance…
…changes something in the
system
Work
The “external agent” that
changes the amount of kinetic
energy (the state) in the system
x
W = F Δ x
Kinetic energy
The “internal” quantity (state)
of the system
21
K = mv
2
2 2
net,x f i
1 1
F Δx = mv - mv
2 2
Work/Kinetic Energy Theorem

5. m
Δx
Initial kinetic energy Ki Final kinetic energy Kf > Ki
Positive work W >
0
Energy
source
Work is energy being transferred
Fnet,x

6. Units for work and energy:
SI:
Not to be confused with:
Calorie (or food calorie) 1 Cal = 1000 cal
calorie 1 cal = 4.184 J
Kilowatt-hour KWh
Other common units:
Joule 1 J = 1 N · m

7. Energy
Many types of energy:
• kinetic energy
• electric energy
• internal –thermal- energy
• elastic energy
• chemical energy
• Etc.
Energy is transferred and
transformed from one type
to another and is never
destroyed or created.

8. What is work?
The definition of work W =F Δx corresponds to the intuitive idea of
effort:
• More massive object will require more work to get to the same
speed (from rest)
• For a given mass, getting to a higher speed (from rest) requires
more work
• If we push for a longer distance, it’s more work.
• It takes the same work to accelerate the object to the right as to
the left (both displacement and force reverse)

9. Other type of
energy
2 2
net,x f i
1 1
F Δx = mv - mv
2 2
Consider the bead again. This time, the force points in the opposite
direction:
m
Δx
vi vf
< 0
Initial kinetic
energy Ki
Final kinetic energy Kf < Ki
Negative work W <
0
Fnet,x

10. Example: Pushing a box with friction
Paul pushes a box along 10 m across the floor at a constant velocity
by exerting a force of 200N.
Work by Paul on the box: WPaul = (200 N)(10 m) = 2000 J
(energy coming from the biochemical reactions in his muscles)
Work by friction on the box: Wf = (-200 N)(10 m) = -2000 J
(released as thermal energy into the air and the floor)
FPaul
f
k
Paul k
k Paul
F - f = ma = 0 (constant speed)
f = F
WKE theorem: WPaul + Wf = 0 Kf – Ki = 0 

11. Example: Free fall with WKE
2
W = ΔK
1
mgh = mv
2
A ball is dropped and hits the ground 50 m below. If the initial speed is 0 and
we ignore air resistance, what is the speed of the ball as it hits the ground?
Change in K: 2
final initial
1
ΔK = K - K = m v - 0
2
We can use kinematics or… the WKE theorem.
Work done by gravity: mgh
mg
Δr
2
v = 2gh = 2(9.8 m / s )(50 m) = 31m / s
A. 50 m/s
B. 42 m/s
C. 31 m/s
D. 23 m/s
E. 10 m/s

12. Examples of Non-Work
This person is not doing any work on the rock since the centripetal
force is perpendicular to the direction that the stone is moving.
T

13. Examples of Non-Work
FPaul
fk
mg
N
The weight of the box that Paul pushes along a horizontal surface
does no work since the weight is perpendicular to the motion
The normal by the floor does no work either.
Δx

14. Example: Systems with several objects
μk = 0.2
m2 = 5.0 kg
m1 = 3.0 kg
What is the speed of the system after box 1 has fallen for 30 cm?
Two approaches:
1. Use Newton’s laws to find acceleration; use
kinematics to find speed. (long!!)
2. Use WKE theorem (smart!)

15. μk = 0.2
m2 = 5.0 kg
m1 = 3.0 kg
What is the speed of the system after box 1 has fallen for 30 cm?
External forces doing work: m1g, fk
(The tensions are internal forces: their net work is zero)
net 1 k
W = m gx - f x
m1g
m2g
N
fk
T
T
= x
1 k 2
= m gx - μ m gx
2 2
1 2
1 1
ΔKE = m v + m v - 0
2 2

16. ( ) ( ) 2
1 k 2 1 2
1
m - μ m gx = m + m v
2
1 k 2
1 2
m - μ m
v = 2gx
m + m
m1 = 3.0 kg
m2 = 5.0 kg
μk = 0.2
x = 0.3 m
3 - 0.2 × 5
= 2(9.8)(0.3) =1.2 m / s
3 + 5

17. Work: Varying forces and
curved trajectories
Power

18. The story so far:
net
W = ΔK
Kinetic energy 21
K = mv
2
/ /
W = F.Δr = FΔrcosθ = F Δr
r r
Work by a constant force, along a straight path:
Work/Kinetic energy theorem

19. The journey is divided up into a series of segments over which the force is
constant.
Work by non-constant force, with straight line trajectory
An object moves along the x-axis from point x1 to x2. A non-constant force
is applied on the object. What is the work done by this force?
x1
FA
ΔxA
FB
ΔxB
FC
ΔxC
FD
ΔxD
FE
ΔxE
Ax A Bx B Cx C Dx D Ex E
W = F Δx + F Δx + F Δx + F Δx + F Δx
The total work is the sum of the works for each of the intervals:
x2

20. Fx
x
ΔxA ΔxB ΔxC ΔxD ΔxE
Work=area
FAx
FBx
FCx
FDx
FEx
This is still an approximation, because the force is not really
constant in each interval
Ax A Bx B Cx C Dx D Ex E
W = F Δx + F Δx + F Δx + F Δx + F Δx

21. F
x
Work=Area under F(x) curve
x1 x2
The calculation is really good in the limit where the intervals are very small,
the sum becomes an integral:
ò
2
1
x
xx
W = F (x)dx
Work by non-constant force, with
straight line trajectory

22. Springs
Hooke’s law: The force exerted by a spring is proportional to the distance the
spring is compressed/stretched from the relaxed position.
Δx = 0 Δx = 0 F = 0
Fx = −k Δx k = spring constant
Δx
Δx > 0 F < 0
F
Δx
Δx < 0 F > 0
F

23. Stretching a Spring
What is the work done by the spring on the block as the tip is pulled
from x1 to x2?
Relaxed position (Define x = 0 as the
position of the end of the relaxed
spring. Then F = -kx)
F1 = -kx1
x1
x2
F2 = -kx2
Varying force: an
integral is required.

24. 22 2
1 1 1
2
by spring
1
( )
2
xx x
x x x
W F x dr kxdx kx
ù æ ö
= × = - = - ç ÷ú
û è ø
ò ò
2 2
2 1
1 1
= - kx - kx
2 2
r r
What is the work done by a spring as the tip is pulled from x1 to x2?
Fx
x
x1 x2
work
Fx = kx
If x2 > x1 (stretch),
Wexternal > 0
We are adding energy
to the spring
A stretched or
compressed spring
stores energy (elastic
energy).
2 2
external by spring 2 1
1 1
W = -W = kx - kx
2 2
What is the work done on the spring as the tip is pulled from x1 to x2?

25. Example: Box and spring
A box of mass m = 25 kg slides on a horizontal frictionless surface with an
initial speed v0 = 10 m/s. How far will it compress the spring before coming to
rest if k = 3000 N/m?
A. 0.50 m B. 0.63 m C. 0.75 m
D. 0.82 m E. 0.91 m
x
v = 10 m/s
m = 25 kg k = 3000 N/m

26. W = ΔKE
2 2
2 2
1 1
kx = mv
2 2
mv (25 kg)(10 m / s)
x = = = 0.91 m
k 3000 N / m
F
x
ò
x
2
0
1
W = - kxdx = - kx
2
Use the work-kinetic energy theorem:
21
ΔKE = 0 - mv
2
x
v = 10 m/s
m = 25 kg k = 3000 N/m
DEMO:
Horizontal
spring
Answer E

27. Work on curved trajectories
A particle moves from A to B along this
path while a varying force acts upon it.
l
rr
dFdW ×=
If the intervals are very small, the
trajectory is straight and the force
is constant, so the work done by
a force is:
Again, we can approximate the work
by considering breaking it into small
displacements .l
r
d
We need to add –integrate-
all the contributions: ® ò
B
A B A
W = F.dl
rr
x A
B x
F dl

28. The line integral
A (initial point)
B (final point)
For three different paths to
move from A to B, a force
will in general do different
works!
path
® ò
B
A B A
W = F.dl
rr

29. rim
bottom
mg
θ
θ
Example: Spherical bowl
Find the work done by gravity on a pebble of mass m as it rolls from the
rim to the bottom of a spherical bowl of radius R.
dl
ò
ò
ò
bottom
top
θ=π / 2
θ=0
π / 2
0
π / 2
0
W = mg × dl
= mg Rdθ cosθ
= mgR cosθ dθ
= mgR sinθ
= mgR
rr
= R dθ

30. Power
Instantaneous power:
dW F × dr
P = P = = F × v
dt dt
r r r r
average average average
W F × Δr
P = P = = F × v
Δt Δt
r r r r
Average power:

31. Units of power
SI: Watt 1 W = 1 J/s
Other: Horsepower 1 hp = 746 W
Kilowatt-hour (kWh) is a unit of energy or work:
61000 W 3600 s
1 kWh =1 kW × h = 3.6 ×10 Ws
1 kW 1 h
J

32. Example: Bullet and wood block
A bullet of mass 10–3 kg traveling at a speed of 300 m/s strikes a
block of wood. It embeds a distance of 1 cm. How much force does
the wood exert on the bullet as it slows it down?
Identify
Let us assume that the force is constant (or that we will find the
average force)
The force must do enough negative work on the bullet to render
its kinetic energy 0.

33. f i
2
2
i
f i i
W = ΔK
FΔx = K - K
1
0 - mvK - K mv2F = = = -
Δx Δx 2Δx
WKE theorem:Setup
Execute
2 -3 2
i
-2
mv (10 kg)(300 m / s)
F = - = - = -4500 N
2Δx 2(10 m)
The wood exerts a force of –4500N on the bullet. It should be
negative (opposite to Δx) because it must decelerate the bullet.
Evaluate

34. EXAMPLE: Hammer
A hammer slides along 10 m down a 30° inclined roof and off into the
yard, which is 7 m below the roof edge. Right before it hits the ground,
its speed is 14.5 m/s. What is the coefficient of kinetic friction between
the hammer and the roof?
Δx = 10 m
h = 7 m
v = 14.5 m/s
30
This can be solved using Newton’s
laws and kinematics, but it’s
looooooooooooooooooooooooong.

35. ( ) ( )
( ) ( )
2
net on the roof projectile
k
k
1
W = W + W ΔKE = mv - 0
2
= mgh' - f Δx + mgh
= mg Δxsinθ - μ mgcosθ Δx + mgh
Δx = 10 m
h = 7 m
v = 14.5 m/s
h’ θ
Normal by an inclineh’ = Δx sinθ
( )2
k
1
mv = mgΔxsinθ - μ mgcosθ Δx + mgh
2
( ) ( )2 2
k
2g h + Δxsinθ - v 2(9.8) 7 +10sin30° -14.5
μ = = =1.5
2gΔxcosθ 2(9.8)10cos30°

36. Energy Conservation; Potential Energy

37. Work done by gravityWork done by gravity
A block of mass m is lifted from the floor (A) to a table (B) through two
different trajectories. Find the work done by gravity.
Δy
mg
A
B
Δr3
Δr2
Δr1
Δr
( )
1 2 3
1 2 3
W = mg × Δr = -mgΔy
W = mg × Δr + mg × Δr + mg × Δr
= mg × Δr + Δr + Δr
= mg × Δr
= -mgΔy
r r
r r r r r r
r r r r
r r
Work by gravity does not
depend on the path

38. Gravitational potential energy
The work done by gravity does not depend on the path, it only depends on
the vertical displacement Δy, or on the initial and final y:
W = -mgΔy
U = potential energy
We can ALWAYS write this work as (minus) the change in some function
U(r) that depends on position (not on path):
( )f i
W = - U - U = -ΔU
U = mgy + constantGravitational potential energy:
There is always room for an arbitrary constant,
because what matters is ΔU

39. Can work always be written in terms of a potential
energy change?
NO!
Example: A box is dragged along a rough horizontal surface
through two paths AD and ABCD:
A
B C
D
friction,AD k
W = -df
The work done by friction CANNOT
be written as a potential difference.
Does not depend
on initial and final
points only.
friction,ABCD k
W = -3df

40. Conservative and non-conservative forces
The work done by a conservative force does not depend on
the trajectory.
• A potential energy function can be defined.
• The work done by a non-conservative force depends on the
trajectory.
• A potential energy function cannot be defined.
Non-conservative force = force that is not conservative.
Examples: Kinetic friction
Examples: Gravity, spring

41. Conservation of Mechanical Energy
In a system where only conservative forces are doing work, we can
rewrite the WKE theorem:
KW D=net
UW D-=net
KU D=D- 0)( =+D UK
Definition of Mechanical Energy: UKE +=
Under the conditions above,
mechanical energy is conserved:
finalinitial
or0 EEE ==D

42. 2
W = ΔK
1
mgh = mv
2
v = 2gh
A ball is dropped from a height h. If the initial speed is 0 and we ignore air
resistance, what is the speed of the ball as it hits the ground?
We can use kinematics or… the WKE theorem… or conservation of energy.
Work done by
gravity: mgh
mg
Δr
initial final
initial initial final final
2
2
E = E
K +U = K + U
1
0 + mgh = mv + 0
2
1
mgh = mv
2
v = 2gh
The only force doing work is gravity, so
mechanical energy is conserved.
Choice: U = 0
at ground level
WKE Conservation of energy
Example: Free fall

43. Two ways of looking at the same problem.
1. Lifting: Wnet = Wgravity + Wperson = 0 (vinitial = vfinal = 0)
Drop: Wnet =Wgravity = mgh > 0 (thus K increases)
An object of mass m is lifted by a person from the floor to
height h and dropped.
1. Lifting: Wperson > 0. Person is adding energy which is
stored as gravitational potential energy mgh > 0 .
Drop: The potential energy is converted into kinetic
energy (thus K increases)

44. The really nice thing is, we can apply the same
thing to any “incline”:
h
Turn-around
point: where
K = 0
E K U
DEMO:
Wavy trackE K U
E K U
v = 0

45. Example: Loop-the-loop
A. 1.5R
B. 2.0R
C. 2.5R
D. 3.0R
E. 4.0R
A cart is released from height h in a roller coaster with a
loop of radius R. What is the minimum h to keep the cart
on the track?
h
R
Impossible, h must be
at least 2R
Cool
…

46. h
R
Aaaah…!!!!
A
B
Point B is the toughest point. What is the speed there?
(Eqn. 1)
A B
2
B
B
E = E
1
mgh+ 0 = mg2R + mv
2
v = 2g(h - 2R)

47. h
R
Aaaah…!!!!
A
B
In order not to fall (ie, to keep the circular trajectory),
the forces at B must provide the appropriate radial
acceleration: 2
B
v
mg + N = m
R
mg
Nby track
The minimum velocity is fixed by N = 0:
Þ
2
B,min
B,min
v
mg = m v = gR
R
(Eqn. 2)

48. Let us put equations 1 and 2 together:
B B,min
v = 2g(h - 2R) v = gR
The minimum height is given by:
min
gR = 2g(h - 2R)
min
min
R = 2h - 4R
5
h = R
2
Answer C

49. Appendix: Loop-the-loop with
Newton’s laws
A cart is released from height h in a roller
coaster with a loop of radius R. What is the
minimum h to keep the cart on the track?
h
R
Cool
…

50. h
mg
N
Part 1: The straight section
mgsinθ = ma
a = gsinθ
θ
x
Speed at the bottom:
2
bottom
bottom
v = 2ax
h
= 2a
sinθ
h
v = 2 gsinθ
sinθ
= 2gh

51. R
Part 2: The circular section
mg
N
θ
θ
In the radial direction, at
any given θ:
2
v
N - mgcosθ = m
R
In the tangential direction,
at any given θ: t
mgsinθ = ma
This is circular
motion with a non-
uniform angular
acceleration!

52. 2
N - mgcosθ = mRω
gsinθ = Rα
In terms of angular quantities:
æ ö
ç ÷
è ø
2
dθ
N - mgcosθ = mR
dt2
2
d θ
gsinθ = R
dt
Differential equations for θ (at
least not coupled)
(1)
(2)

53. dω g
ω = sinθ
dθ R
2
2
d θ dω dω dθ dω
On equation (2),use this trick : = = = ω
dt dθ dt dθdt
g
ω dω = sinθdθ
R
( ) ( )2 2
0
1 g
ω - ω = cosθ - cos0°
2 R
where ω0 is the angular speed
at the bottom, see part 1:
bottom
0
v 2gh
ω = =
R R
( )
æ ö
ç ÷
è ø
2
2
2gh 2g 2g h
ω = + cosθ -1 = + cosθ -1
R R RR
integrate
(now it’s a first order differential
equation)

54. At the top, θ = 180º:
æ ö
ç ÷
è ø
2
top
2g h
ω = - 2
R R
From equation (1), and for θ = 180º:
2
top
N + mg = mRω
Minimum speed ⇒ N = 0
2
top,min
mg = mRω
(3)
(4)
(3) and (4):
æ ö
ç ÷
è ø
min
h2g g
- 2 =
R R R m in
5
h = R
2

55. EXAMPLE: Pendulum
Consider a pendulum of length l and mass m, that is released
from rest at an angle θ0.
a. What is the maximum angle that the pendulum will reach
on the other side?
b. What is the maximum speed of the pendulum?
θ0
m l

56. Only weight is doing work, so it’s a situation where
mechanical energy E = KE +U is conserved.
L
m
θ0
U µ y
y
KE=0
UMAX
UMIN
KEMAX
θ0 KE=0
UMAX
So the angle
on the other
side is also θ0.

57. θ0 θ0
E K U E K U
E K U
E K U
E K U
Potential energy U is transformed into kinetic energy K. And
viceversa.

58. θ0
m L
Let’s take U(θ = 0) = 0
⇒ C = 0
U = mgL(1-cosθ)
U = mgy +
C
y
Lcosθ
= mgL(1-cosθ) + C
θ
L
L
L-Lcosθ

59. θ0
m
L
E = mgL(1-cosθ) + mv2/2 = constant
At the bottom: E = 0 + mv2/2
Initially: E = mgL(1-cosθ0) + 0
0 + mv2/2 = mgL(1-cosθ0) + 0
0
v = 2gL(1 - cosθ )