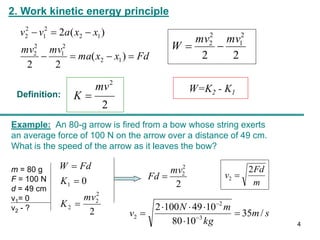
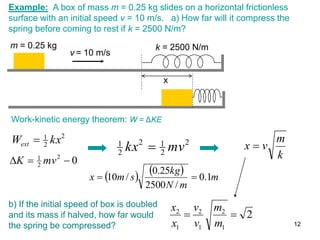
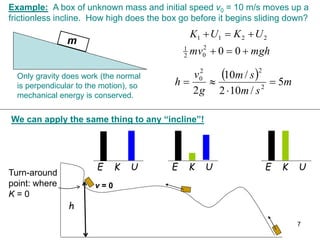
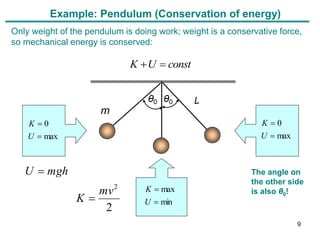
1. Work done by a constant force depends on the magnitude of the force and the displacement along the direction of the force. Work done by opposing forces is negative. Centripetal forces do no work as they are always perpendicular to motion. 2. The work-kinetic energy theorem states that the work done on an object equals its change in kinetic energy. It can be used to calculate changes in speed. 3. Gravitational potential energy is defined as mgh. The principle of conservation of mechanical energy can be used to solve problems involving changes in kinetic and potential energy in an isolated system, such as an object moving under gravity.

1. Work and energy
1. Work done by a constant force
Definition:
1a. Positive and negative work
[W] = N*m = J
Work done by forces that oppose the
direction of motion will be negative.
d
F
Fd
d
F
W




 
cos
||
Centripetal forces do no work, as
they are always perpendicular to the
direction of motion.
Units:
1

2. F
x
F
y
F
x
y
f

m
5
a
Example: An object of unknown mass is displaced 5 m by a constant
force F = 20 N as shown below (angle θ=60º). Force of friction is f = 6 N.
Find the work done by each of these forces and the total work.
    J
m
N
N
x
f
F
W
J
m
N
fx
x
f
W
J
m
N
x
F
x
F
W
tot
fr
x
F
20
)
5
(
6
60
cos
20
cos
30
)
5
)(
6
(
)
180
(cos
50
)
5
)(
60
)(cos
20
(
)
cos
(
0
0
0


















Find mass of the object if the coefficient of kinetic friction is 0.5. 2

3. A. Positive
B. Negative
C. Zero
Example: A block slides down a rough inclined surface. The forces acting
on the block are depicted below. The work done by the frictional force is:
Wf = |fk| |Δx| cos(180°) = -|fk| |Δx| < 0
Work done by the normal force: WN = |N| |Δx| cos(90°) = 0
Work done by weight: Wmg = |mg| |Δx| cos(θ ) > 0
0 < θ < 90°
N
mg
y
x
f

3

4. 2. Work kinetic energy principle
Fd
x
x
ma
mv
mv
x
x
a
v
v







)
(
2
2
)
(
2
1
2
2
1
2
2
1
2
2
1
2
2
2
2
2
1
2
2 mv
mv
W 

2
2
mv
K 
Definition:
W=K2 - K1
Example: An 80-g arrow is fired from a bow whose string exerts
an average force of 100 N on the arrow over a distance of 49 cm.
What is the speed of the arrow as it leaves the bow?
m = 80 g
F = 100 N
d = 49 cm
v1= 0
v2 - ? 2
0
2
2
2
1
mv
K
K
Fd
W



2
2
2
mv
Fd 
m
Fd
v
2
2 
s
m
kg
m
N
v /
35
10
80
10
49
100
2
3
2
2 




 

4

5. Example: Two blocks (m1=2m2) are pushed by identical forces, each
starting at rest at the same start line. Which object has the greater kinetic
energy when it reaches the same finish line?
Same force, same distance Same work
Same change in kinetic energy
1. Box1
2. Box 2
3. They both have the
same kinetic energy
Example: A ball is dropped and hits the ground 50 m below. If the initial
speed is 0 and we ignore air resistance, what is the speed of the ball as it
hits the ground?
We can use kinematics or… the WKE theorem
2
v = 2gh = 2(9.8 m / s )(50 m) = 31m / s
Work done by gravity: mgh
0
2
2
1




 mv
mgh
K
W
5

6. 3.Gravitational potential energy. Conservation of energy
h
1
2
)
(
2
2
1
2
1
2
1
2
2
1
2
2
U
U
K
K
)
h
mg(h
mgh
U
W
mv
mv














W
U 


Definition:
mgh
Ug 

)
( 1
2 h
h
mg
mgh
W
mg
F
g
g







const
E
U
K
U
K 



 2
2
1
1
0





 E
U
K
For closed isolated system
Conservation of mechanical energy:
6

7. Example: A box of unknown mass and initial speed v0 = 10 m/s moves up a
frictionless incline. How high does the box go before it begins sliding down?
m
mgh
mv 

 0
0
2
0
2
1
2
2
1
1 U
K
U
K 


  m
s
m
s
m
g
v
h 5
/
10
2
/
10
2 2
2
2
0




Only gravity does work (the normal
is perpendicular to the motion), so
mechanical energy is conserved.
We can apply the same thing to any “incline”!
h
Turn-around
point: where
K = 0
E K U
E K U
E K U
v = 0
7

8. mgh
Uinitial 
h
final
initial E
E 
2
2
mv
mgh 
gh
v 2

2
2
mv
K final 
Example: A roller coaster starts out at the top of a hill of height h.
How fast is it going when it reaches the bottom?
Example: An object of unknown mass is projected with an initial speed,
v0 = 10 m/s at an unknown angle above the horizontal. If air resistance
could be neglected, what would be the speed of the object at height,
h = 3.3 m above the starting point?
?
3
.
3
/
10
0



v
m
h
s
m
v
  s
m
m
s
m
s
m
gh
v
v
mg
mv
mgh
mv
/
0
.
6
3
.
3
/
8
.
9
2
/
10
2
0
2
2
2
2
2
0
2
0
2










8

9. Only weight of the pendulum is doing work; weight is a conservative force,
so mechanical energy is conserved:
L
m
θ0
The angle on
the other side
is also θ0!
θ0
const
U
K 

max
0


U
K
max
0


U
K
2
2
mv
K 
mgh
U 
min
max


U
K
Example: Pendulum (Conservation of energy)
9

10. Example: Pendulum (Conservation of energy)
The pendulum with a mass of 300 g is deviated from the equilibrium position
B to the position A as shown below. Find the speed of the pendulum at the
point B after the pendulum is released.
0

 A
A K
mgh
U
A. Energy of the pendulum at the point A:
B. Energy of the pendulum at the point B:
0

B
U
0
2
0
2






mv
mgh
U
K
U
K B
B
A
A
C. Conservation of energy:
2
2
mv
KB 
s
m
m
s
m
gh
v /
97
.
1
2
.
0
/
8
.
9
2
2 2






cm
h 20

B
A
v
10

11. 4.Hook’s Law (elastic forces)
Fext
Fext
Fext
F
C
kx
U 
 2
2
1
2
2
1
2
2
1
i
f
ext
system
by kx
kx
W
W
U 





kx
F 

Potential energy
11

12. Example: A box of mass m = 0.25 kg slides on a horizontal frictionless
surface with an initial speed v = 10 m/s. a) How far will it compress the
spring before coming to rest if k = 2500 N/m?
x
v = 10 m/s
m = 0.25 kg k = 2500 N/m
Work-kinetic energy theorem: W = ΔKE
2
2
1
kx
Wext 
    m
m
N
kg
s
m
x 1
.
0
/
2500
25
.
0
/
10 

2
2
1
2
2
1
mv
kx 
0
2
2
1


 mv
K k
m
v
x 
b) If the initial speed of box is doubled
and its mass if halved, how far would
the spring be compressed?
2
1
2
1
2
1
2


m
m
v
v
x
x
12

13. 5. Conservative and nonconservative forces
•Forces such as gravity or the elastic force, for which the work does not
depend on the path taken but only on the initial and final position, are called
conservative forces
•For conservative forces work done on a closed path (a lop) is equal to zero
•Friction is a nonconservative force
2
1
3
A
B
Example: A block is moved from rest at point A to rest at point B.
Which path requires the most work to be done on the object?
A) The table is leveled and friction is present.
Path 1. Path 2. Path 3. All the same
B) The table is tilted and frictionless.
Path 1. Path 2. Path 3. All the same
13

14. 6. Power
1W=1J/s
 





t
d
F
P


v
F
v
F
P ||





Horsepower:
1 hp = 746 W
Units:
Definition:
t
W
P



Example: You move 500 kg of bricks 1.0 m up. It takes 30 minutes by hand,
or 10 minutes by lift. What is the power in each case?
J
m)
)(
s
m
.
kg)(
(
Fd
W 4900
0
.
1
8
9
500 2



 
W
.
)
s
(
J
t
W
P
hand
hand 7
2
min
60
min
30
4900





Work is the same:
W
.
P
t
W
P hand
lift
lift 2
8
3 




14

15. Example: Two elevators A and B carry each a load of mass m from the first
floor to the third floor of a building at constant speeds, but A is twice as fast
as B. 1) Compare work done by the cable tension (ie, the energy produced
by the engine). 2) Compare power of two elevators.
T =mg
mg
Δx
t
W
P



B
A
A
B
v
v
t
t
2
2


B
A P
P 2

B
A W
W 


x
mg
W 


1)
2)
15