This document provides an overview of a workshop on computational aspects of game theory held from June 16-20, 2014 at the Indian Statistical Institute Kolkata. The workshop was organized by Raj Dasgupta and covered topics including normal form games, Bayesian games, mechanism design, and coalition games. Students presented on topics from the workshop and worked on programming tools for solving game theory problems.

1. GAMUTGAMUT
WORKSHOP ONWORKSHOP ON COMPUTATIONALCOMPUTATIONAL
ASPECTS OF GAME THEORYASPECTS OF GAME THEORY
J U N E 1 6 - 2 0 , 2 0 1 4
E C S U , I N D I A N S T A T I S T I C A L I N S T I T U T E K O L K A T A
PrithvirajPrithviraj (Raj)(Raj) DasguptaDasgupta
AssociateAssociate Professor, ComputerProfessor, Computer ScienceScience Department,Department,
UniversityUniversity of Nebraska, Omahaof Nebraska, Omaha

2. SPEAKER’S BACKGROUND
• Associate Professor, Computer Science, University of
Nebraska, Omaha (2001- present)
• Director, CMANTIC Lab (robotics, computational
economics)
• Ph.D. (2001) Univ. of California, Santa Barbara• Ph.D. (2001) Univ. of California, Santa Barbara
• Computational economics using software agents
• B.C.S.E (1995) – Jadavpur University
• 1994: Summer internship at I.S.I
June 16-20, 2014 2Game Theory Workshop - Raj Dasgupta

3. UNIVERSITY OF NEBRASKA, OMAHA
• Founded in 1908
• Computer Science
program started in
early 80s
• Department since early
90s90s
• 18 full-time faculty
• ~400 undergrad, 125
Masters and 15 Ph.D.
students
• Research areas: AI,
Database/Data mining,
Networking, Systems
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 3

4. C-MANTIC GROUP
• http://cmantic.unomaha.edu
• Research Topics:
• Multi-robot systems path and task planning
• Multi-robot/agent systems coordination using game
theory-based techniques
• Modular robotic systems, Information aggregation using
prediction markets, Agent-based crowd simulation, etc.prediction markets, Agent-based crowd simulation, etc.
• Established by Raj Dasgupta in 2004
• Received over $3 million as PI in external funding from
DoD Navair, ONR, NASA; over 80 publications in top-tier
conferences and journals
• Currently 8 members including
• 2 post-doctoral researchers with Ph.D. in robotics
(electrical, control, mechanical engineering) and vision
• 4 graduate students (computer science)
• 1 undergraduate students (computer engineering,
computer science)
• Collaborations with faculty from Mechanical engg,
Computer science (UN-Lincoln, U. Southern Mississippi),
Mathematics (UNO)
6/16/2014 Raj Dasgupta, CMANTIC Lab, UNO 4

5. AVAILABLE ROBOT PLATFORMS
E-puck mini robot -
suitable for table-top
experiments for proof-of-
Coroware Corobot (indoor
robot)
• Suitable for indoor experiments in; Coroware Explorer
6/16/2014 Raj Dasgupta, CMANTIC Lab, UNO 5
experiments for proof-of-
concept
• Suitable for indoor experiments in;
hardware and software compatible
with Coroware Explorer robot;
• Sensors: Laser, IR, fixed camera;
Stargazer (IR-based indoor
localization); Wifi
Coroware Explorer
(outdoor robot) – all terrain robot for
outdoor experiments; customized with GPS,
compass for localization
All techniques are first verified on Webots simulator using
simulated models of e-puck and Corobot robots
Turtlebot (indoor robot)
• Suitable for experiments in indoor
arena within lab;
• Kinect sensor; IR
Pelican UAV
(aerial robot)
• Newly acquired
robot
• Sensors: Camera;
gyro

6. RESEARCH PROBLEM
• How to coordinate a set of robots to perform a set
of complexcomplex tasks in a collaborativecollaborative manner
• Complex task: single robot does not have resources to
complete the task individually
• Coordination can be synchronous or asynchronous
Robots might or might not have to perform the task at the same• Robots might or might not have to perform the task at the same
time
• Performance metric(s) need to be optimized while
performing tasks
• Time to complete tasks, distance traveled, energy expended
• Robots are able to communicate with each other
• Bluetooth, Wi-fi, IR, Camera, Laser
• Some robots can fail, but system should not stall
6/16/2014 Raj Dasgupta, CMANTIC Lab, UNO
6

7. APPLICATIONS
• Humanitarian de-mining (COMRADES)
• Autonomous exploration for planetary surfaces
(ModRED)
• Automatic Target Recognition (ATR) for search and
recon (COMSTAR)recon (COMSTAR)
• Unmanned Search and Rescue
• Civlian and domestic applications like agriculture,
vaccum cleaning, etc.
6/16/2014 Raj Dasgupta, CMANTIC Lab, UNO
7

8. GAME THEORY WORKSHOP
DAY 1
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 8

9. OBJECTIVE
• Introduction to game theory from a computer
science perspective
• Learn the fundamental concepts in game theory
• Mathematical solution concepts
• Algorithms used to solve games• Algorithms used to solve games
• Applications of game theory in different application
domains
• Google Adwords
• Trading Agent Competition (Lemonade Stand Game)
• Develop programming tools for solving game theory
problems and preparation for advanced graduate
coursework
June 16-20, 2014 9Game Theory Workshop - Raj Dasgupta

10. OUTCOMES
• Write software for algorithms for
• Supply chain management – energy market, travel
booking, warehouse inventory management
• Auctions (e-bay, etc)
• Ad-placement (ad-auctions) for Internet search engines,• Ad-placement (ad-auctions) for Internet search engines,
Youtube, etc.
• Applications that require coordination between people or
software agents
• Social networks – information aggregation
• Robotics – distributed robot systems
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 10

11. ADX GAME
• An Ad Network
bids for display
ads
opportunities
• Fulfill advertising
contracts atcontracts at
minimum cost
• High quality
targeting
• Sustain and
attract
advertisers
• https://sites.google.c
om/site/gameadx/
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 11

12. POWER-TAC GAME
• Agents act as retail brokers in a local power
distribution region
• Purchasing power from wholesale market and local sources
• Sell power to local customers and into the wholesale
market.market.
• Solve a supply-chain problem
• Product is infinitely perishable
• Supply and demand must be exactly balanced at all times
• http://www.powertac.org
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 12

13. TOPICS TO BE COVERED
• Day 1: Introduction to game theory – normal form
games
• Day 2: Solution concepts for normal form games
(math)
Day 3: Bayesian games; applications of games• Day 3: Bayesian games; applications of games
• Day 4: Mechanism design and auctions
• Day 5: Coalition games and student presentations
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 13

14. STUDENT PRESENTATIONS
• Pick a topic on game theory that is covered in class
• Research on the Internet on your topic and find at least
one problem or challenge related to this problem
• Prepare a 10 minute presentation with slides (about 10-
12 slides)
• Give overview of topic• Give overview of topic
• Discuss the problem or challenge on the topic you have found
on the Internet
• Mention the most interesting or appealing concept that you
learned from the course and why it is interesting to you
• Presentation should reflect your understanding of the
topic
• Presentation schedule: reverse-alphabetical by last
name, Friday after lunch
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta 14

15. DAY 1: OUTLINE
• Introduction
• Some classic 2-player games
• Solving 2-players games
• Dominated strategies and iterated dominance
• Pareto optimality and Nash equilibrium• Pareto optimality and Nash equilibrium
• Mixed Strategies
• Software packages for solving games
• Generating games using GAMUT
• Solving games using Gambit
• Correlated Equilibrium
June 16-20, 2014 15Game Theory Workshop - Raj Dasgupta

16. HISTORY OF GAME THEORY
• 19th century and earlier: mathematical formulations to solve
taxation problems, profits, etc.
• First half of 20th century:
• Von Neumann formalizes utility theory, lays down mathematical
foundations for analyzing two player games; early work starts
• 1950s onwards: Nash theoremNash theorem, analysis of different types of
games, beyond two players, relaxing simplifying assumptionsgames, beyond two players, relaxing simplifying assumptions
(e.g., complete knowledge), more complex settings
• 1970s onwards: evolutionary game theory (applying biological
concepts in games), learning in games, mechanism design
• 1990s onwards:
• computational implementation of game theory algorithms, complexity
results (n players),
• game theory software, programming competitions,
• applications to real-life domains (auctions, network bandwidth
sharing, resource allocation, etc.)
June 16-20, 2014 16Game Theory Workshop - Raj Dasgupta

17. SOME NOTABLE GAME THEORISTS
• John Von Neumann – Founder of field
• John Nash – Nash equilibrium
• John Harsanyi – Incomplete Information
(Bayesian Games)(Bayesian Games)
• Roger Myerson – Mechanism Design
• Many others: Morgenstern, Selten, Maynard
Smith, Aumann…
June 16-20, 2014 17Game Theory Workshop - Raj Dasgupta

18. A SIMPLE EXAMPLE
• Simplest case: 2 players
• Each player has a set (2) of actions
• Each player has to select an action
• By doing action, the player gets a payoff or utility
• Rationality assumption: Each player selects action that gives it highest payoff
• A player’s decision (selected action) affects the other player’s decision
(selected action)
• And other player’s payoff, and in turn its own payoff• And other player’s payoff, and in turn its own payoff
Actions: Go, Stop
Payoff(Go) = 1
Payoff (Stop) = -1
Actions: Go, Stop
Payoff(Go) = 1
Payoff (Stop) = -1
June 16-20, 2014 18Game Theory Workshop - Raj Dasgupta

19. A SIMPLE EXAMPLE
• Simplest case: 2 players
• Each player has a set (2) of actions
• Each player has to select an action
• By doing action, the player gets a payoff or utility
• Rationality assumption: Each player selects action that gives it highest payoff
• A player’s decision (selected action) affects the other player’s decision
(selected action)
• And other player’s payoff, and in turn its own payoff• And other player’s payoff, and in turn its own payoff
Actions: Go, Stop
Actions: Go, Stop
Payoff(Go, Go) = -2, -2
Payoff (Go, Stop) = 2, -1
Payoff (Stop, Go) = -1, 2
Payoff (Stop, Stop) = -1, -1
Payoff(Go, Go) = -2, -2
Payoff (Go, Stop) = 2, -1
Payoff (Stop, Go) = -1, 2
Payoff (Stop, Stop) = -1,
-1
June 16-20, 2014 19Game Theory Workshop - Raj Dasgupta

20. A SIMPLE EXAMPLE
• Simplest case: 2 players
• Each player has a set (2) of actions
• Each player has to select an action
• By doing action, the player gets a payoff or utility
• Rationality assumption: Each player selects action that gives it highest payoff
• A player’s decision (selected action) affects the other player’s decision
(selected action)
• And other player’s payoff, and in turn its own payoff• And other player’s payoff, and in turn its own payoff
20
Actions: Go, Stop
Actions: Go, Stop
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
June 16-20, 2014 Game Theory Workshop - Raj Dasgupta

21. THE MAIN PROBLEM IN GAME
THEORY…SAID SIMPLY
• Main Problem: Given that each player knows the
actions and payoffs of each other, how can each
player individually make a decision (select an
action) that will be ‘best’ for itself
• ‘best’ is loosely defined
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
• ‘best’ is loosely defined
• Minimize regret
• Maximize sum of payoffs to all (both) players
• Stable or equilibrium action – if player deviates by itself from
that action, it will end up lowering its own payoff … should
hold for every player
Nash
Equilibrium
June 16-20, 2014 21Game Theory Workshop - Raj Dasgupta

22. MULTI-AGENT INTERACTIONS
• For solving game theory computationally,
players are implemented as software agents
• Main Problem (restated in terms of agents):
When two agents interact, what actionWhen two agents interact, what action
should each agent take?
• Simplifying (natural) assumption: agents are
self-interested
• each agent takes an action that maximizes its
own benefit
June 16-20, 2014 22Game Theory Workshop - Raj Dasgupta

23. PREFERENCES AND UTILITY
• Since two agents are acting, action is referred
to as joint action
• Each (joint) action results in a different outcome
• Selecting a joint action ≡ selecting an outcome
• Selecting the best (highest benefit) outcome is
modeled as a probability distribution over the
set of possible outcomes
• called the preferences of the agent over its set of
possible outcomes
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
Outcome
Joint actions: { (go, go) (go, stop), (stop, go) (stop, stop)}
June 16-20, 2014 23Game Theory Workshop - Raj Dasgupta

24. UTILITY FUNCTION
• Assign a numeric value to outcomes
• More preferred outcome, higher utility
• Called utility function
• Utility is also called payoff
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
• Utility is also called payoff
June 16-20, 2014 24Game Theory Workshop - Raj Dasgupta

25. NOTATIONS
• A: set of agents
• Ω = (ω1, ω2, ...): set of outcomes
• U: A X Ω R : utility function
→
→
June 16-20, 2014 25Game Theory Workshop - Raj Dasgupta

26. PREFERENCE RELATION
• Suppose i, j ε A and ω, ω’ ε Ω
• u( i, ω) >= u(i, ω’) means agent i prefers outcome ω over ω’
• also denoted as ui(ω) >= ui (ω’) or ω >=i ω‘
• Relation >= gives an ordering over Ω
• Satisfies following properties• Satisfies following properties
• reflexivity
• transitivity
• comparability
• substitubility
• decomposability
• >=: weak preference
• > : strong preference
• only satisfies transitivity and comparability
June 16-20, 2014 26Game Theory Workshop - Raj Dasgupta

27. AGENT INTERACTION MODEL
• Consider only 2 agents: i, j ε A
• i and j take their actions simultaneously
• Outcome ω ε Ω is a result of both i and j’s actions
(sometimes called joint outcome)
• Other assumptions• Other assumptions
• each agent has to take action
• each agent cannot see what action other agent has taken
(only knows outcome)
• We assume that each agent knows
• the set of possible actions of itself and the other agent
• the utility for each possible outcome both for itself and for
the other agent
• (that is, each agent knows entire game matrix)
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
June 16-20, 2014 27Game Theory Workshop - Raj Dasgupta

28. TRANSFORMATION FUNCTION
• τ: Ac X Ac Ω
• Ac: set of possible action
• τ : state transformation function
→
June 16-20, 2014 28Game Theory Workshop - Raj Dasgupta

29. EXAMPLE
• Let Ac = {C, D} for both agents
• Let τ(C,C) = ω1, τ(C,D) = ω2, τ(D,C) = ω3,
τ(D,D) = ω4
• Let ui(ω1)=4, ui(ω2)=4, ui(ω3)=1, ui(ω4)=1
• Let uj(ω1)=4, uj(ω2)=1, uj(ω3)=4, uj(ω4)=1
• Since each pair of joint actions gives one• Since each pair of joint actions gives one
specific joint outcome, we can write
• ui(C,c)=4, ui(C,d)=4, ui(D,c)=1, ui(D,d)=1
• uj(C,c)=4, uj(C,d)=1, uj(D,c)=4, uj(D,d)=1
• For agent i, the preference over outcomes
is
(C,c) >= i (C, d) > i (D,c) >=i (D,d)
June 16-20, 2014 29Game Theory Workshop - Raj Dasgupta

30. PAYOFF MATRIX
4, 4,C
dc
1, 1,
4,
D
Agent i
• Each entry gives (utility to agent i, utility to agent j)
June 16-20, 2014 30Game Theory Workshop - Raj Dasgupta

31. PAYOFF MATRIX
4,4 4,1C
dc
Agent j
1,4 1,1
4,1
D
Agent i
• Each entry gives (utility to agent i, utility to agent j)
June 16-20, 2014 31Game Theory Workshop - Raj Dasgupta

32. PAYOFF MATRIX
4,4 4,1C
dc
Agent j
1,4 1,1
4,1
D
Agent i
•For agent i, selecting C is always better than selecting D
irrespective of what agent j does
June 16-20, 2014 32Game Theory Workshop - Raj Dasgupta

33. PAYOFF MATRIX
4,4 4,1C
dc
Agent j
1,4 1,1
4,1
D
Agent i
•For agent j, selecting C is always better than selecting D
irrespective of what agent i does
June 16-20, 2014 33Game Theory Workshop - Raj Dasgupta

34. PAYOFF MATRIX
4,4 4,1C
dc
Agent j
1,4 1,1
4,1
D
Agent i
• Finally, (C, c) remains as the only feasible (rational) outcome
June 16-20, 2014 34Game Theory Workshop - Raj Dasgupta

35. DOMINANT STRATEGIES
• Let Ω={ω1, ω2, ω3, ω4}: be the set of possible
outcomes
• Let Ω1 and Ω2 be two proper subsets of Ω
such that Ω1={ω1, ω2} and Ω2={ω3, ω4}1 1 2 2 3 4
• Suppose that for some agent k, ω1 =k ω2 >k
ω3 =k ω4
• For agent k, every outcome in Ω1 is preferred
over every outcome in Ω2
• We say, for agent k, Ω1strongly dominates Ω2
June 16-20, 2014 35Game Theory Workshop - Raj Dasgupta

36. STRATEGIES
• Actions of agents are also called strategies
• Outcome of playing strategy s denoted by
s*
• For e.g.: (from previous example)• For e.g.: (from previous example)
• For agent i, C* = {ω3, ω4} and D* = {ω1, ω2}
• Using this notation, strategy s1 dominates
strategy s2 if every outcome in s1
* dominates
every outcome in s2
*
• For e.g, in previous example, C dominates D
for agent i (also for agent j)
June 16-20, 2014 36Game Theory Workshop - Raj Dasgupta

37. SOLVING A GAME WITH DOMINANT
STRATEGIES
• Solving a game means finding the outcome of
the game
• Procedure
1. Inspect strategies one at a time
2. If a strategy is strongly dominated by another strategy,2. If a strategy is strongly dominated by another strategy,
remove the dominated strategy
3. If the agent ends up with only one strategy by applying
step 2 repeatedly, then the remaining strategy is the
dominant strategy
June 16-20, 2014 37Game Theory Workshop - Raj Dasgupta

38. WEAKLY DOMINATED STRATEGY
• Let s1 and s2 be two strategies
• s1 weakly dominates s2 if every outcome in s1
* is >=
every outcome in s2
*
June 16-20, 2014 38Game Theory Workshop - Raj Dasgupta

39. NASH EQUILIBRIUM

40. PRISONER’S DILEMMA GAME
• Two men are together charged with the
same crime and held in separate cells. They
have no way of communicating with each
other, or, making an agreement
beforehand. They are told thatbeforehand. They are told that
• if one of them confesses the crime and the other
does not, the confessor will be freed while the
other person will get a term of 3 years
• if both confess the crime, each will get term of 2
years
• if neither confess the crime, each will get a 1-year
term
June 16-20, 2014 40Game Theory Workshop - Raj Dasgupta

41. PRISONER’S DILEMMA GAME
• Each person (player) has two strategies
• confess (C)
• don’t confess (D)
• Which strategy should each player play?
Remember each player is a self-interested utility• Remember each player is a self-interested utility
maximizer
June 16-20, 2014 41Game Theory Workshop - Raj Dasgupta

42. PD GAME: PAYOFF MATRIX
C D
C -2, -2 0, -3
Player 1
Player 2
Are there any strongly dominated strategies for any player?
C -2, -2 0, -3
D -3, 0 -1, -1
Player 1
June 16-20, 2014 42Game Theory Workshop - Raj Dasgupta

43. PD GAME REASONING
• Agent i reasons:
• I don’t know what j is going to play, but I know he will play
either C or D. Let me see what happens to me in either of
these cases.
• If I assume that J is playing C, I will get a payoff of –2 if if I
play C and a payoff of -3 if I plays Dplay C and a payoff of -3 if I plays D
• If I assume that J is playing D, I will get a payoff of 0 if if I play
C and a payoff of -1 if I plays D
• Therefore, irrespective of what J plays, I’m better off by
playing C
• Agent j reasons in a similar manner (since the game
is symmetric)
• Both end up playing (C, C)
C D
C -2, -2 0, -3
D -3, 0 -1, -1
June 16-20, 2014 43Game Theory Workshop - Raj Dasgupta

44. EXAMPLE: PRISONER’S DILEMMA
CD
D -2,-2 -10,-1
P2
• Utility values are changed from last example, order or
rows are interchanged
• Outcome of the game still remains same (C, C)
• Representation of the game does not change its
outcome as long as relative utility values remain same
C -1,-10 -5,-5
P1
June 16-20, 2014 44Game Theory Workshop - Raj Dasgupta

45. NASH EQUILIBRIUM
• Two strategies s1 and s2 are in Nash equilibrium
when
• under assumption agent i plays s1, agent j can do no better
than play s2
• under assumption agent j plays s2, agent i can do no better• under assumption agent j plays s2, agent i can do no better
than play s1
• Neither agent has any incentive to deviate from a
Nash equilibrium
June 16-20, 2014 45Game Theory Workshop - Raj Dasgupta

46. PD GAME EQUILIBRIUM
• Is (C, C) a Nash equilibrium of the game?
• given agent j is playing C, agent i can do no
better than play C
• given agent i is playing C, agent j can do no
better than play Cbetter than play C
• Is (D, D) a Nash equilibrium of the game?
• given agent j is playing D, agent i can do better
by playing C
• given agent i is playing D, agent j can do better
by playing C
C D
C -2, -2 0, -3
D -3, 0 -1, -1
June 16-20, 2014 46Game Theory Workshop - Raj Dasgupta

47. EXAMPLE: NASH EQUILIBRIUM
June 16-20, 2014 47Game Theory Workshop - Raj Dasgupta

48. FEATURES OF NASH EQUILIBRIUM
• Not every game has a Nash equilibrium in pure
strategies
• Nash’s Theorem
• Every game with a finite number of players and action
profiles has at least one Nash equilibrium (considering pureprofiles has at least one Nash equilibrium (considering pure
and mixed strategies)
• Some interaction scenarios have more than one
Nash equilibrium
June 16-20, 2014 48Game Theory Workshop - Raj Dasgupta

49. GAMES WITH MULTIPLE NASH
EQUILIBRIUM
• Game of chicken (Earlier bridge crossing example)
• Stag-hunt
Go Stop
Go -2, -2 2, -1
Stop -1, 2 -1, -1
Stag Hare
Stag 2, 2 0,1
Hare 1, 0 1, 1
June 16-20, 2014 49Game Theory Workshop - Raj Dasgupta

50. COMPETITIVE AND ZERO-SUM GAMES
• Strictly competitive game
• For i, j ε A, ω, ω’ ε Ω : ω >i ω’ iff ω’ >j ω
• preferences of the players are diametrically opposite to
each other
• Zero-sum game• Zero-sum game
• for all ω ε Ω: ui(ω) + uj(ω) = 0
• zero sum games have no chance of cooperative behavior
because positive utility for agent j means negative utility for
agent i and vice-versa
June 16-20, 2014 50Game Theory Workshop - Raj Dasgupta

51. ZERO-SUM GAME: MATCHING
PENNIES
• Two players simultaneously flip two pennies. If
both have the same side up, player 1 keeps
both of them, else player 2.
Agent j
1, -1
-1, 1 1, -1
-1,1H
T
TH
Agent i
Agent j
June 16-20, 2014 51Game Theory Workshop - Raj Dasgupta

52. ITERATED DOMINANCE:
DISTRICT ATTORNEY’S BROTHER
• Recall: Given a game, to solve it, first remove all
strictly dominated strategies
• All games might not have strictly dominated
strategies
• Try iterated removal of dominated strategies• Try iterated removal of dominated strategies
• Same scenario as prisoners’ dilemma except:
• one of the prisoners is the DA’s brother
• allows his brother (prisoner 1) to go free if both prisoners
don’t confess
June 16-20, 2014 52Game Theory Workshop - Raj Dasgupta

53. EXAMPLE: PRISONER’S DILEMMA
Prisoners’ Dilemma DA’s Brother
C D
C -2, -2 0, -3
D -3, 0 -1, -1
C D
C -2, -2 0, -3
D -3, 0 0, -1
• For players 1 and 2, D is strictly
dominated
• Therefore, (C, C) is the preferred
strategy (and Nash outcome)
• For player 1 D is not strictly
dominated now
• But, for player 2, D is still strictly
dominated
• Player 1 reasons – Player 2 will
never play D
• Now, D becomes strictly
dominated for player 1
• (C, C) still remains outcome of
game
Strict dominance: Each player can
solve the game individually
Iterated dominance: A player has to
build opponent’s model to solve the
gameJune 16-20, 2014 53Game Theory Workshop - Raj Dasgupta

54. ASSUMPTIONS IN DA’S BROTHER
• Each player is rational
• Players have common knowledge of each other’s
rationality
• P1 knows P2 will behave in a rational manner
• Allows iterated deletion of dominated strategies• Allows iterated deletion of dominated strategies
• However: Each iteration requires common
knowledge assumption to be one level deeper
June 16-20, 2014 54Game Theory Workshop - Raj Dasgupta

55. ITERATED STRATEGY DELETION:
ORDER OF DELETION
• Order of deletion does not have effect on final
outcome of game
• if eliminated strategies are strongly dominated
• Order of deletion has effect on final outcome of
gamegame
• if eliminated strategies are weakly dominated
June 16-20, 2014 55Game Theory Workshop - Raj Dasgupta

56. COMMON PAYOFF GAME
• Both (all) agents get equal utility in every
outcome (e.g., two drivers coming from opposite
sides have to choose which side of road to drive
on)
1, 1
0, 0 1, 1
0, 0L
R
RL
Agent i
Agent j
June 16-20, 2014 56Game Theory Workshop - Raj Dasgupta

57. BATTLE OF SEXES GAME
• Husband prefers going to a football
game, which wife hates
• Wife prefers going to the opera, which
husband hateshusband hates
• They like each other’s company
2, 1
0, 0 1, 2
0, 0F
O
OF
h
w
June 16-20, 2014 57Game Theory Workshop - Raj Dasgupta

58. DEFINITION: NORMAL FORM GAME
• For a game with I players, the normal form
representation of the game ΓN specifies for
each player i, a set of strategies Si (with si Є Si)
and a payoff or utility function ui(s1, s2, s3,
s …s) giving the utility associated with thes4…sI) giving the utility associated with the
outcome of the game corresponding to the
joint strategy profile (s1, s2, s3, s4…sI).
• Formal notation:
ΓN =[ I, {Si}, {ui(.)}]
June 16-20, 2014 58Game Theory Workshop - Raj Dasgupta

59. DEFINITION:
STRICTLY DOMINATED STRATEGY
• A strategy si Є Si is strictly dominated for player I in
game ΓN =[ I, {Si}, {ui(.)}] if there exists another
strategy si
‘ Є Si such that for all s-i Є S-i
ui(si
‘,s-i) > ui(si,s-i)ui(si
‘,s-i) > ui(si,s-i)
• In this case we say that strategy si
‘ strictly
dominates strategy si
June 16-20, 2014 59Game Theory Workshop - Raj Dasgupta

60. EXAMPLE: STRICT DOMINANCE
RL
U 1, -1 -1, 1
P1
P2
D
M -1, 1 1, -1
-2, 5 -3, 2
P1
• For player 1, D is strictly dominated by U and M
June 16-20, 2014 60Game Theory Workshop - Raj Dasgupta

61. DEFINITION:
WEAKLY DOMINATED STRATEGY
• A strategy si Є Si is weakly dominated for player I in
game ΓN =[ I, {Si}, {ui(.)}] if there exists another
strategy si
‘ Є Si such that for all s-i Є S-i
ui(si
‘,s-i) >= ui(si,s-i)i i -i i i -i
• with strict inequality for some s-i. In this case,
we say that strategy si
‘ weakly dominates
strategy si
• A strategy is a weakly dominant strategy for
player I in game ΓN =[ I, {Si}, {ui(.)}] if it weakly
dominates every other strategy in Si
June 16-20, 2014 61Game Theory Workshop - Raj Dasgupta

62. EXAMPLE: WEAK DOMINANCE
RL
U 5,1 4,0
P1
P2
D
M 6,0 3,1
6,4 4,4
P1
• For player 1, U and M are weakly dominated by D
June 16-20, 2014 62Game Theory Workshop - Raj Dasgupta

63. MIXED STRATEGIES

64. ZERO-SUM GAME: MATCHING
PENNIES
• Is there a Nash equilibrium in pure strategies?
TH
Agent j
1, -1
-1, 1 1, -1
-1,1H
T
Agent i
June 16-20, 2014 64Game Theory Workshop - Raj Dasgupta

65. MIXED STRATEGY NASH EQUILIBRIUM
• Objective
• Each player randomizes over its own strategies in a way
such that its opponents’ choice becomes independent of it
actions
June 16-20, 2014 65Game Theory Workshop - Raj Dasgupta

66. SOLVING MIXED STRATEGY NASH
EQUILIBRIUM (1)
• P1 tries to solve: What probability should I play H and T
with so that my (expected) utility is independent of
H T
H 1, -1 -1, 1
T -1, 1 1, -1
P1
P2
p
1-p
• P1 tries to solve: What probability should I play H and T
with so that my (expected) utility is independent of
whether P2 plays H or T
• Suppose P1 plays H with probability ‘p’ and T with
probability (1-p)
• Utility to PI when P2 plays H: 1.p + (-1) (1-p) = 2p -1
• Utility to PI when P2 plays T: (-1)1.p + 1.(1-p) = 1 – 2p
• To find mixed strategy P1 solves for p in:
• 2p -1 = 1- 2p, or, p = 0.5
June 16-20, 2014 66Game Theory Workshop - Raj Dasgupta

67. SOLVING MIXED STRATEGY NASH
EQUILIBRIUM (2)
H T
H 1, -1 -1, 1
T -1, 1 1, -1
P1
P2
1-qq
0.5
0.5
0.5 0.5
• P2 solves similarly denotes q as probability of
playing H and (1-q) as probability for playing T
• Solving for q in the same manner as for P1 gives q = 0.5
• Mixed strategy Nash equilibrium is:
• ((0.5, 0.5) (0.5, 0.5))
June 16-20, 2014 67Game Theory Workshop - Raj Dasgupta

68. EXAMPLE: MEETING IN NY GAME:
MIXED STRATEGY NASH
EQUILIBRIUM
June 16-20, 2014 68Game Theory Workshop - Raj Dasgupta

69. EXAMPLE: MEETING IN NY GAME:
MIXED STRATEGY NASH
EQUILIBRIUM (2)
• T reasons:
• Let me play GC with probability σs and ES with probability (1- σs)
• Then,
• if S plays G it gets a payoff 100 σs + 0(1- σs)
• if S plays E it gets a payoff 0 σs +1000(1- σs)
• Recall:
• Each player should play its strategies with such probabilities that it• Each player should play its strategies with such probabilities that it
does not matter to its opponent what strategy that player plays.
• In other words, T should be indifferent (get the same payoff)
from either strategy that S plays
• Therefore,
• 100 σs + 0(1- σs) = 0 σs +1000(1- σs)
• or, 1100σs =1000, or, σs = 10/11
• By similar reasoning, S plays GC with probability σT =10/11
• σs = σT = 10/11 constitutes a mixed strategy nash equilibrium of
the meeting in NY game
June 16-20, 2014 69Game Theory Workshop - Raj Dasgupta

70. BATTLE OF SEXES GAME
• Husband prefers going to a football
game, which wife hates
• Wife prefers going to the opera, which
husband hateshusband hates
• They like each other’s company
2, 1
0, 0 1, 2
0, 0F
O
OF
h
w
June 16-20, 2014 70Game Theory Workshop - Raj Dasgupta

71. DEFINITION: MIXED STRATEGY
• Given player i’s (finite) pure strategy set Si, a
mixed strategy for player i , σi: Si → [0,1],
assigns to each pure strategy si Є Si a
probability σi(si) >=0 that it will be played,
where Σ si Є Si σi(si) =1where Σ si Є Si σi(si) =1
• The set of all mixed strategies for player i is
denoted by ∆(Sj)={(σ1,σ2,σ3,... ,σMi) Є RM: σmi >0
for all m = 1...M and Σm=1
Μ σmi=1
• ∆(Sj) is called the mixed strategy profile
• si is called the support of the mixed strategy
σi(si)
June 16-20, 2014 71Game Theory Workshop - Raj Dasgupta

72. DEFINITION: STRICT DOMINATION
IN MIXED STRATEGIES
• A strategy σi Є ∆(Si) is strictly dominated for player i
in game ΓN =[ I, {∆(Si)}, {ui(.)}] if there exists
another strategy σi
‘ Є ∆(Si) such that for all σ-i Є Π
j<>i ∆(Sj)
ui(σi
‘, σ-i) > ui(σi, σ-i)ui(σi
‘, σ-i) > ui(σi, σ-i)
• In this case we say that strategy σi
‘ strictly
dominates strategy σi
• A strategy σi is a strictly dominant strategy
for player i in game ΓN =[ I, {∆(Si)}, {ui(.)}] if it
strictly dominates every other strategy in
∆(Sj)
June 16-20, 2014 72Game Theory Workshop - Raj Dasgupta

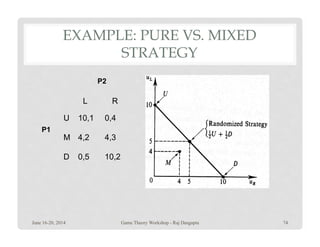
73. PURE VS. MIXED STRATEGY
• Player i’s pure strategy is strictly dominated in game
ΓN =[ I, {∆(Si)}, {ui(.)}] if and only if there exists
another strategy σi
‘ Є ∆(Si) such that
ui(σi
‘, s-i) > ui(si, s-i)ui(σi , s-i) > ui(si, s-i)
for all s-i Є S-i
June 16-20, 2014 73Game Theory Workshop - Raj Dasgupta

74. EXAMPLE: PURE VS. MIXED
STRATEGY
RL
U 10,1 0,4
P2
D
M 4,2 4,3
0,5 10,2
P1
June 16-20, 2014 74Game Theory Workshop - Raj Dasgupta

75. BEST RESPONSE AND
NASH EQUILIBRIUM
• In a game ΓN =[ I, {∆(Si)}, {ui(.)}] , strategy s*
i is
a best response for player i to its opponents’
strategies s-i if
ui(s*
i, s-i) >= ui(si, s-i)ui(s*
i, s-i) >= ui(si, s-i)
for all si ε ∆(Si).
• A strategy profile s = (s*
1 ,s*
2 … s*
N) is a Nash
equilibrium if s*
i is a best response for all
players i= 1…N
June 16-20, 2014 75Game Theory Workshop - Raj Dasgupta

76. DELETION OF NEVER A BEST
REPONSE
• Strategy si is never a best response if there is no s-i for
which si is a best response
• Strictly dominated strategy can never be a best
response
• Converse is not true: A strategy that is not a strictly• Converse is not true: A strategy that is not a strictly
dominated might be ‘never a best response’
• Therefore, eliminating strategies that are ‘never a
best response’ eliminates
• strictly dominated strategies
• possibly some more strategies
June 16-20, 2014 76Game Theory Workshop - Raj Dasgupta

77. ITERATED DELETION
• Never a best response strategies can be
removed in an iterated manner using
rational behavior and common knowledge
(similar to iterated deletion of strictly
dominated strategies)dominated strategies)
• Order of deletion does not affect the
strategies that remain in the end
• Strategies that remain after iterated deletion
are those that a player can rationalize
assuming opponents also eliminate their
never a best reponse strategies
June 16-20, 2014 77Game Theory Workshop - Raj Dasgupta

78. RATIONALIZABLE STRATEGIES
• In game ΓN =[ I, {∆(Si)}, {ui(.)}], the strategies in ∆(Si)
that survive the iterated removal of strategies that
are never a best response are known as player i’s
rationalizable strategies.
June 16-20, 2014 78Game Theory Workshop - Raj Dasgupta

79. WHY WILL A GAME HAVE
A NASH EQUILIBRIUM
1. Nash equilibrium as a consequence of
rational inference
2. Nash equilibrium as a necessary condition
if there is a unique predicted outcome to
the gamethe game
3. Focal Points
• e.g: restaurants around Grand Central Station
are better than those around Empire State
Building. Increases the payoff of meeting at
Grand Central
4. Nash equilibrium as a self-enforcing
agreement
5. Nash equilibrium as a stable social
conventionJune 16-20, 2014 79Game Theory Workshop - Raj Dasgupta

80. MAXMIN STRATEGY
• Maxmin strategy maximizes the worst payoff that
player i can get
s i
maxmin = arg max s_i min s_-i ui(si, s-i)
• Find the set of my strategies that give me the
minimum utilities corresponding to every jointminimum utilities corresponding to every joint
strategy of the opponent players (everybody
except me)
• Find the strategy that gives me the highest utility
from the set in the previous step
June 16-20, 2014 80Game Theory Workshop - Raj Dasgupta

81. MINMAX STRATEGY FOR 2-PLAYER
GAME
• Minmax strategy – player i minimizes the
highest payoff that player –i (opponent) can
get
s i
minmax = arg min s_i max s_-i u-i(si, s-i)s i = arg min s_i max s_-i u-i(si, s-i)
• Find the set of my strategies that give my
opponent the maximum utilities
corresponding to each of my strategies
• Find my strategy from the set in the previous
step that gives the lowest utility to my
opponent
June 16-20, 2014 81Game Theory Workshop - Raj Dasgupta

82. MINMAX UTILITY FOR N-PLAYER GAME
• i will have one minmax strategy for each opponent
• In an n-player game, the minmax strategy for player
i against player j (not equal to i) is i’s component of
the mixed strategy profile s-j in the expression arg
min max u(s, s ), where –j denotes the set ofmin s_-j max s_j uj(sj, s-j), where –j denotes the set of
players other than j
June 16-20, 2014 82Game Theory Workshop - Raj Dasgupta

83. NASH EQUILIBRIUM VS.
MINMAX/MAXMIN STRATEGY
• In any finite, two-player, zero-sum gane, in any Nash
equilibrium, each player receives a payoff that is
euqal to both his maxmin value and his minmax
value
June 16-20, 2014 83Game Theory Workshop - Raj Dasgupta

84. REGRET
• An agent i’s regret for playing an strategy si if the
other agent’s joint strategy profile is s-i is defined as
[max s’_i ε S_i ui(si’, s-i)] - ui(si, s-i)
• An agent i’s max regret is defined as
max s_-i’ ε S_-i [max s’_i ε S_i ui(si’, s-i)] - ui(si, s-i)
• An agent i’s minimax regret is defined as
arg min s_i ε S_i (max s_-i’ ε S_-i [max s’_i ε S_i ui(si’, s-i)] - ui(si, s-
i))
June 16-20, 2014 84Game Theory Workshop - Raj Dasgupta