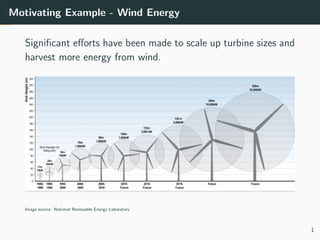
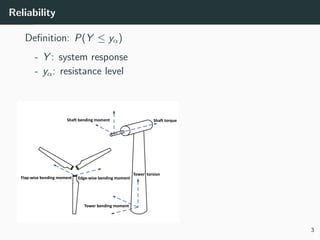
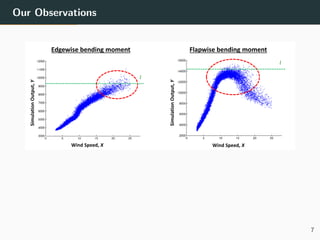
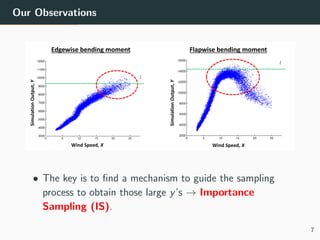
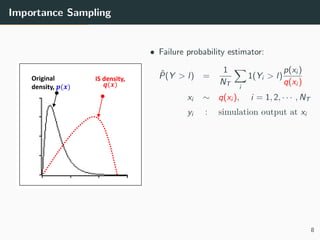
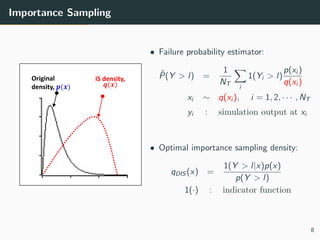
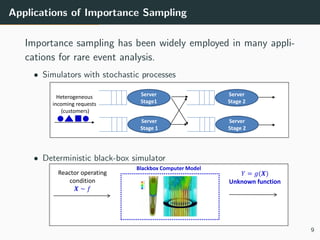
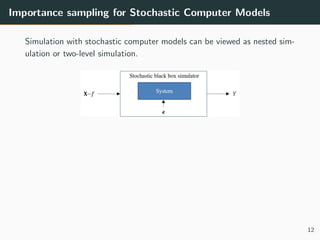
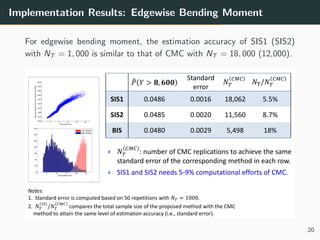
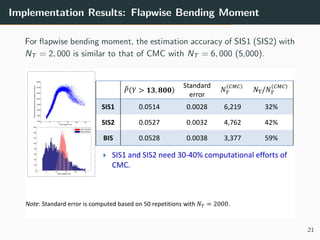
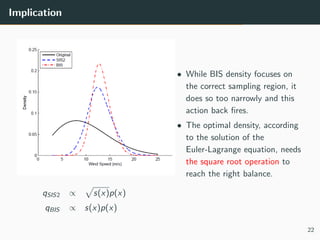
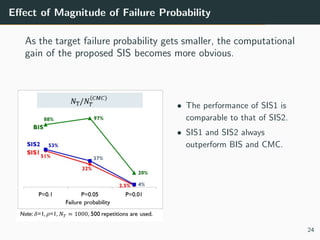
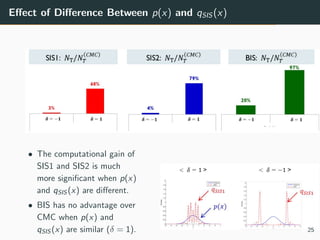
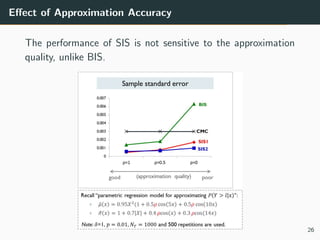
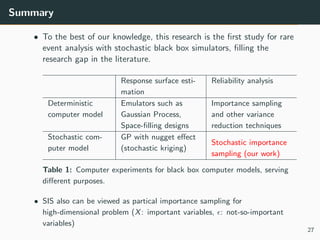
This document discusses the use of variance reduction techniques, specifically importance sampling, for reliability assessment in wind turbine design utilizing stochastic computer models. The research highlights the limitations of conventional Monte Carlo simulations and introduces a novel approach that optimally allocates computational resources to estimate failure probabilities more accurately and efficiently. Future plans include exploring new modeling techniques and extending the approach to address multiple outputs and high-dimensional inputs.

1. Variance Reduction for Reliability Assessment
with Stochastic Computer Models
Eunshin Byon, PhD
Associate professor
Industrial & Operations Engineering
Civil & Environmental Engineering
University of Michigan

2. Motivating Example - Wind Energy
Significant efforts have been made to scale up turbine sizes and
harvest more energy from wind.
Image source: National Renewable Energy Laboratory
1

3. Motivating Example - Wind Energy
Increasing size and mass of a wind turbine add the structural
and mechanical loads imposed on a turbine.
⇒ It is crucial to design a turbine with a high reliability level,
so it can operate over its intended design period (20-50 years).
2

4. Reliability
Definition: P(Y ≤ yα)
- Y : system response
- yα: resistance level
Edge-wise bending momentFlap-wise bending moment
Tower bending moment
Tower torsion
Shaft bending moment Shaft torque
3

5. Reliability
Definition: P(Y ≤ yα)
- Y : system response
- yα: resistance level
Edge-wise bending momentFlap-wise bending moment
Tower bending moment
Tower torsion
Shaft bending moment Shaft torque
• Two types of reliability:
- Reliability under
extreme shock, e.g.,
“extreme load”
- Reliability under
progressive damage,
e.g., “fatigue load”
3

6. Failure Probability
Failure probability under stochastic operating conditions:
P(Y > yα) = P(Y > yα|x)p(x)dx
• p(x): pre-specified pdf of input operating condition X
(site-specific density of wind speed or density specified in
design standard)
4

7. NREL’s Aeroelastic Simulator
Due to data scarcity at the design stage, designers often use sim-
ulations, e.g, National Renewable Energy Laboratory (NREL)’s
aeroelastic simulators.
Wind condition
(e.g., 10-minute
average wind speed,
turbulence level)
TurbSim generates
3D wind profile
FAST/AeroDyn generates load responses
at turbine components
5

8. If We Use Crude Monte Carlo (CMC) simulation
6

9. If We Use Crude Monte Carlo (CMC) simulation
• Computationally expensive
• Manuel (2013) uses a Linux
computer cluster at Sandia
National laboratories with
1,024 cores.
• When failure probability is on
the order of 10−7
, more than
107
simulations require 23 ∼
28 days of running to observe
one extreme event on a
regular desktop.
• Large variance (uncertainty)
in estimations
6

10. Our Observations
Edgewise bending moment
Wind Speed, X
Flapwise bending moment
Wind Speed, X
SimulationOutput,Y
SimulationOutput,Y
𝑙
𝑙
7

11. Our Observations
Edgewise bending moment
Wind Speed, X
Flapwise bending moment
Wind Speed, X
SimulationOutput,Y
SimulationOutput,Y
𝑙
𝑙
• The key is to find a mechanism to guide the sampling
process to obtain those large y’s → Importance
Sampling (IS).
7

12. Importance Sampling
Original
density, 𝒑(𝒙)
IS density,
𝒒(𝒙)
• Failure probability estimator:
ˆP(Y > l) =
1
NT
i
1(Yi > l)
p(xi )
q(xi )
xi ∼ q(xi ), i = 1, 2, · · · , NT
yi : simulation output at xi
8

13. Importance Sampling
Original
density, 𝒑(𝒙)
IS density,
𝒒(𝒙)
• Failure probability estimator:
ˆP(Y > l) =
1
NT
i
1(Yi > l)
p(xi )
q(xi )
xi ∼ q(xi ), i = 1, 2, · · · , NT
yi : simulation output at xi
• Optimal importance sampling density:
qDIS (x) =
1(Y > l|x)p(x)
p(Y > l)
1(·) : indicator function
8

14. Applications of Importance Sampling
Importance sampling has been widely employed in many appli-
cations for rare event analysis.
• Simulators with stochastic processes
Heterogeneous
incoming requests
(customers)
Server
Stage1
Server
Stage 1
Server
Stage 2
Server
Stage 2
• Deterministic black-box simulator
𝑌 = 𝑔(𝑿)
Unknown function
Blackbox Computer Model
Reactor operating
condition
𝑿 ∼ 𝑓
9

15. Limitations of Existing Importance Sampling
• Existing importance sampling considers simulators where
the output is deterministic given an input condition.
Recall:
qDIS (x) =
1(Y > l|x)p(x)
p(Y > l)
• The joint density p(x) of all random variables used in
simulation should be known.
• However, NREL simulator does not satisfy this condition!
10

16. What is Unique in NREL Simulator?
The NREL simulator uses a stochastic black-box computer model.
Wind speed, x,
with known density, 𝑝 𝑥
𝑌 = 𝑔 𝑿, 𝝐 ,
𝑿 ~ 𝑝
𝝐 ~ 𝑢𝑛𝑘𝑛𝑜𝑤𝑛
Over 8 million random inputs, 𝝐,
with unknown joint density
(controllable)
(uncontrollable)
Stochastic Computer Model
Stochastic load
responses
11

17. What is Unique in NREL Simulator?
The NREL simulator uses a stochastic black-box computer model.
Wind speed, x,
with known density, 𝑝 𝑥
𝑌 = 𝑔 𝑿, 𝝐 ,
𝑿 ~ 𝑝
𝝐 ~ 𝑢𝑛𝑘𝑛𝑜𝑤𝑛
Over 8 million random inputs, 𝝐,
with unknown joint density
(controllable)
(uncontrollable)
Stochastic Computer Model
Stochastic load
responses
• is used to represent the stochastic turbulence around rotor blades.
• The relationship between X and is governed by physical rules and
constraints → their joint density does not take an explicit form.
• High dimensional random input inside the simulators.
11

18. Importance sampling for Stochastic Computer Models
Simulation with stochastic computer models can be viewed as nested sim-
ulation or two-level simulation.
12

19. Importance sampling for Stochastic Computer Models
Simulation with stochastic computer models can be viewed as nested sim-
ulation or two-level simulation.
• Under the existing IS scheme, qDIS (x, ) = 1(Y >l|x, )p(x, )
p(Y >l) , but
p(x, ) is unknown.
• In fact, from p(x, ) = p(x)p( |x), we only know p(x).
• Thus, we can apply IS to X only, but cannot apply to .
q(x, ) = q(x)q( |x) = q(x)f ( |x)
12

20. Sampling Procedure
Original
density, 𝒑(𝒙)
Stochastic
importance
sampling
distribution
𝒒 𝑿(𝒙)
𝒙 𝟏, ⋯ , 𝒙 𝑴
⋮
𝐢𝐧𝐩𝐮𝐭 𝐟𝐚𝐜𝐭𝐨𝐫
Sampled weather
conditions from 𝒒 𝑿(𝒙) Estimate the
failure
probability
with bias
correction
Focusing sampling efforts on
important weather conditions
Capturing stochastic outputs
due to 𝝐
Unbiased
evaluation
Run simulator 𝑵𝑖 times
and evaluate the
conditional density at
each 𝒙𝒊
• Failure probability estimator
ˆP(Y > l) =
1
M
M
i=1

 1
Ni
Ni
j=1
1(yij > l|xi )

 p(xi )
q(xi )
xi ∼ q(x), i = 1, 2, · · · , M, yij : jth
simulation output at xi
• What is optimal qX (x) and Ni ’s that can minimize the variance?
13

21. Derivation of Optimal Importance Sampling
From principles of the calculus of variations, given the total computational
resource NT , we obtain the optimal IS density and allocation that minimize
the estimator variance.
14

22. Optimal Importance Sampling
qSIS1(x) =
1
cq1
1
NT
s(x)(1 − s(x)) + s(x)2
Ni = NT
NT (1−s(xi ))
1+(NT −1s (xi ))
j
NT (1−s(xj ))
1+(NT −1s (xj ))
, i = 1, 2, · · · , M
where s(x) = P(Y > l|x).
• We call this method Stochastic Importance Sampling 1 (SIS1)
15

23. Optimal Importance Sampling
qSIS1(x) =
1
cq1
1
NT
s(x)(1 − s(x)) + s(x)2
Ni = NT
NT (1−s(xi ))
1+(NT −1s (xi ))
j
NT (1−s(xj ))
1+(NT −1s (xj ))
, i = 1, 2, · · · , M
where s(x) = P(Y > l|x).
• We call this method Stochastic Importance Sampling 1 (SIS1)
• When we limit Ni =1, the optimal IS density (called SIS2) takes the
following form:
qSIS2(x) =
1
cq2
s(x)p(x)
15

24. Benchmark Importance Sampling
One might argue that the following IS density, qBIS (x), mimics
the conventional IS density, qDIS (x).
16

25. Application to NREL Simulation Setting
• Input (X): wind speed, following the IEC standard, IEC 61400-1.
• Input density p(x) = fR (x)
FR (xout )−FR (xin)
• FR (x) = 1 − e
− x2
2τ2 : cumulative distribution function of Rayleigh
distribution with a scale parameter, τ = 1/π · 10
• fR (x): Rayleigh density function
• Output (Y ): 10-minute maximum response of flapwise and edgewise
bending moment
17

26. Approximation of Conditional Failure Probability
SIS1, SIS2 and BIS require the conditional failure probability, s(x) =
P(Y > l|x). Recall
qSIS1(x) ∝
1
NT
s(x)(1 − s(x)) + s(x)2p(x)
qSIS2(x) ∝ s(x)p(x)
qBIS ∝ s(x)p(x)
18

27. Approximation of Conditional Failure Probability
SIS1, SIS2 and BIS require the conditional failure probability, s(x) =
P(Y > l|x). Recall
qSIS1(x) ∝
1
NT
s(x)(1 − s(x)) + s(x)2p(x)
qSIS2(x) ∝ s(x)p(x)
qBIS ∝ s(x)p(x)
We take a small-size pilot sample and approximate s(x) using a non-
homogeneous Generalized Extreme Value (GEV) distribution.
˜P(Y > l|x) = 1 − exp − 1 +
y − µ(x)
σ(x)
ξ
ξ
18

28. Approximation of Conditional Failure Probability
• In the non-homogeneous GEV, we model µ(x) and σ(x) using cubic
spline functions.
• To estimate spline parameters, we maximize the log-likelihood
function penalized by the roughness of µ(x) and σ(x), based on
Generalized additive models for location, scale and shape (GAMLSS)
proposed by Rigby and Stasinopoulos (2005).
< Estimated location parameter > < Estimated scale parameter >
19

29. Implementation Results: Edgewise Bending Moment
For edgewise bending moment, the estimation accuracy of SIS1 (SIS2)
with NT = 1, 000 is similar to that of CMC with NT = 18, 000 (12,000).
𝑃 𝑌 > 𝟖, 𝟔𝟎𝟎
Standard
error
𝑁 𝑇
𝐶𝑀𝐶
𝑁T/𝑁 𝑇
𝐶𝑀𝐶
SIS1 0.0486 0.0016 18,062 5.5%
SIS2 0.0485 0.0020 11,560 8.7%
BIS 0.0480 0.0029 5,498 18%
Notes:
1. Standard error is computed based on 50 repetitions with 𝑁 𝑇 = 1000.
2. 𝑁 𝑇
𝐼𝑆
/𝑁 𝑇
𝐶𝑀𝐶
compares the total sample size of the proposed method with the CMC
method to attain the same level of estimation accuracy (i.e., standard error).
 𝑁 𝑇
𝐶𝑀𝐶
: number of CMC replications to achieve the same
standard error of the corresponding method in each row.
 SIS1 and SIS2 needs 5-9% computational efforts of CMC.
20

30. Implementation Results: Flapwise Bending Moment
For flapwise bending moment, the estimation accuracy of SIS1 (SIS2) with
NT = 2, 000 is similar to that of CMC with NT = 6, 000 (5,000).
 SIS1 and SIS2 need 30-40% computational efforts of
CMC.
Note: Standard error is computed based on 50 repetitions with 𝑁 𝑇 = 2000.
𝑃 𝑌 > 𝟏𝟑, 𝟖𝟎𝟎
Standard
error
𝑁 𝑇
𝐶𝑀𝐶
𝑁T/𝑁 𝑇
𝐶𝑀𝐶
SIS1 0.0514 0.0028 6,219 32%
SIS2 0.0527 0.0032 4,762 42%
BIS 0.0528 0.0038 3,377 59%
21

31. Implication
qSIS2 ∝ s(x)p(x)
qBIS ∝ s(x)p(x)
• While BIS density focuses on
the correct sampling region, it
does so too narrowly and this
action back fires.
• The optimal density, according
to the solution of the
Euler-Lagrange equation, needs
the square root operation to
reach the right balance.
22

32. Numerical Example
• Data generating structure:
X ∼ N(0, 1), Y |X ∼ N(µ(X), σ2
(X))
µ(X) = 0.95δX2
(1 + 0.5 cos(10X) + 0.5 cos(20X)),
σ(X) = 1 + 0.7|X| + 0.4 cos(X) + 0.3 cos(14X).
• Conditional probability is approximated with
ˆµ(X) = 0.95δX2
(1 + 0.5ρ cos(10X) + 0.5ρ cos(20X)),
ˆσ(X) = 1 + 0.7|X| + 0.4ρ cos(X) + 0.3ρ cos(14X).
We investigate the effects of various factors:
(a) magnitude of target failure probability (0.01, 0.05, 0.1)
(b) difference between IS density and original density (δ = −1, 1)
(c) conditional probability approximation accuracy (ρ=0, 0.5, 1)
23

33. Effect of Magnitude of Failure Probability
As the target failure probability gets smaller, the computational
gain of the proposed SIS becomes more obvious.
• The performance of SIS1 is
comparable to that of SIS2.
• SIS1 and SIS2 always
outperform BIS and CMC.
24

34. Effect of Difference Between p(x) and qSIS (x)
• The computational gain of
SIS1 and SIS2 is much
more significant when p(x)
and qSIS (x) are different.
• BIS has no advantage over
CMC when p(x) and
qSIS (x) are similar (δ = 1). 25

35. Effect of Approximation Accuracy
The performance of SIS is not sensitive to the approximation
quality, unlike BIS.
26

36. Summary
• To the best of our knowledge, this research is the first study for rare
event analysis with stochastic black box simulators, filling the
research gap in the literature.
Response surface esti-
mation
Reliability analysis
Deterministic
computer model
Emulators such as
Gaussian Process,
Space-filling designs
Importance sampling
and other variance
reduction techniques
Stochastic com-
puter model
GP with nugget effect
(stochastic kriging)
Stochastic importance
sampling (our work)
Table 1: Computer experiments for black box computer models, serving
different purposes.
• SIS also can be viewed as partical importance sampling for
high-dimensional problem (X: important variables, : not-so-important
variables)
27

37. Future plans
• Explore other methods to model the importance sampler,
e.g. non-parametric methods and mixture density
methods.
• Extend the approach to the multiple outputs and/or
high-dimensional input vector.
• Incorporate with other variance reduction techniques (e.g.,
stratified sampling, control variates)
28

38. Thank You!
For more information:
Dr. Eunshin Byon
Department of Industrial and Operations Engineering
University of Michigan
ebyon@umich.edu
29