Sollecitazioni travi

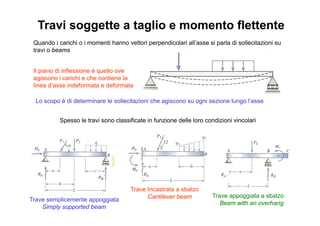
1. Travi soggette a taglio e momento flettente
Quando i carichi o i momenti hanno vettori perpendicolari all’asse si parla di sollecitazioni su
travi o beams
Il piano di inflessione è quello ove
agiscono i carichi e che contiene la
linea d’asse indeformata e deformata
Lo scopo è di determinare le sollecitazioni che agiscono su ogni sezione lungo l’asse
Trave Incastrata a sbalzo
Cantilever beam Trave appoggiata a sbalzo
Beam with an overhang
Trave semplicemente appoggiata
Simply supported beam
Spesso le travi sono classificate in funzione delle loro condizioni vincolari

2. Il passaggio dai vincoli fisici alla idealizzazione degli stessi nel modello va fatta
considerando le effettive condizioni di deformabilità locale
Il sistema di ancoraggio ad asola consente
piccoli spostamenti assiali carrello
Il fissaggio sulla parete sottile garantisce
l’impedimento della traslazione ma non la
locale rotazione cerniera
Il fissaggio rigido del piatto di base
garantisce il bloccaggio incastro
Le strutture a traliccio (travi sottili
rispetto ingombro struttura) sono
considerate come tutte incernierate
per effetto dei cedimenti vincolari –
dovuti anche a plasticità locale

3. In questo caso solo i tubi spessi lavorano a
flessioni e sostengono i carichi – i tubi sottili
mantengono la forma delle sezioni sotto carico
Versione completamente smontabile
Tipici giunti a molteplici innesti
Millennium bridge

4. CONCENTRATI: Se la zona di carico ha una piccola estensione
rispetto sviluppo assiale
In rapporto ai carichi applicati:
DISTRIBUITI: Se il carico è definito per unità di lunghezza q
q costante q variabile linearmente q(x) variabile in modo continuo
Calcolo delle reazioni vincolari
Sono immediatamente determinabili
solo per sistemi isostatici ai vincoli
esterni
pattino

5. Esempio di struttura composta:
Struttura piana a due aste rigide

6. DETERMINAZIONE DELLE FORZE DI TAGLIO E DEL MOMENTO
Il metodo prevede di applicare le condizioni di equilibrio al corpo
libero, ossia avendo sostituito ai vincoli le forze vincolari
Si effettua un taglio in una generica sezione x e si impone l’equilibrio (ds o sn)
0vertF   V x P
0xM   M x Px
CONVENZIONE DEI SEGNI (secondo deformabilità)
I momenti sono positivi quando le fibre inferiori sono tese
Il taglio è positivo quando provoca sul materiale rotazione oraria

7. Metodo dell’equilibrio differenziale
Si effettua l’equilibrio di un elementino fermandosi ai
termini dei I ordine
Eq. Verticale:
  0
dV
q x dx V V dx
dx
 
    
 
 
dV
q x
dx
 
Quindi la derivata del taglio coincide con l’intensità carico
distribuito, per il segno dipende dalla convenzione di V
Eq. Momento
    0
2
dx dM
M V x dx q x dx M dx
dx
 
     
 
 
dM
V x
dx

La derivata del momento flettente risulta pari all’azione del taglio V, il segno risulta dalle
convezioni adottate
Infinitesimo ord. superiore
Derivando la II e ricordando la I:
 
 
2
2
dV xd M
q x
dx dx
  
Assenza carico distribuito: taglio costante, momento
variabile linearmente
Carico distribuito costante: taglio lineare, momento
variabile quadraticamente
Carico distribuito potenza n: taglio potenza n+1,
momento potenza n+2
x polo eq.

8. DIAGRAMMI DEL TAGLIO E DEL MOMENTO FLETTENTE
La rappresentazione grafica è molto utile per determinare
le sezioni più sollecitate ove sarà opportuno effettuare le
verifiche strutturali
Calcolo reazioni vincolari
0AM 
2
0
2
B
L
R L Pa q   2
B
Pa L
R q
L
 
2
A
Pb L
R q
L
 
  0
( )
x
a A aM x M V x dx     0
0
2
x
a
Pb L
M x q qx dx
L
 
    
 

0 x a 
Tracciamento dei diagrammi
  0
( )
x
a AV x R q x dx    
2
a
Pb L
V x q qx
L
  
a x L 
    ( )
x
b a
a
V x V a P q x dx     
2
b
Pa L
V x q qx
L
   
   
2
2
( )
2 2 2 2
x
x
b a ba
a
Pab aL q Pax Lx qx
M x M a V x dx q a q
L L
  
           
   

  2
2 2
a
Pb L q
M x q x x
L
 
   
 
 0 0aM 
 
2 2
2 2
b
Pab Pa Pax Lx qx
M x q
L L L
       0bM L 

9.  
2
b
Pa L
V x q qx
L
   a x L 
0 x a    2
2 2
a
Pb L q
M x q x x
L
 
   
 
Andamento del momento
Posto dalla parte fibre tese
 
2
a
Pb L
V x q qx
L
  0 x a 
2
A
Pb L
R q
L
 
Andamento del taglio
2
Pa L
q
L
 


2
B
Pa L
R q
L
 
2
Pb L
q
L

 0 0aM 
Nelle posizioni estremali:
 
2
a
P q
M a ab
L
 
  
 
Cerchiamo il massimo
all’interno del campo:
  0
2
a
Pb qL
M x qx
L
      
 
max
2
A
Pb L
x
qL
 
 
2
max
2 2
a A
q Pb L
M x
qL
 
  
 
Il massimo è in x=a se max
2
A
Pb L
x a
qL
  

10. Andamento del momento a x L 
Posto dalla parte fibre tese
 
2
b
P q
M a ab
L
 
  
 
Nelle posizioni estremali:
  0bM L 
max
2
B
L Pa
x
qL
 
 
2
max
2 2
b B
q Pa L
M x
qL
 
  
 
Cerchiamo il massimo
all’interno del campo:
  0
2
b
Pa qL
M x qx
L
       
 
Il massimo è in x=a se max
2
B
L Pa
x a
qL
  
 
2 2
2 2
b
Pab Pa Pax Lx qx
M x q
L L L
    
Il valore massimo del momento tra 0 e L potrà assumere quindi uno dei seguenti valori
max
2
P q
M ab
L
 
  
 
2
max
2 2
q Pb L
M
qL
 
  
 
2
max
2 2
q Pa L
M
qL
 
  
 
maxse x a maxse x a maxse x a

11. Andamenti in altri Esempi

12. Strutture reticolari
Sia che si tratti di collegamenti
angolari, sia mediante perni, queste
strutture vengono schematizzate
mediante cerniere in quanto sotto
carico le giunzioni si comportano
come cerniere plastiche
Per verificare l’isostaticità occorre valutare i GdL. Per il loro calcolo risulta più agevole
considerare le cerniere come corpi rigidi e le aste (non si ha mai momento flettente se i
carichi sono applicati solo alle cerniere) come vincoli che sottraggono 1 GdL.
 2 numero di cerniereGdL      numero aste vincoli a terraGdV  
La struttura sarà iperstatica se GdV > GdL, isostatica se GdV = Gdl, ipostatica GdV < GdL
39 cerniere = 78 GdL
75 aste + 3 vincoli = 78 GdV
La struttura è isostatica e non è labile in
quanto composta da tanti anelli chiusi
isostatici e ben vincolata a terra

13. Se si stacca un’asta in corrispondenza di un nodo i sostituendo al vincolo interno i carichi,
l’equilibrio alla rotazione in j dell’asta i-j impone che sia nulla la componente ortogonale Ti
Pertanto gli elementi si comportano come bielle (se rettilinee
aste) essendo possibili solo carichi congiungenti i perni, di
trazione (tiranti) oppure di compressione (puntoni)
Data questa caratteristica le strutture reticolari sono particolarmente interessanti
perché carichi di trazione/compressione utilizzano pienamente le sezioni resistenti
Nel calcolo si ipotizza l’assenza dell’attrito nei perni

14. Classico traliccio alta tensione
Telaio motociclistico a culla
Chassis autoveicolo da competizione
misto reticolare – piastre portanti
Prima vettura a scocca portante

15. Esempio - Risoluzione mediante il metodo dell’equilibrio dei nodi
Il primo passo è spesso la risoluzione dei vincoli esterni
1 50 4 2M R P  
A ogni nodo si compongono vettorialmente le
forze esterne e quelle delle aste e si risolve per
una cerniera alla volta
5
1
2
R P
1vR P
1
2
o
P
R 
1vR
1oR
5R

16. Cern. E
6 cos 0
4 2
P
N
 
  
 
6 7sin 0
4
 
  
 
N N
6 7
2
;
2 2
 
P
N P N
Si possono già risolvere le aste 6 e 7, che subiscono azioni contrarie
rispetto a N6 e N7, e pertanto l’asta 6 è in compressione e la 7 in trazione.
5 4 cos 0
4
N N
 
  
 
4 7sin 0
4
N N
 
   
 
5 4
2
;
2 2
P
N N P 
Considerando i versi impostati per N5 e N4 l’asta 5 è
compressa, la 4 tesa
Cern. C scelta perché sia minimo il numero di incognite

17. 2 5 6cos cos 0
4 4
    
     
   
N N N
2 2N P
2
2 2 2
0
2 2 2 2
  
P
N P
2 3 6sin sin 0
4 4
    
      
   
N N N P
3
2

P
N
3
2 2 2
2 0
2 2 2
   P N P P
Considerando i versi impostati per N2 e N3, entrambe le aste 2 e 3 sono in compressione
Cern. D
1
2

P
N
L’ultima asta 1 si
trova in trazione
Cern. B Cern. A
L’ultima cerniera non ha incognite
e può essere utilizzata per verifica

18. Con carico P = 1 kN
Trazione
Compressione