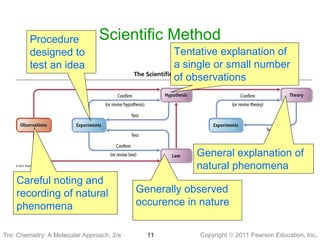
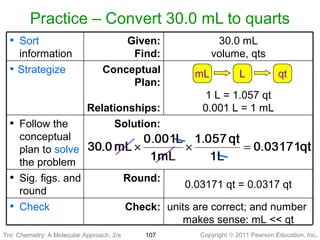
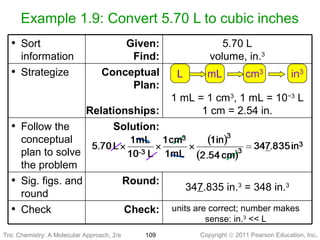
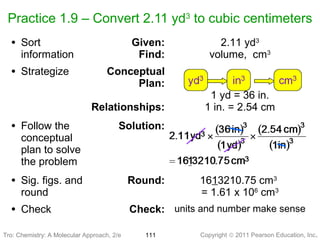
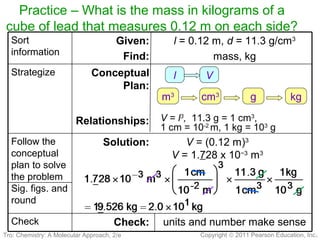
1) The document discusses the scientific method and how it is used to classify and understand matter through careful observation, hypothesis testing, and developing general theories.
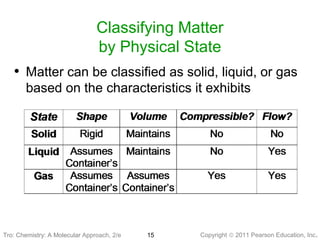
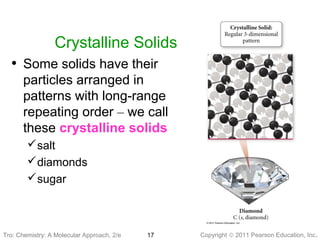
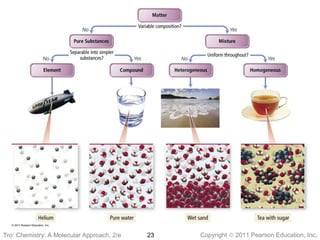
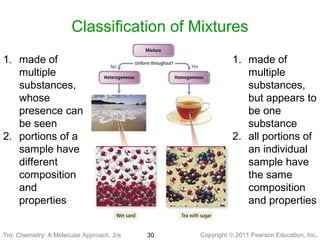
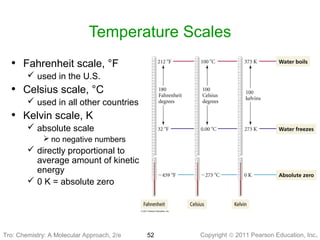
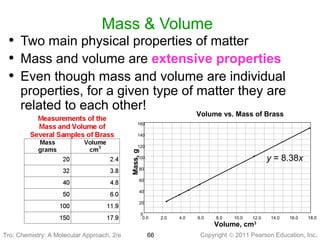
2) Matter can be classified based on its physical state as solid, liquid, or gas, which is determined by the structure and motion of atoms and molecules. It can also be classified based on its composition as pure substances like elements and compounds, or mixtures.
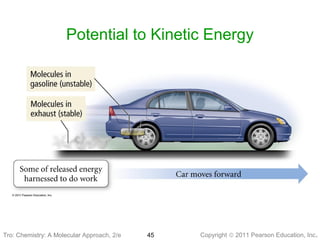
3) Changes in matter can be physical changes that alter state but not composition, or chemical changes that alter composition through rearrangement of atoms. Both types of changes are associated with gains or losses of energy.