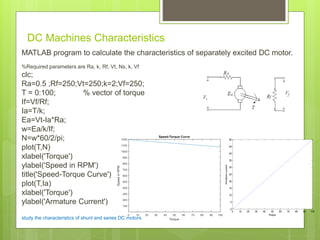
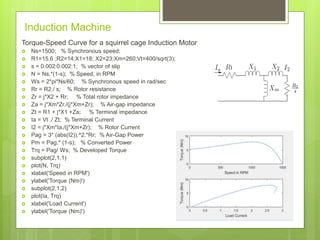
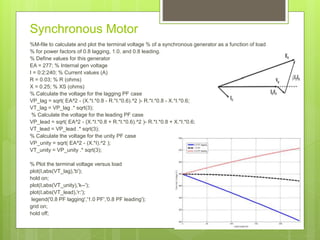
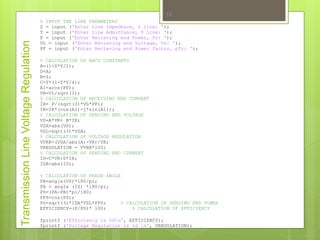
The document presents MATLAB sample scripts focusing on electrical engineering applications. It includes programs for calculating building height, BMI, electricity bills, and analyzing circuit characteristics. Various applications such as RLC circuit current vs frequency plots and synchronous motor voltage calculations are also discussed.

1. MATLAB Sample
Scripts
With Electrical Engineering
Applications
Shameer A Koya

2. Introduction
 This lecture we will do some practice on Basic
MATLAB Scripts.
 We will start with simple scripts and will discuss
some electrical engineering applications.
 More scripts including conditional statements will
be discussed in the next lecture.
 Please review lectures on basic input and output
commands.

3. Script 1
% Program to calculate Height of a Building
from time a stone takes to reach the basement.
% Use g=9.81and k=0.05
g=9.81;
k=0.05;
time= input (‘Enter the time taken: ‘);
height=g*(time+(exp(-k*time)-1)/k)/k;
disp(’Depth of well is ’)
disp(depth)
disp(’metres’)

4. Script 2
% Program to calculate the BMI (body mass index)
% Input your Height and Weight
weight = input('Type your weight (kg): ');
height = input('Type your height (m): ');
bmi = weight / height^2;
% Display the BMI
fprintf('Your Body Mass Index is %fn", bmi);

5. Script 3
% Program to calculate Electricity bill.
w = input('Enter power of your device (in watts):
');
h = input('Enter time (in hours): ');
r = input('Enter electricity rate (in dollars per
KWH): ');
ec = w * h/1000 * r;
disp(’Your Electricity bill is’)
Disp(ec)

6. Power transfer vs Load resistance curve
RL = 1:0.01:10;
Vs = 12;
Rs = 2.5;
P = (Vs^2*RL)./(RL+Rs).^2;
plot(RL,P)
xlabel('Load resistance')
ylabel('Power dissipated')
1 2 3 4 5 6 7 8 9 10
9
10
11
12
13
14
15
Load resistance
Powerdissipated

7. Curve fitting
% Second order curve fitting
%enter the input x and y vectors
x = [0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1];
y = [-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
n = 2;
p = polyfit( x, y, n ) %Find the best quadratic fit to the
data
xi = linspace(0,1,100);
yi = polyval(p, xi); % evaluate the polynomial
plot(x,y,’-o’, xi, yi, ‘-’)
xlabel(‘x’), ylabel(‘y = f(x)’)
title(‘Second Order Curve Fitting Example’)

8. Series RLC circuit
 % Program to plot current vs frequency semilog plot of a
series RLC circuit
 R = input('Enter value of resistance in ohms:');
 L = input('Enter value of inductance in Henary:');
 C = input('Enter value of capacitance in Farads:');
 V = input('Supply voltage in volts:')
 f = 0 : 1: 1000000;
 XL = 2 * pi .* f * L;
 XC = 1./(2 * pi .* f * C);
 Z = (R^2-(XL-XC).^2).^0.5;
 I = V ./ Z;
 semilogx(f,real(I));
 title('Current Vs Log frequency plot' );
 xlabel('fLogf');
 ylabel('Current in A');
8

9. DC Machines Characteristics
MATLAB program to calculate the characteristics of separately excited DC motor.
%Required parameters are Ra, k, Rf, Vt, Ns, k, Vf
clc;
Ra=0.5 ;Rf=250;Vt=250;k=2;Vf=250;
T = 0:100; % vector of torque
If=Vf/Rf;
Ia=T/k;
Ea=Vt-Ia*Ra;
w=Ea/k/If;
N=w*60/2/pi;
plot(T,N)
xlabel('Torque')
ylabel('Speed in RPM')
title('Speed-Torque Curve')
plot(T,Ia)
xlabel('Torque')
ylabel('Armature Current')
study the characteristics of shunt and series DC motors
0 10 20 30 40 50 60 70 80 90 100
0
5
10
15
20
25
30
35
40
45
50
Torque
Armaturecurrent

10. Induction Machine
Torque-Speed Curve for a squirrel cage Induction Motor
 Ns=1500; % Synchronous speed;
 R1=15.6 ;R2=14;X1=18; X2=23;Xm=260;Vt=400/sqrt(3);
 s = 0.002:0.002:1; % vector of slip
 N = Ns.*(1-s); % Speed, in RPM
 Ws = 2*pi*Ns/60; % Synchronous speed in rad/sec
 Rr = R2./ s; % Rotor resistance
 Zr = j*X2 + Rr; % Total rotor impedance
 Za = j*Xm*Zr./(j*Xm+Zr); % Air-gap impedance
 Zt = R1 + j*X1 +Za; % Terminal impedance
 Ia = Vt ./ Zt; % Terminal Current
 I2 = j*Xm*Ia./(j*Xm+Zr); % Rotor Current
 Pag = 3* (abs(I2)).^2.*Rr; % Air-Gap Power
 Pm = Pag.* (1-s); % Converted Power
 Trq = Pag/ Ws; % Developed Torque
 subplot(2,1,1)
 plot(N, Trq)
 xlabel('Speed in RPM')
 ylabel('Torque (Nm)')
 subplot(2,1,2)
 plot(Ia, Trq)
 xlabel('Load Current')
 ylabel('Torque (Nm)')

11. Synchronous Motor
%M-file to calculate and plot the terminal voltage % of a synchronous generator as a function of load
% for power factors of 0.8 lagging, 1.0, and 0.8 leading.
% Define values for this generator
EA = 277; % Internal gen voltage
I = 0:2:240; % Current values (A)
R = 0.03; % R (ohms)
X = 0.25; % XS (ohms)
% Calculate the voltage for the lagging PF case
VP_lag = sqrt( EA^2 - (X.*I.*0.8 - R.*I.*0.6).^2 )- R.*I.*0.8 - X.*I.*0.6;
VT_lag = VP_lag .* sqrt(3);
% Calculate the voltage for the leading PF case
VP_lead = sqrt( EA^2 - (X.*I.*0.8 + R.*I.*0.6).^2 )- R.*I.*0.8 + X.*I.*0.6;
VT_lead = VP_lead .* sqrt(3);
% Calculate the voltage for the unity PF case
VP_unity = sqrt( EA^2 - (X.*I).^2 );
VT_unity = VP_unity .* sqrt(3);
% Plot the terminal voltage versus load
plot(I,abs(VT_lag),'b');
hold on;
plot(I,abs(VT_unity),'k--');
plot(I,abs(VT_lead),'r:');
legend('0.8 PF lagging','1.0 PF','0.8 PF leading');
grid on;
hold off;

12. TransmissionLineVoltageRegulation
12
% INPUT THE LINE PARAMETERS
Z = input ('Enter Line Impedence, Z line: ');
Y = input ('Enter Line Admittance, Y line: ');
P = input ('Enter Recieving end Power, Pr: ');
VL = input ('Enter Recieving end Voltage, Vr: ');
PF = input ('Enter Recieving end Power factor, pfr: ');
% CALCULATION OF ABCD CONSTANTS
A=(1+Z*Y/2);
D=A;
B=Z;
C=Y*(1+Z*Y/4);
A1=acos(PF);
VR=VL/sqrt(3);
% CALCULATION OF RECEIVING END CURRENT
IR= P/(sqrt(3)*VL*PF);
IR=IR*(cos(A1)-j*sin(A1));
% CALCULATION OF SENDING END VOLTAGE
VS=A*VR+ B*IR;
VSA=abs(VS);
VSL=sqrt(3)*VSA;
% CALCULATION OF VOLTAGE REGULATION
VVRR=(VSA/abs(A)-VR)/VR;
VREGULATION = VVRR*100;
% CALCULATION OF SENDING END CURRENT
IS=C*VR+D*IR;
ISA=abs(IS);
% CALCULATION OF PHASE ANGLE
PA=angle(VS)*180/pi;
PB = angle (IS) *180/pi;
PS=(PA-PB)*pi/180;
PFS=cos(PS);
PS=sqrt(3)*ISA*VSL*PFS; % CALCULATION OF SENDING END POWER
EFFICIENCY=(P/PS)* 100; % CALCULATION OF EFFICIENCY
fprintf ('Efficiency is %dn', EFFICIENCY);
fprintf ('Voltage Regulation is %d n', VREGULATION);