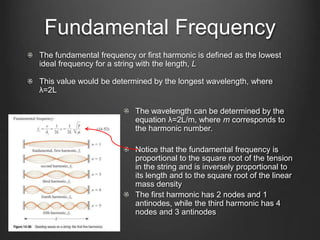
This document discusses standing waves on strings. It defines key terms like nodes and antinodes. The fundamental frequency is the lowest frequency for a string of length L, and is determined by the longest wavelength of λ=2L. Examples are given to calculate the wave speed, number of reflections in a time period, and frequencies of different harmonics. The fundamental frequency is directly proportional to the square root of the tension and inversely proportional to the length and square root of the linear mass density. Decreasing the tension decreases the fundamental frequency.

1. Standing Waves on
Strings
Learning Objective 2
Physics 101
Section LF2
By Shaireen Cassamali

2. Introduction
When working with a standing wave on a string, we are considering
the length, L, of the string with fixed ends
An ideal vibrating string will vibrate with its fundamental frequency
At the ends of the string where the amplitude is zero, we have a string
that can oscillate in a standing wave with the following wavelengths:
λ=2L/m, m = 1,2,3,4…
Length, L

3. Nodes and Antinodes
Recall from Standing Waves that:
a point with zero amplitude which remains at rest at all times
are called nodes.
a point that moves with the maximum possible amplitude of
2A (a result due to the combination of two waves) are called
antinodes.

4. Fundamental Frequency
The fundamental frequency or first harmonic is defined as the lowest
ideal frequency for a string with the length, L
This value would be determined by the longest wavelength, where
λ=2L
The wavelength can be determined by the
equation λ=2L/m, where m corresponds to
the harmonic number.
Notice that the fundamental frequency is
proportional to the square root of the tension
in the string and is inversely proportional to
its length and to the square root of the linear
mass density
The first harmonic has 2 nodes and 1
antinodes, while the third harmonic has 4
nodes and 3 antinodes

5. Try an Example
(page 227)
A guitar string is 0.46m long and has a linear mass density
of 2.98e-4kg/m. The tension in the string is kept at 80.0N
A) What is the wave speed?
B)If the string is plucked and allowed to vibrate,
approximately how many times would a wave reflect from
one end of the string in 3 seconds
C)What are the wavelengths and the frequencies for the
first 2 normal modes and the 4th normal mode of vibration
of the string?
D) How can we decrease the fundamental frequency?

6. Example Solution
A) The wave speed is determined by the tension and
linear mass density of the string:
v = √T/μ= √80.0N/2.98e-4kg/m = 518m/s
B) The time it takes for the waves to travel from one end of
the string to the other is:
t = length of the string/wave speed
= 0.46m/518m/s = 8.88e-4s

7. Solutions cont…
C) For the first harmonic: wavelength
= λ= 2L = 2(0.46) =0.92m
Frequency = v/λ = 518m/s / 0.92m = 563Hz
Second Harmonic: 2L/m = 2(0.46)/2 = 0.46m
Frequency = 518m/s / 0.42 = 1233Hz
Fourth Harmonic: 2L/4 = 2(0.46)/4 = 0.23m
Frequency = 518m/s / 0.23 = 2252Hz

8. Solutions cont...
D) In order to decrease the fundamental frequency, the
tension in the string must be decreased.
Recall:
f = (1/2L) (√T/μ)
f proportionate to √T
Decreasing the tension proportionately decreases the
frequency

9. FIN