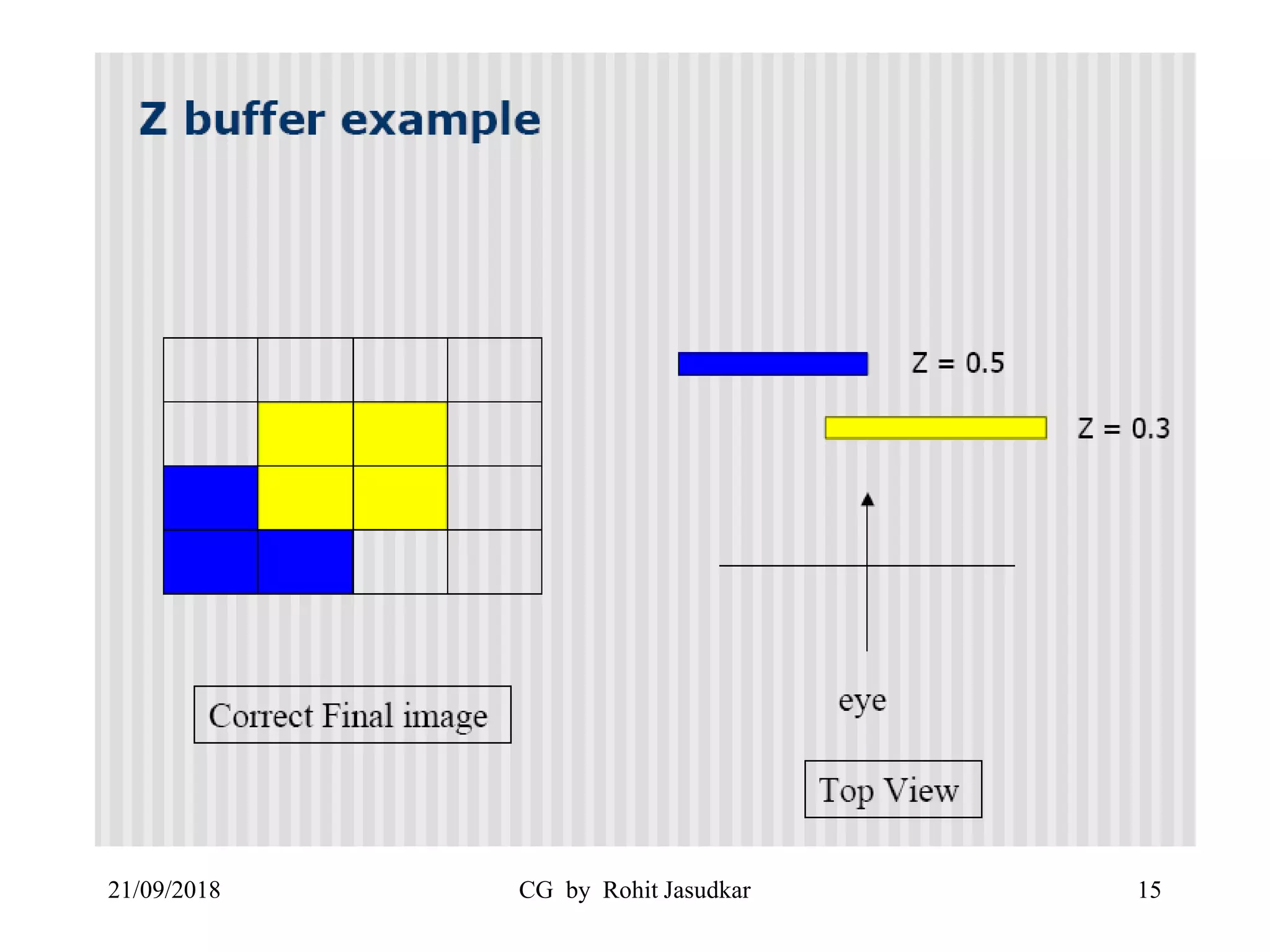
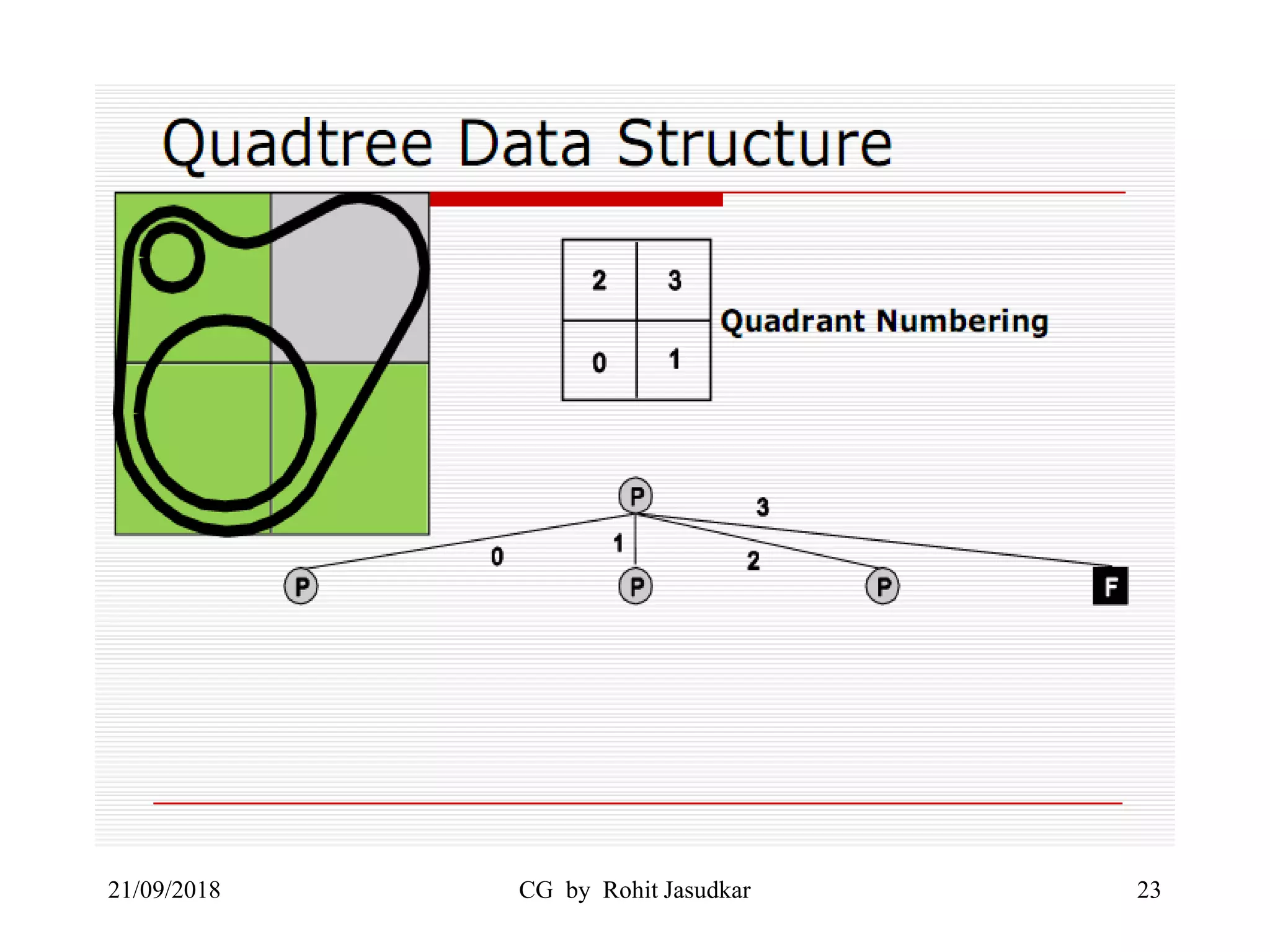
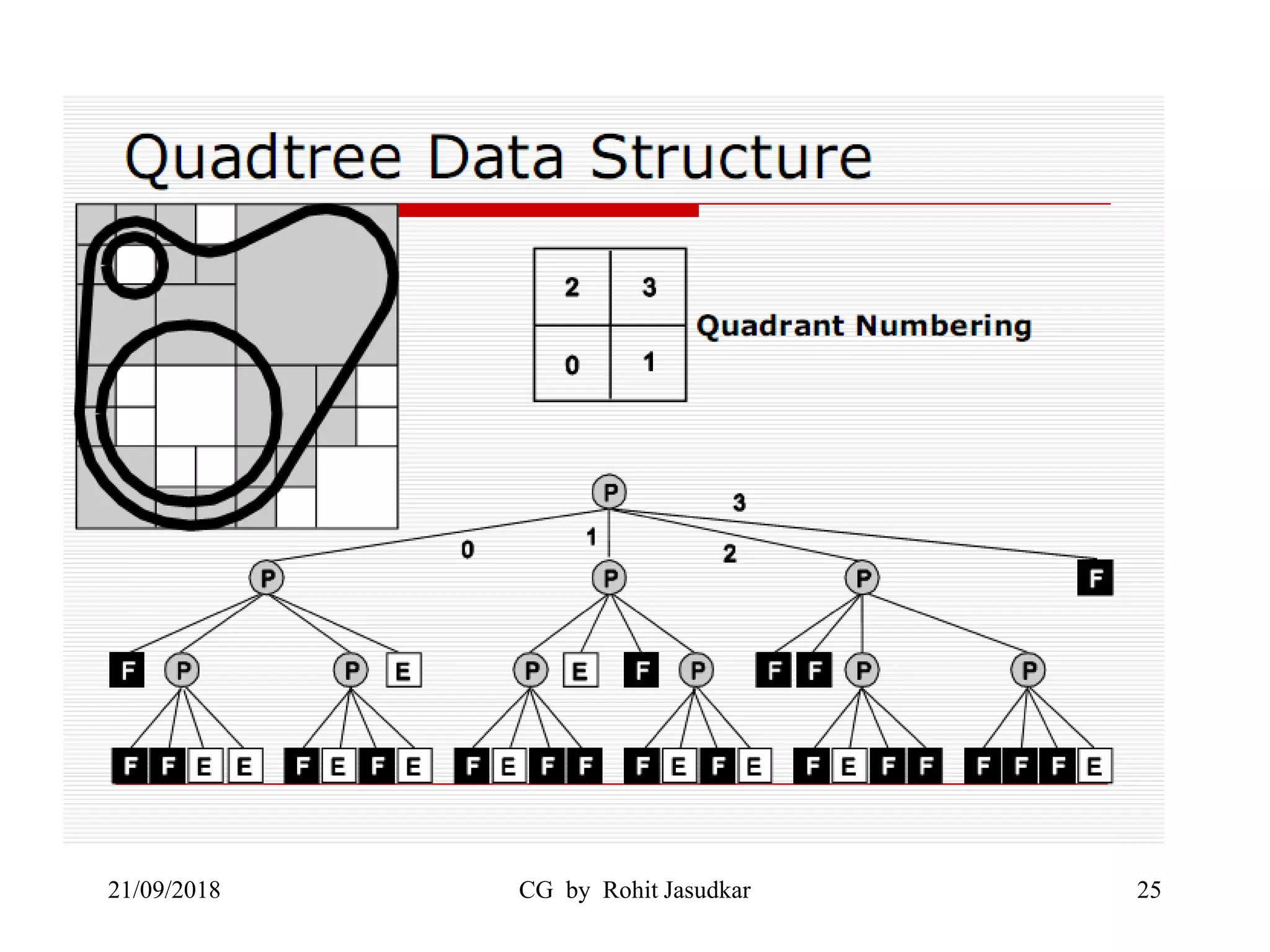
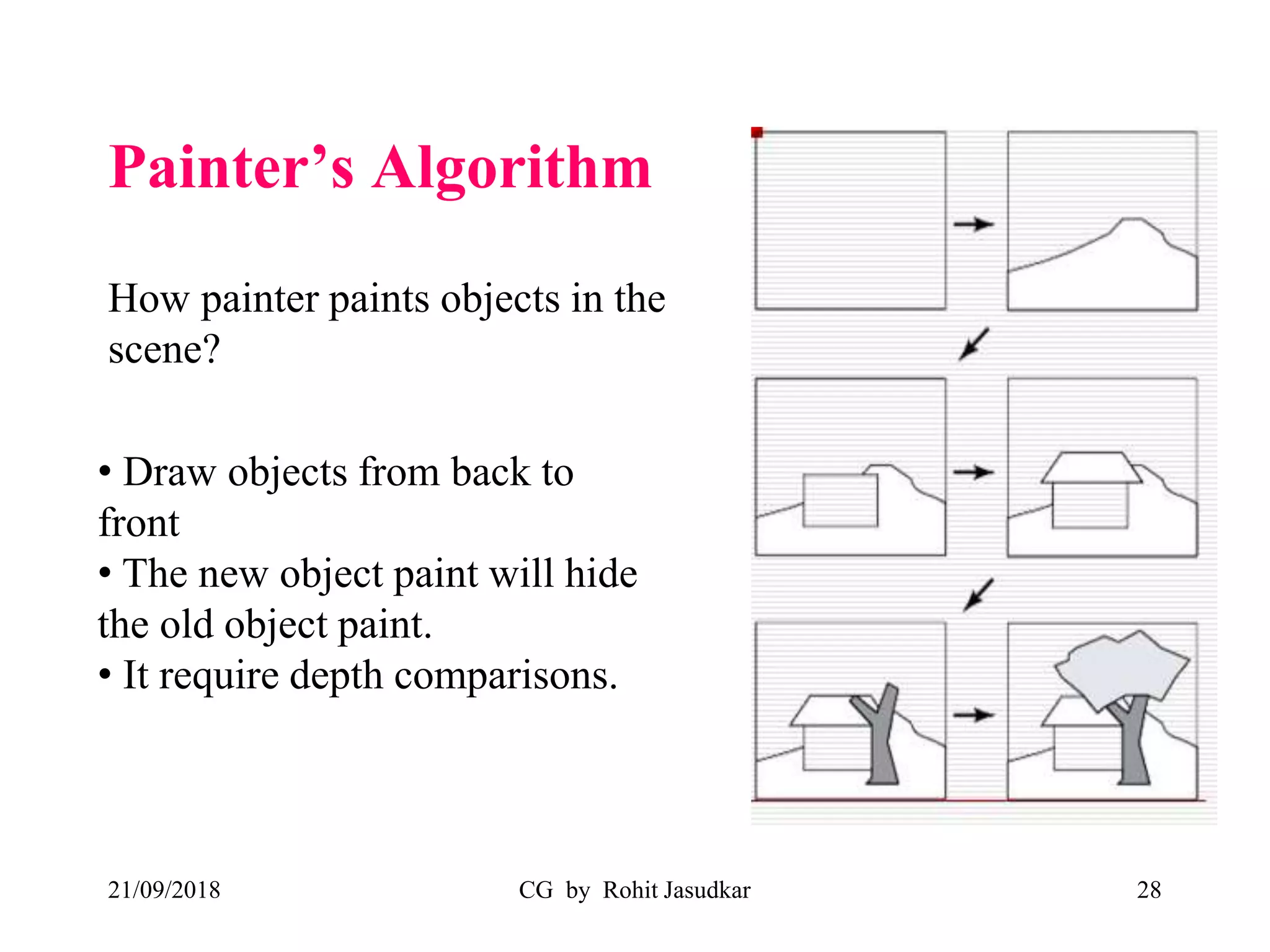
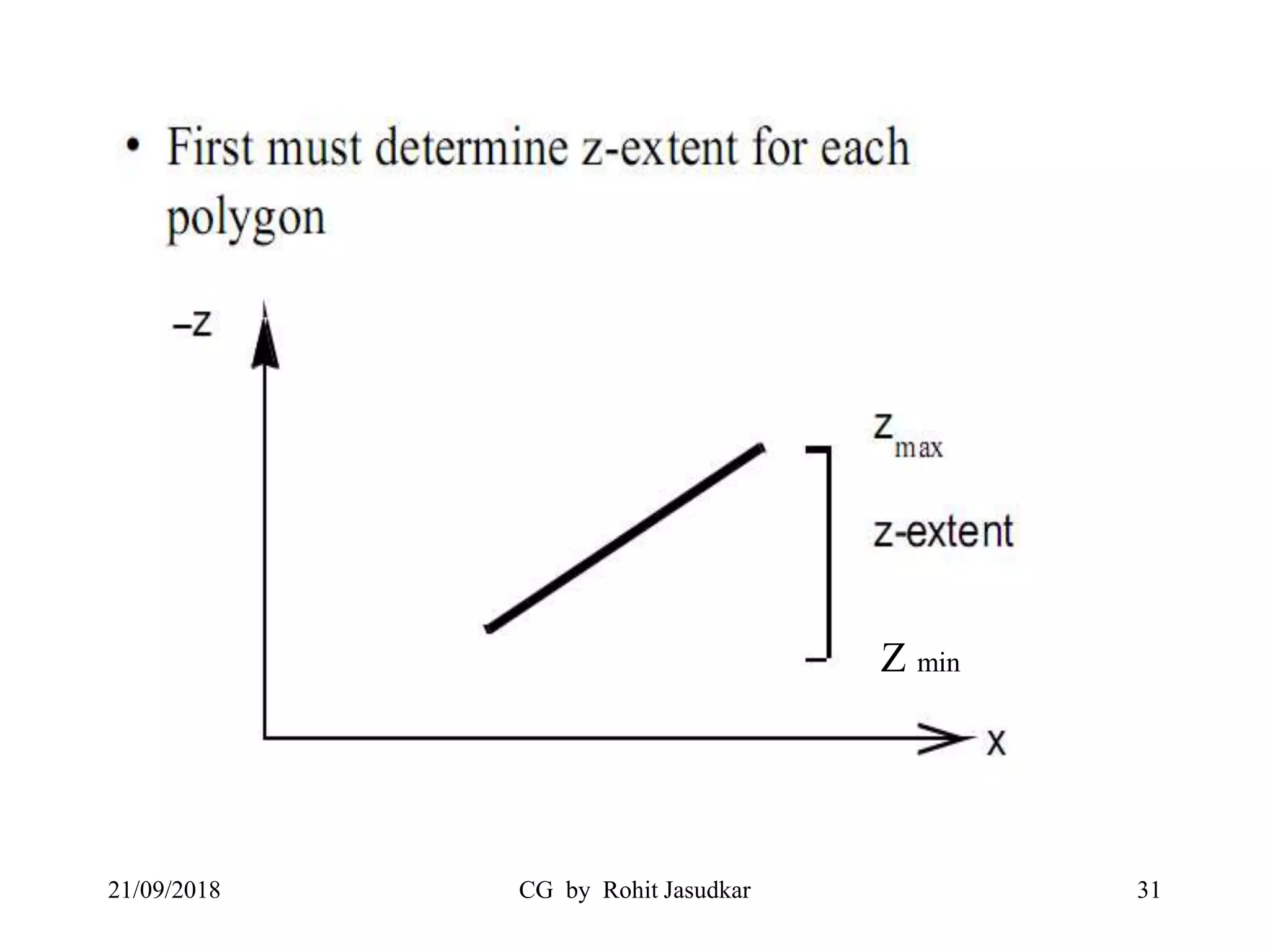
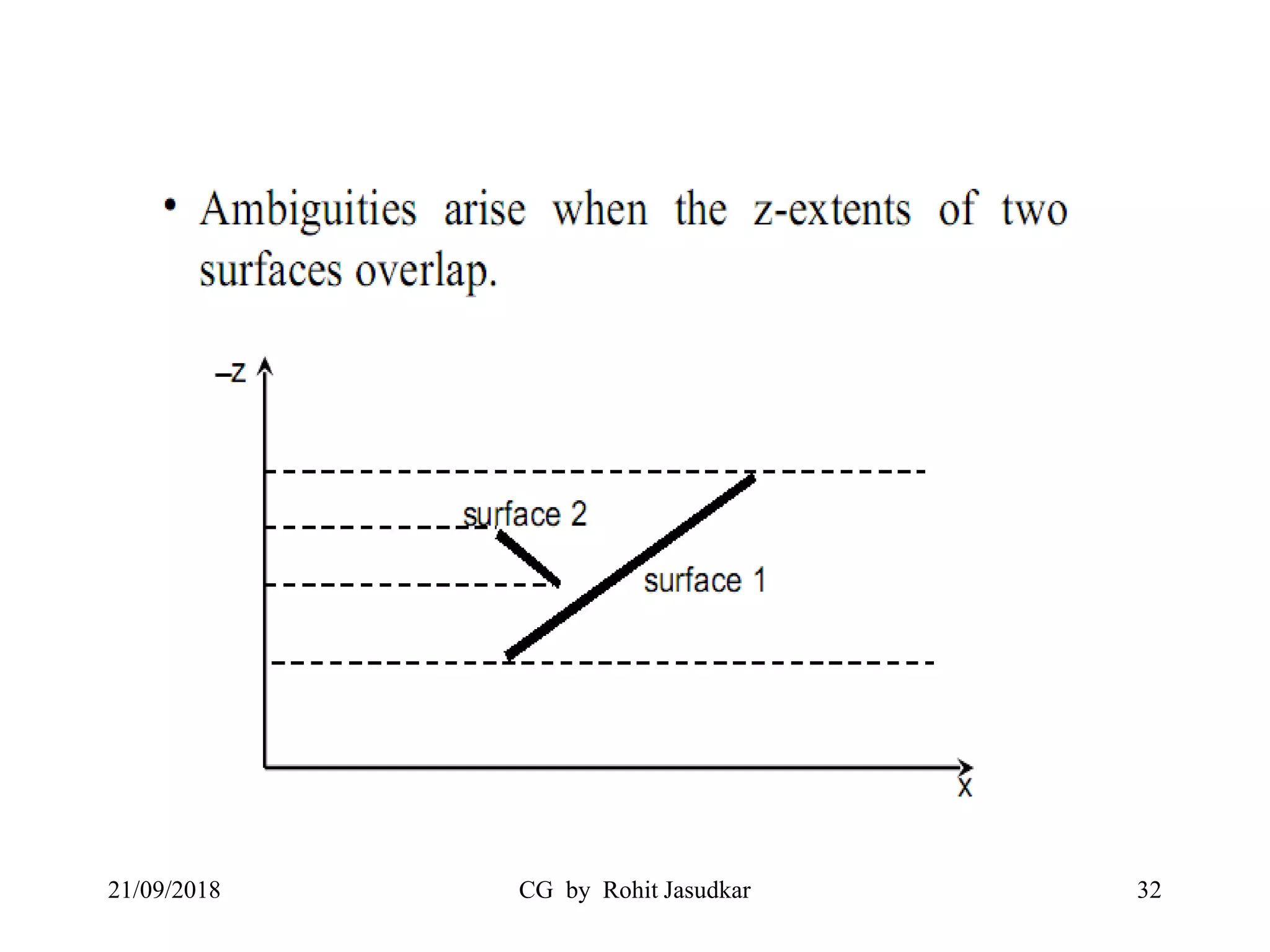
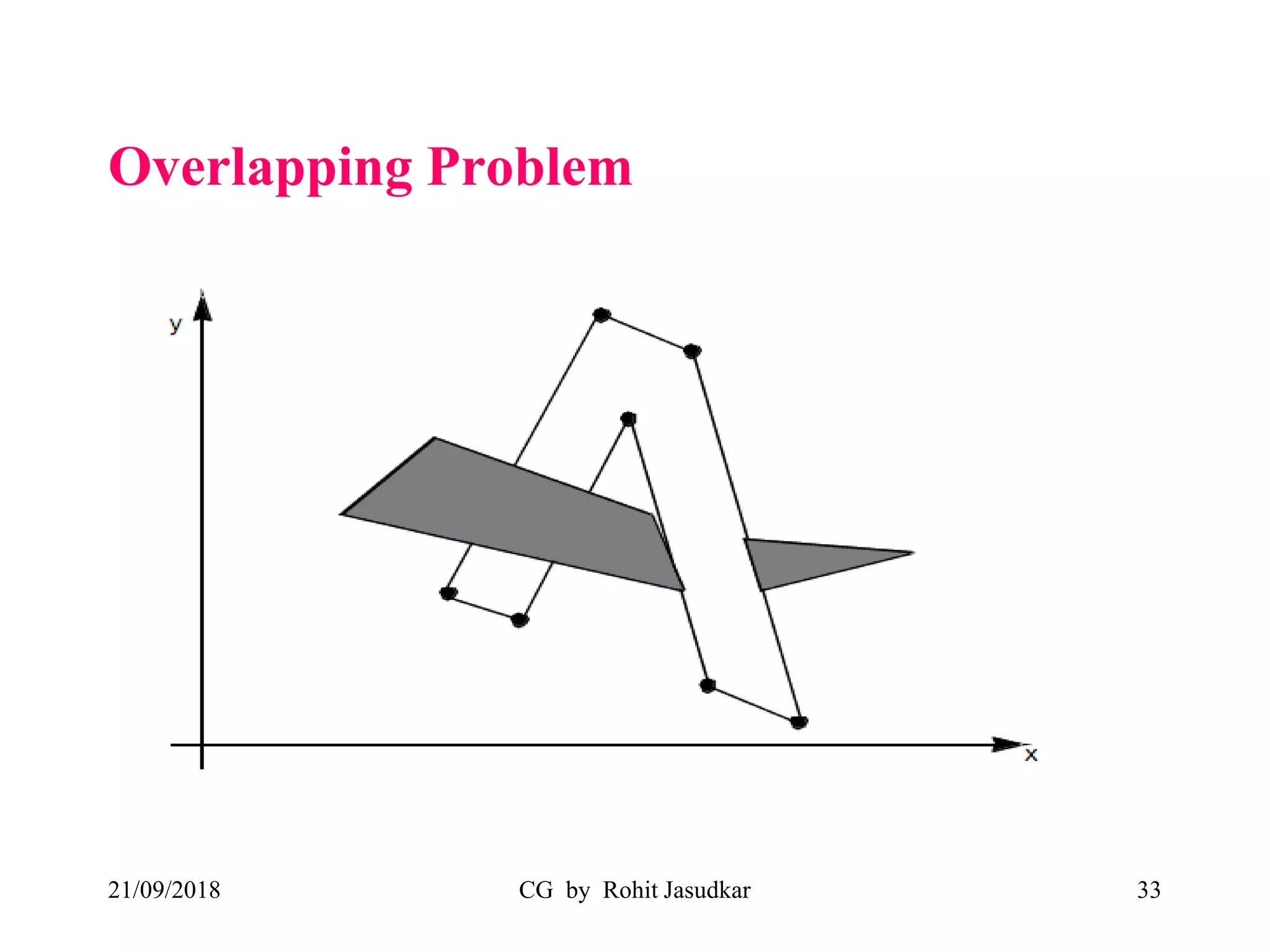
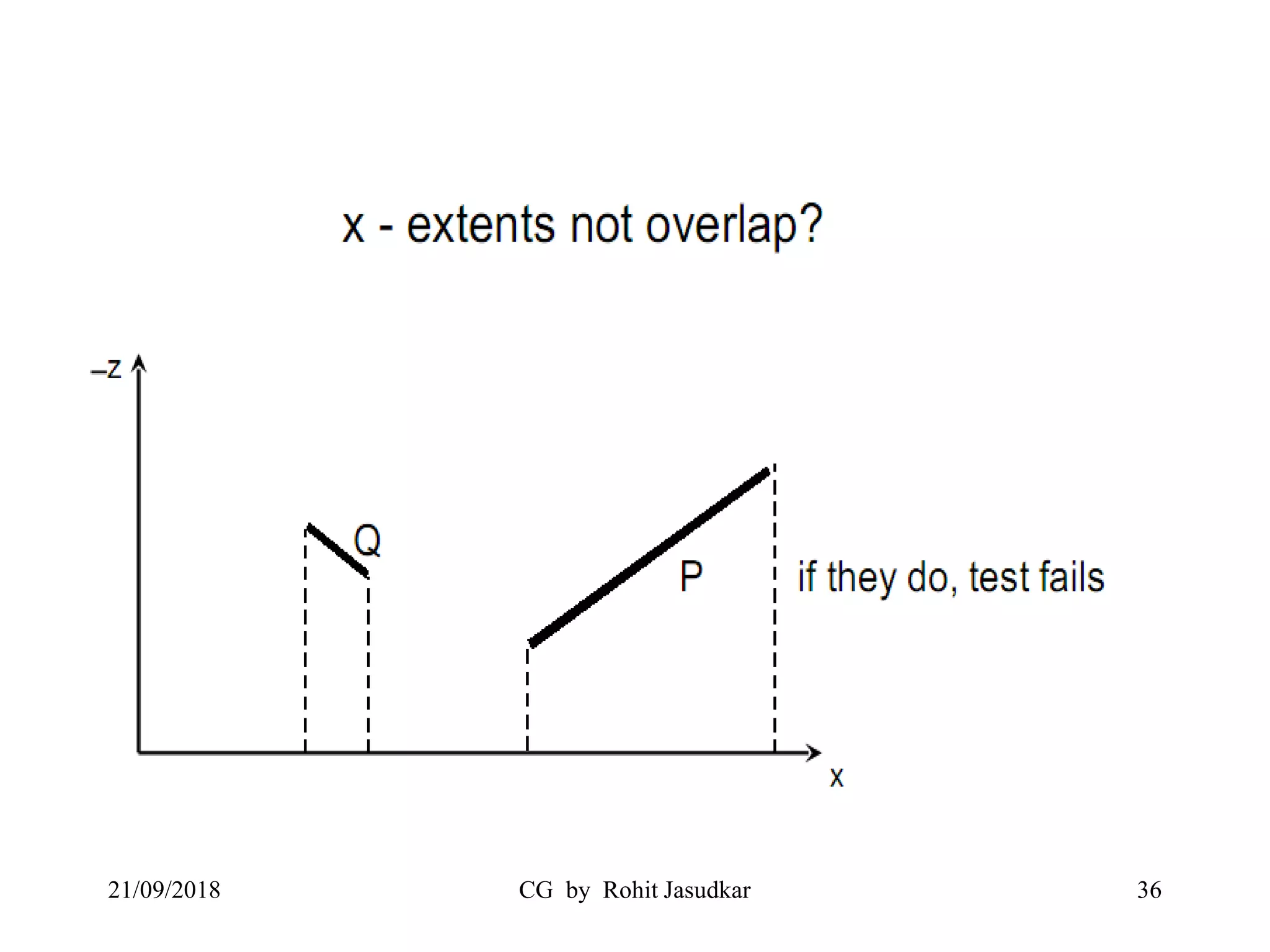
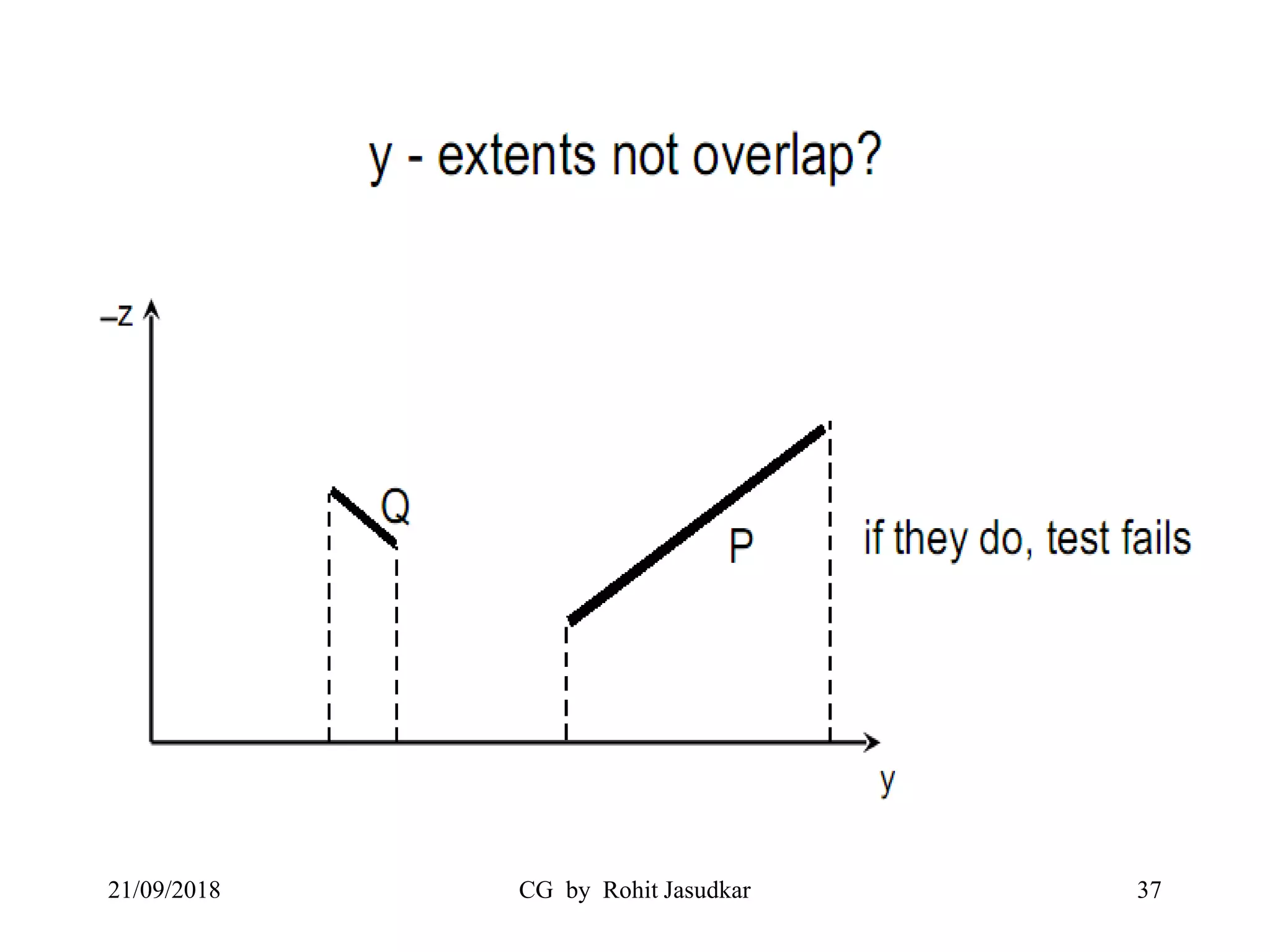
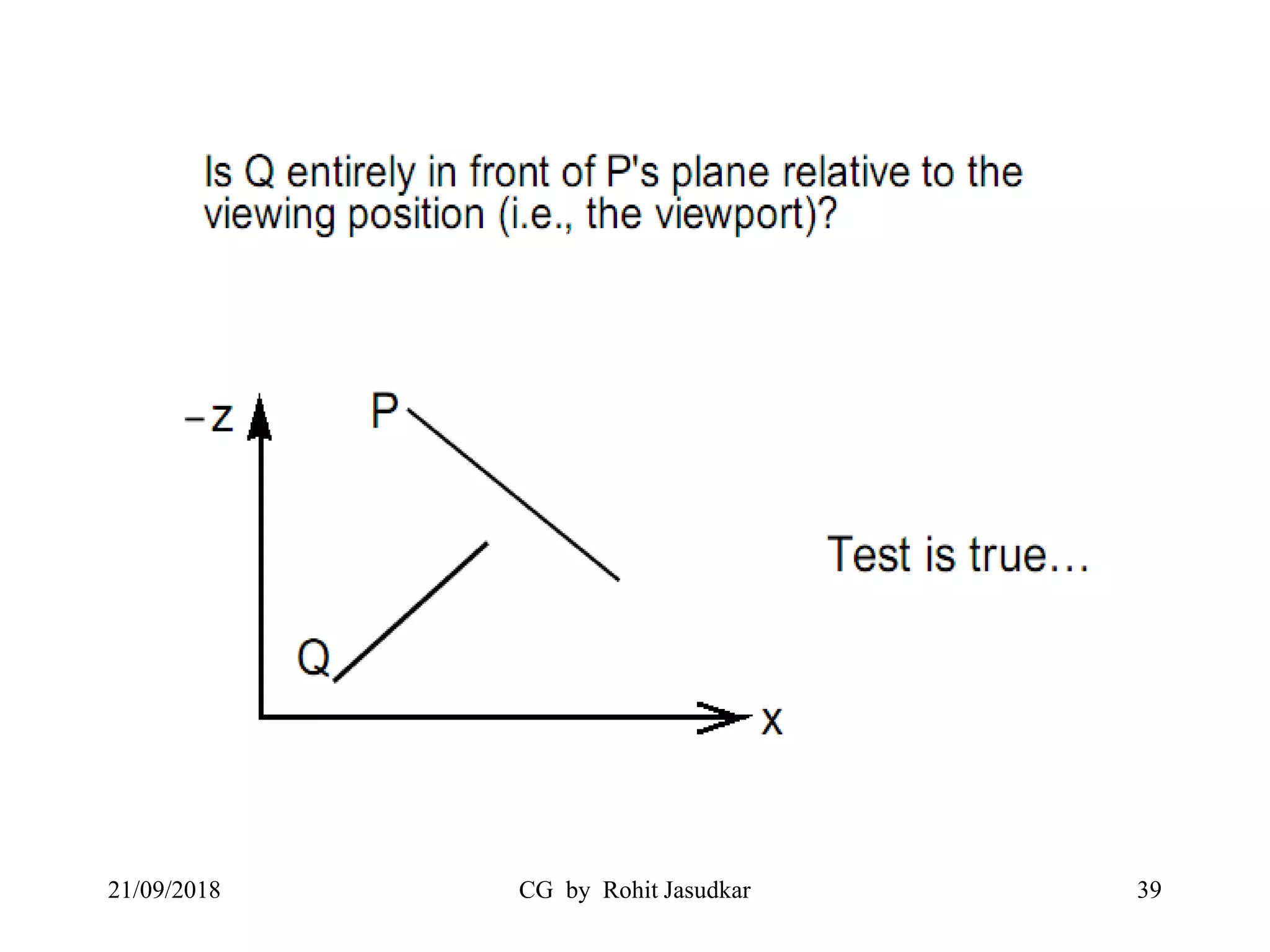
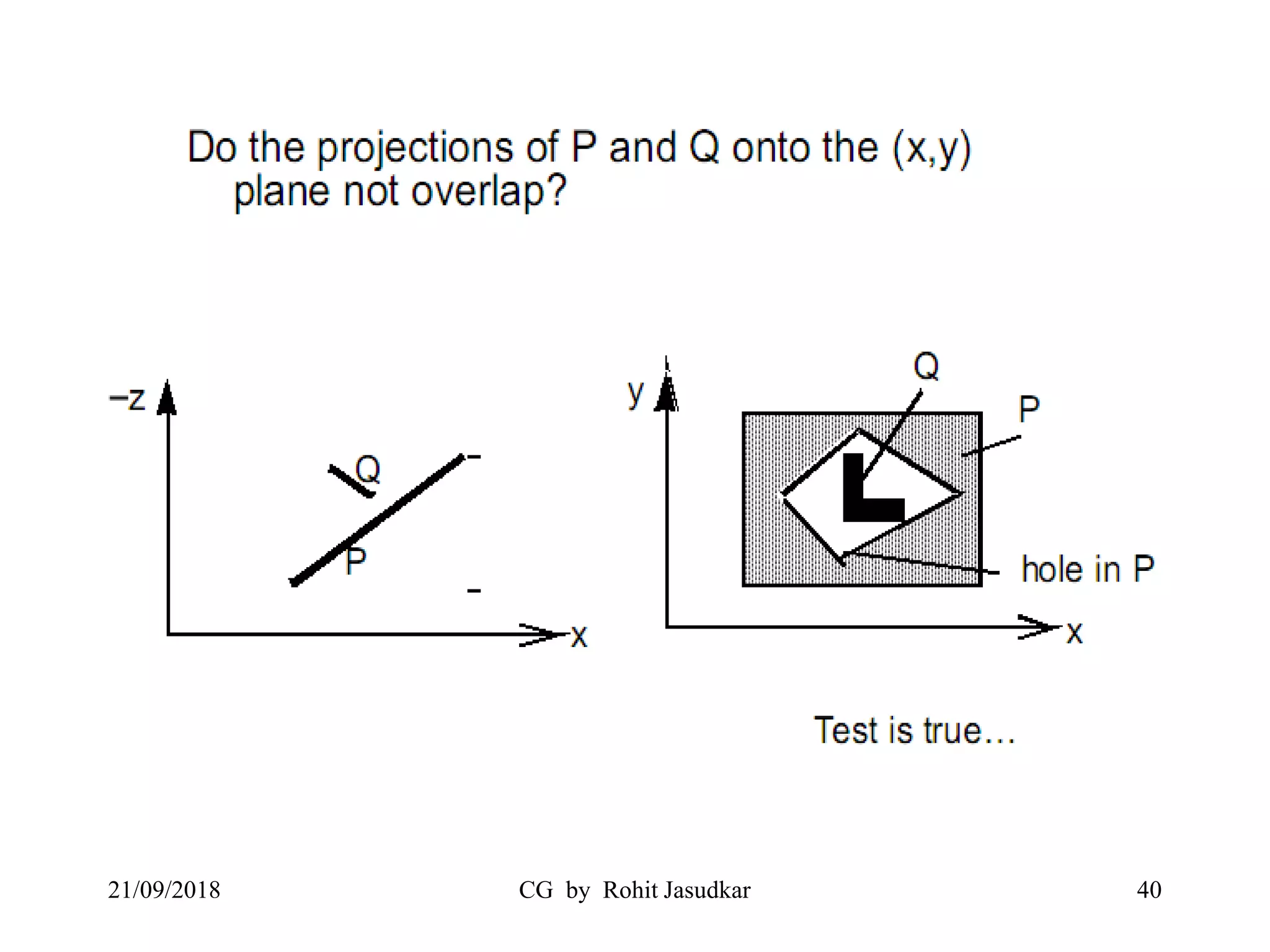
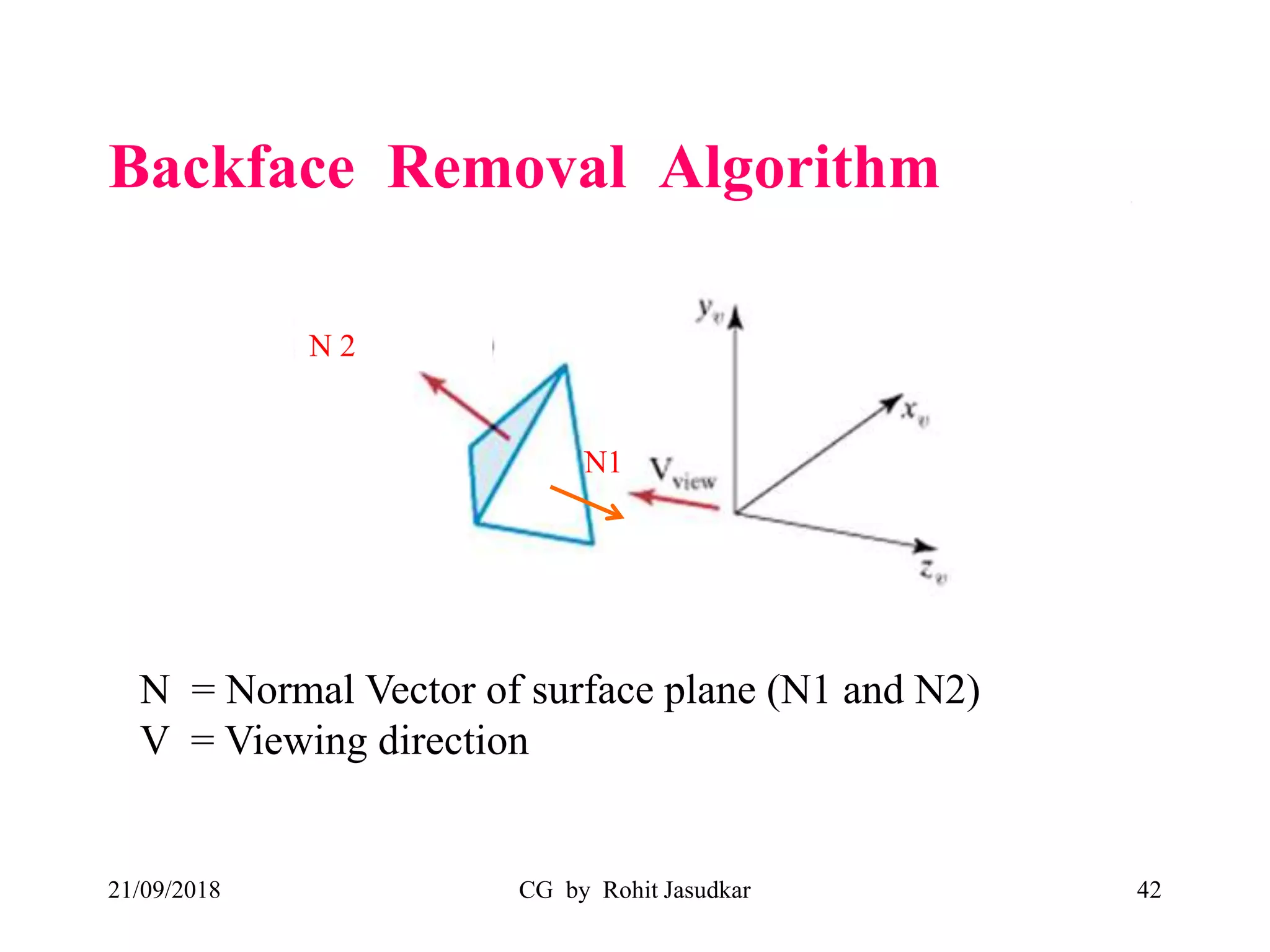
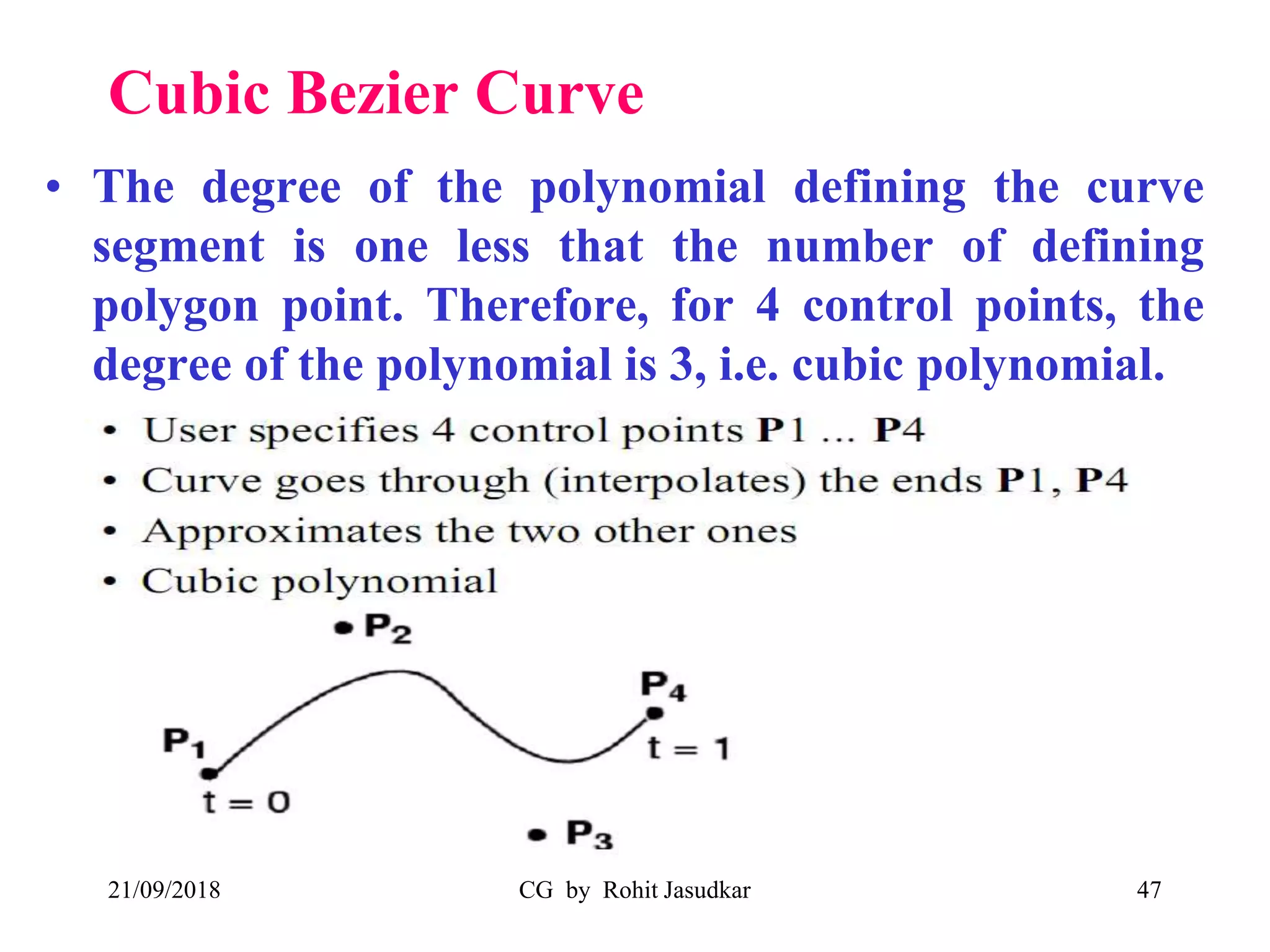
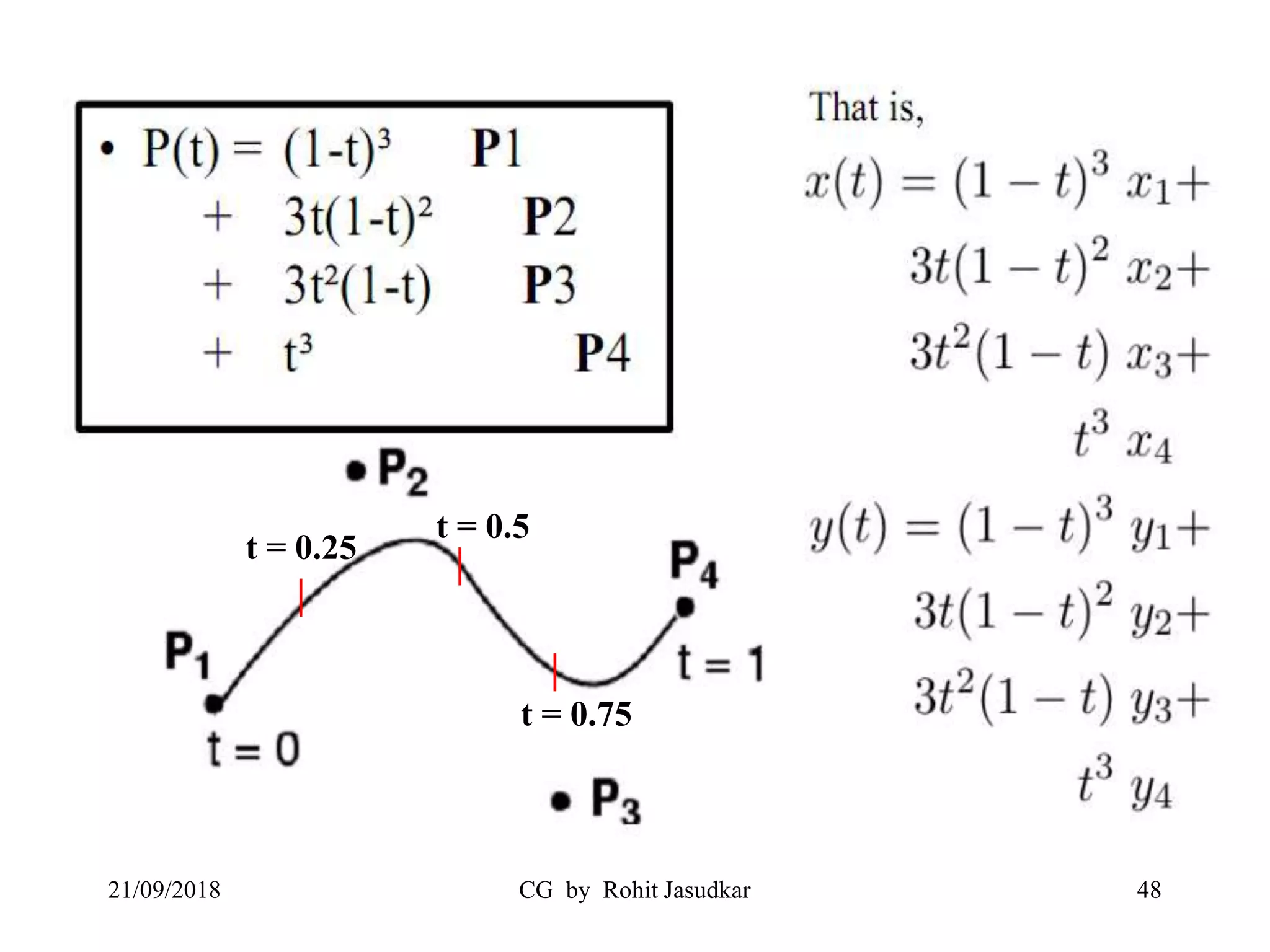
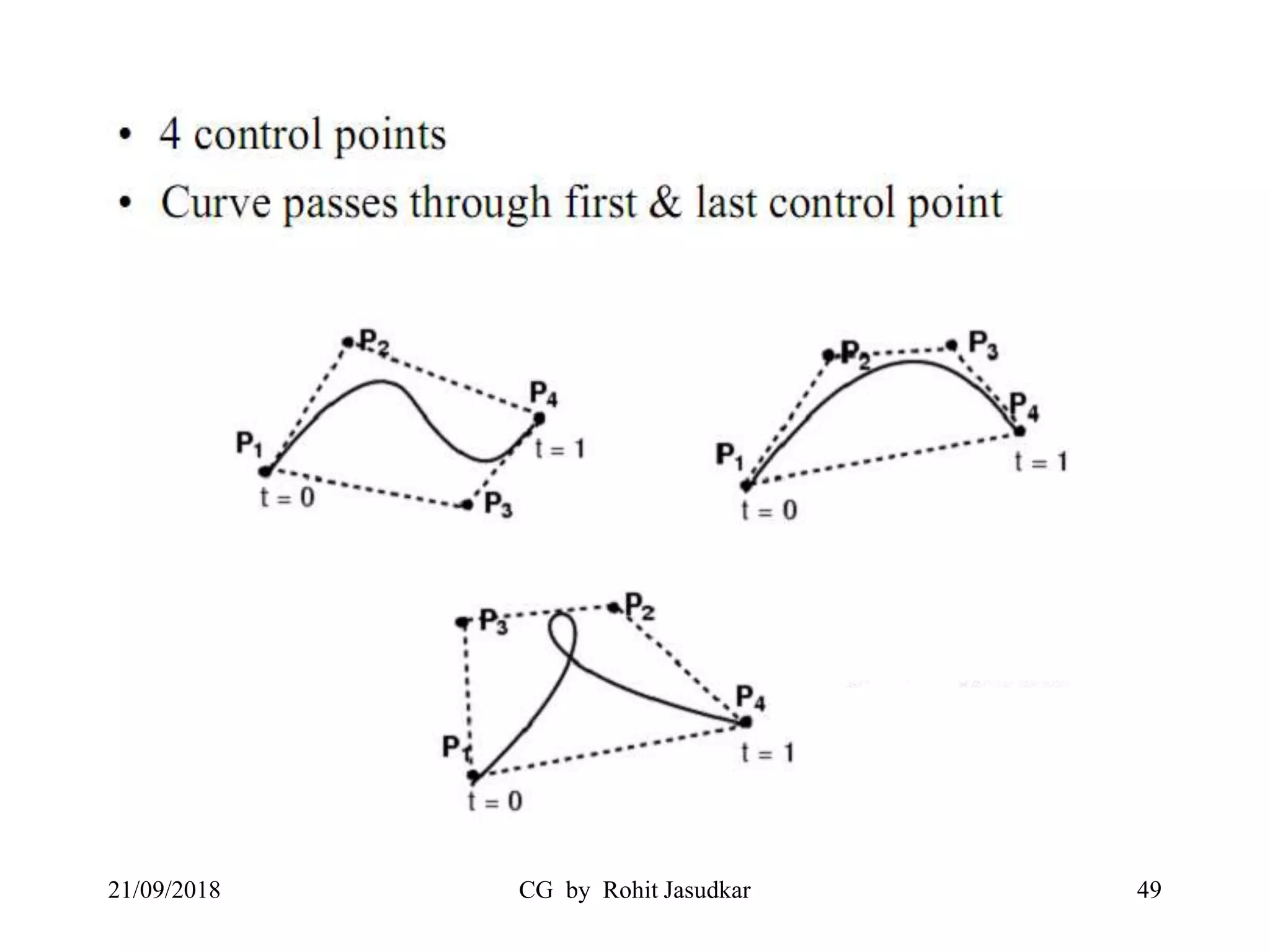
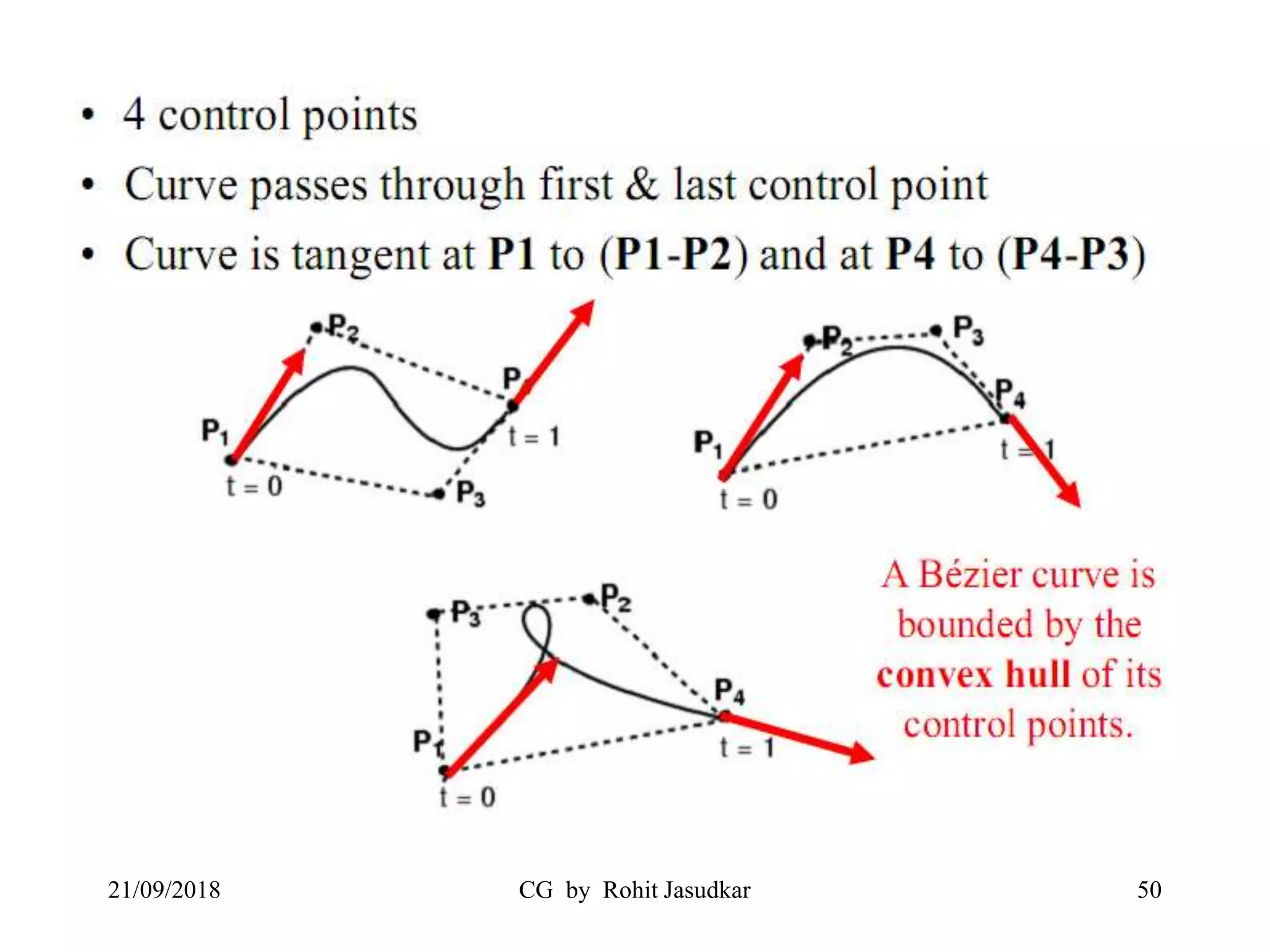
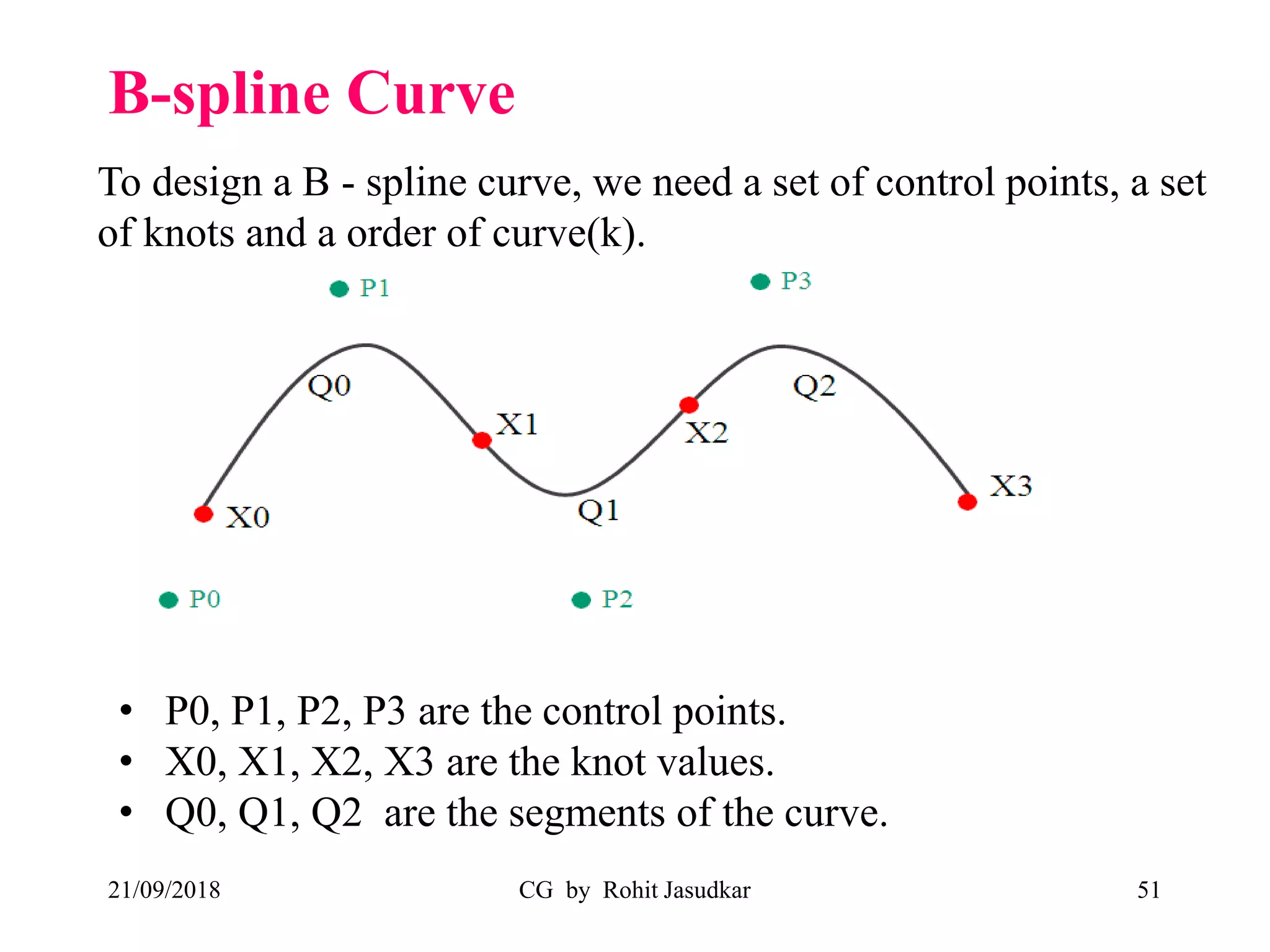
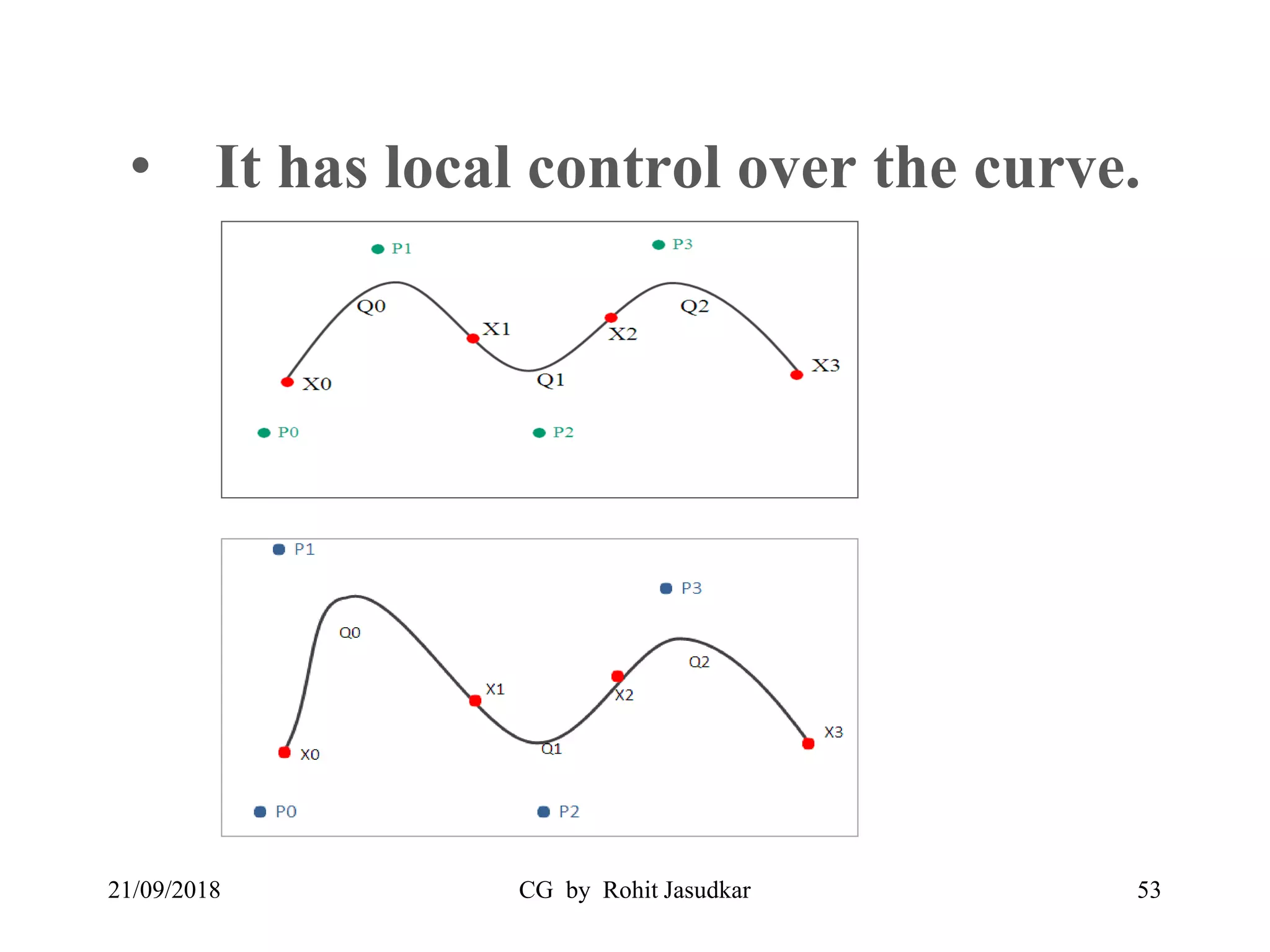
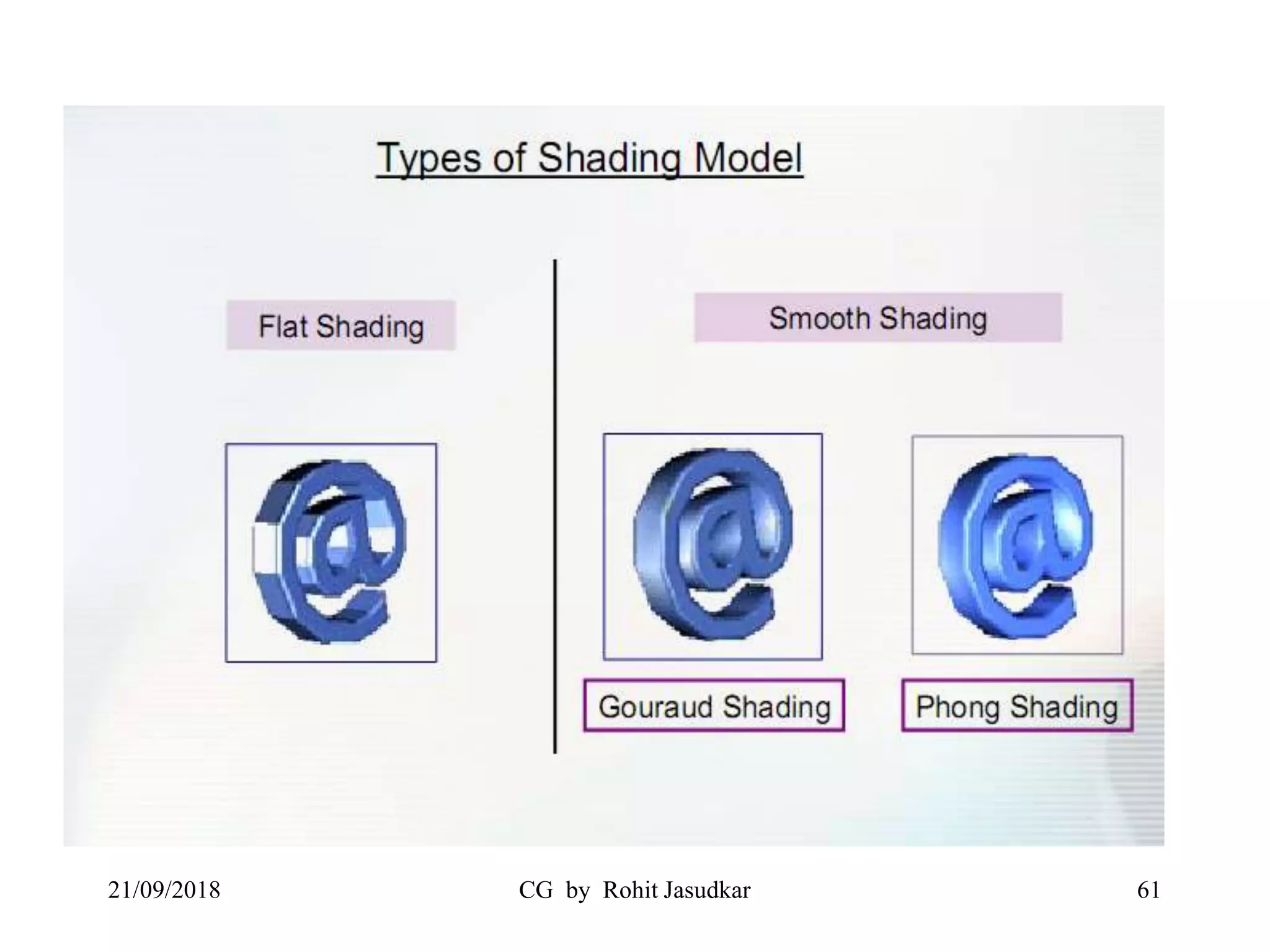
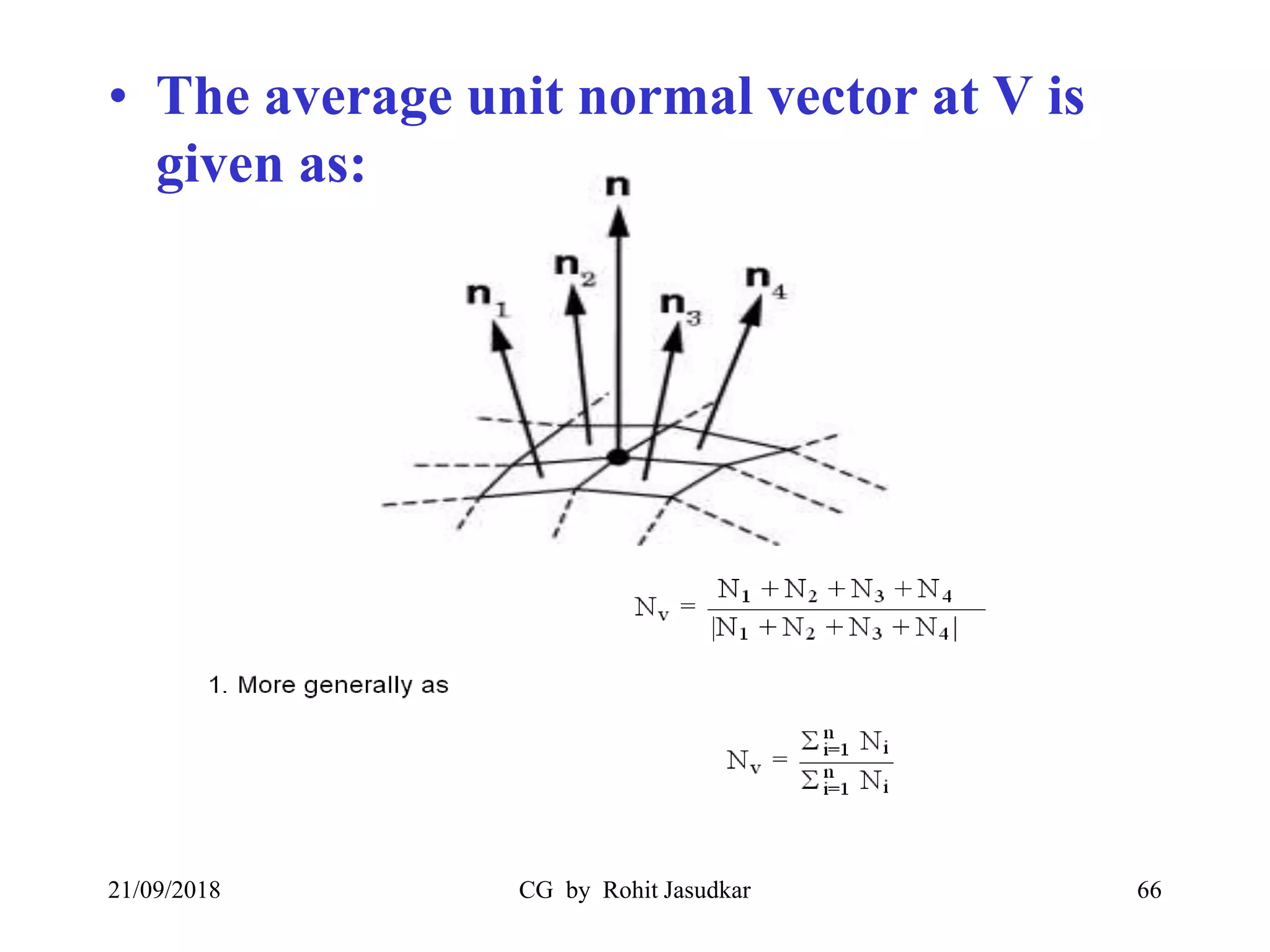
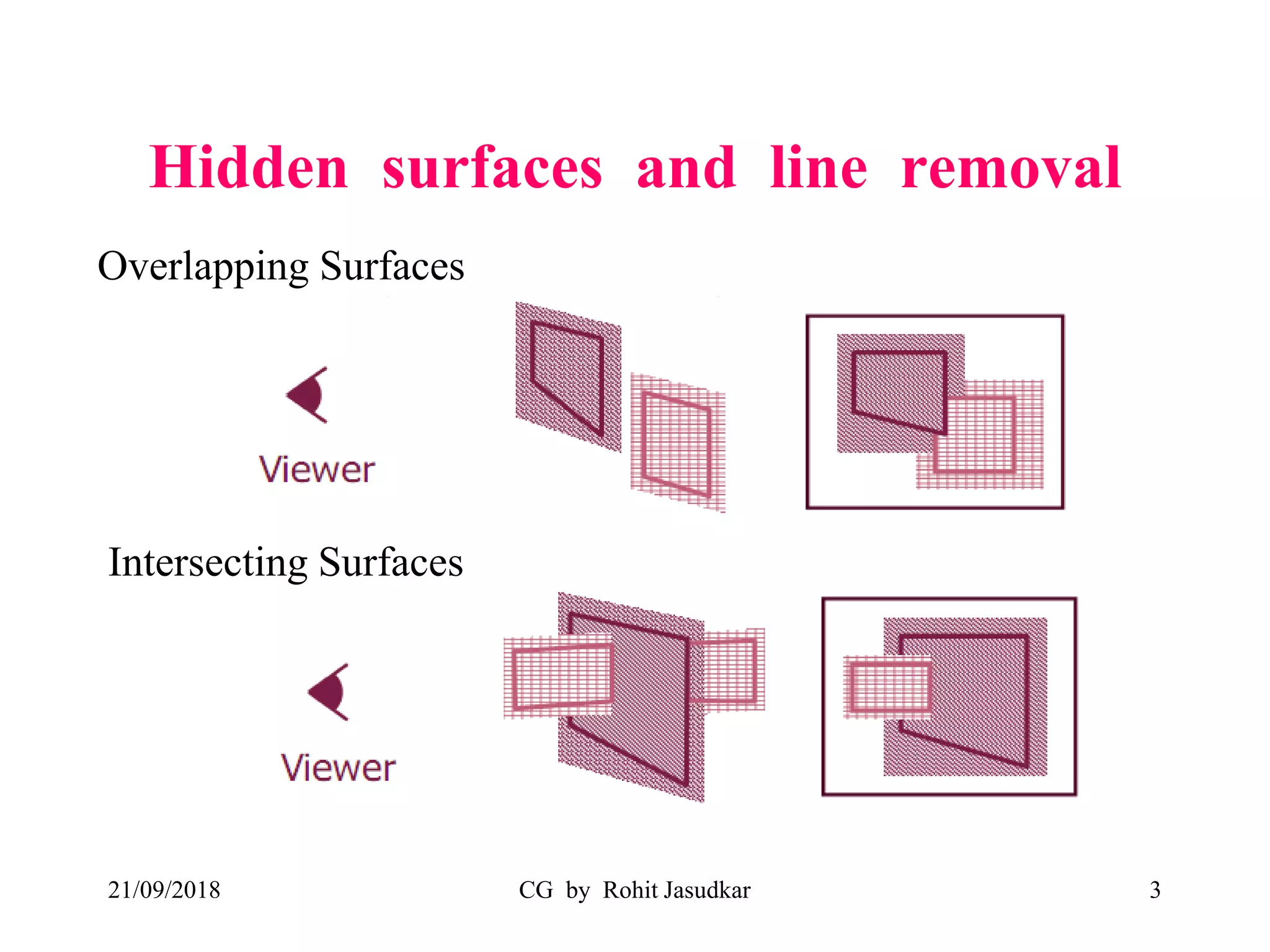
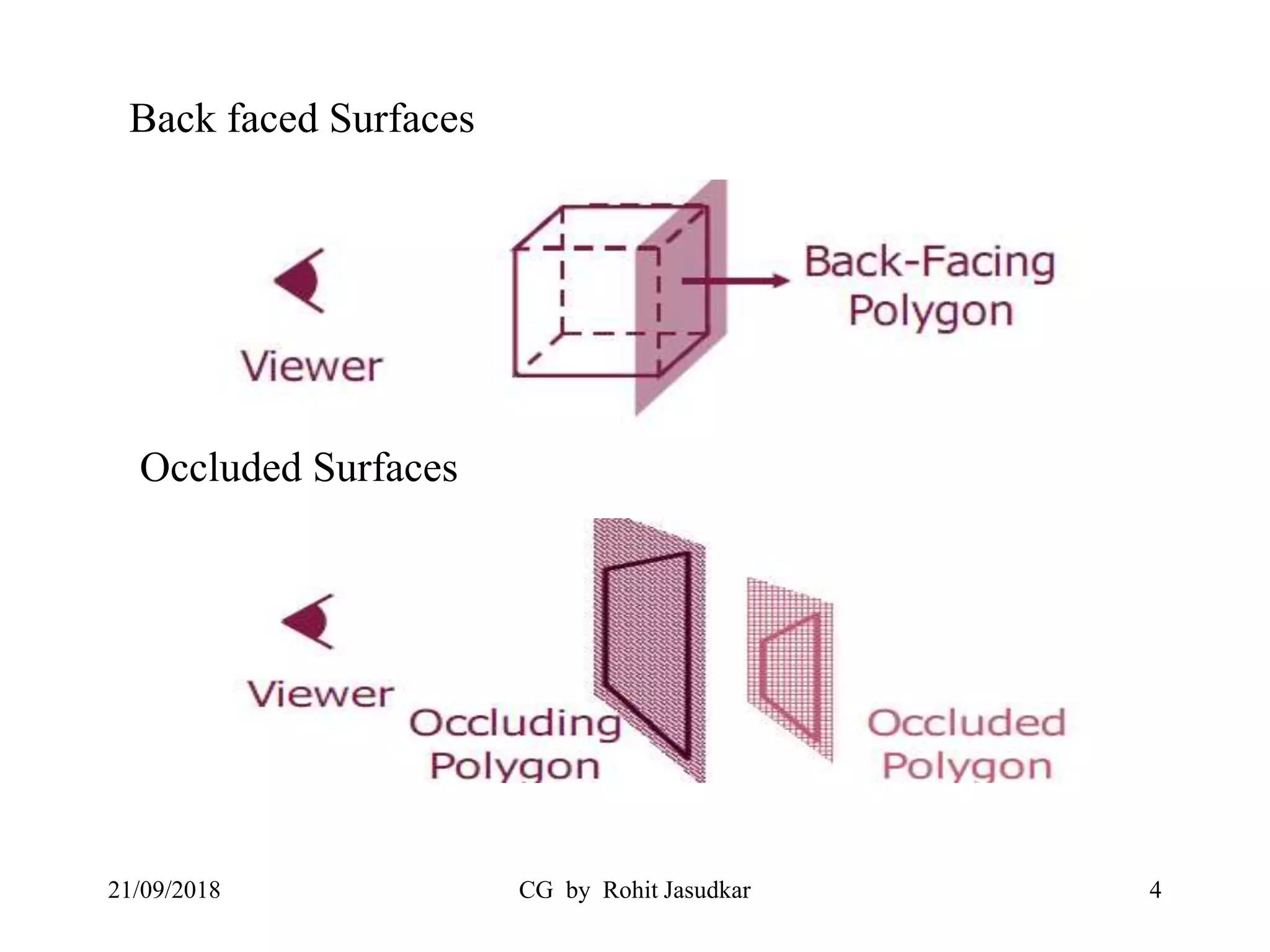
The document covers various methods in computer graphics focusing on hidden surfaces and line removal, including the z-buffer algorithm, Warnock's algorithm, and painter's algorithm. It also discusses curves and surfaces, highlighting Bezier and B-spline curves, followed by surface rendering methods like flat shading, Gouraud shading, and Phong shading. Each topic elaborates on techniques, advantages, and implementation strategies for creating realistic images in 3D graphics.








![• Two buffers are used
– Frame Buffer (Store Background intensity
or Shades)
– Depth Buffer (Store depth (Z) value of every
visible pixel in image space)
• The z-coordinates (depth values) are
usually normalized to the range [0,1]
21/09/2018 CG by Rohit Jasudkar 12](https://image.slidesharecdn.com/final-181119193646/75/Computer-Graphics-Hidden-surfaces-and-line-removal-Curves-and-surfaces-Surface-Rendering-Methods-12-2048.jpg)