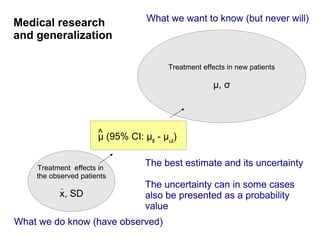
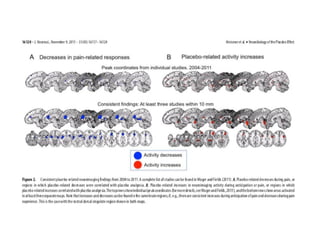
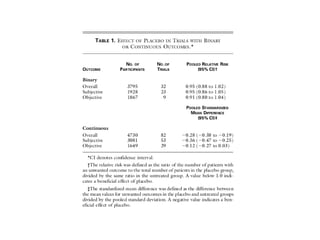
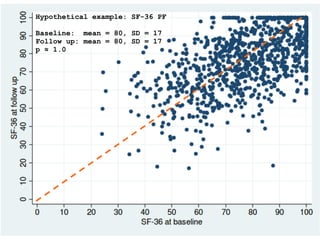
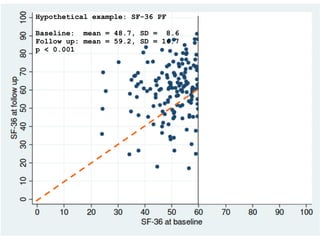
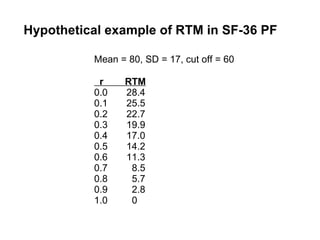
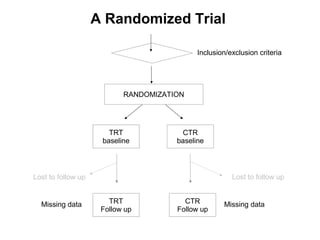
The document discusses the limitations of medical research, particularly focusing on statistical significance, the placebo effect, and regression to the mean. It highlights how the uncertainty in generalizing findings is often underestimated, and emphasizes the importance of critically evaluating the effects and methodologies used in clinical trials, including handling of missing data. Ultimately, it suggests that the evidence for the clinical effects of placebos is minimal and advises caution in their use outside controlled trials.

1. The SPSS-effect
on medical research
Jonas Ranstam

2. Generalization
Medical research studies are typically performed for
the benefit of other subjects than the participants.

3. Medical research What we want to know (but never will)
and generalization
Treatment effects in new patients
μ, σ
^ (95% CI: μ - μ )
μ ll ul
Treatment effects in
The best estimate and its uncertainty
the observed patients
The uncertainty can in some cases
x, SD also be presented as a probability
value
What we do know (have observed)

4. Medical research
in practice
p < 0.05 or ns
Some weird stuff that no one
Treatment effects in
the observed patients understands but is necessary
for getting manuscripts
x, SD accepted
What we do know (have observed)

5. Statistical significance and
Medical research insignificance is typically
in practice described as a property of the
sample, not the population:
SD, SEM and 95%Ci are all “there was a significant
believed to describe the difference”.
variability of observed data.
The presented conclusions are
This is the SPSS-effect on usually a summary of what has
medical research. been observed in the sample.
p < 0.05 or ns
Little (if anything) is mentioned
Treatment effects in
the observed patients
about the uncertainty in the
generalization of the findings.
x, SD
Many (if not all) authors severely
underestimate the uncertainty of
What we do know (have observed) their findings.

6. Statistics is about much more than
statistical significance
Important phenomena are neglected
Examples:
- Regression-to-the-mean (RTM)
- Consequences of missing data

7. The placebo effect and
regression to the mean

8. The Placebo effect is a real phenomenon
In conclusion, we believe that investigating the formation of
behavioral and biological changes due to placebos deserves
future efforts, as the placebo effect is a “real” neurobiological
phenomenon that has important implications for clinical
neuroscience research and medical care.
Meissner K. et al. The Placebo Effect: Advances from Different
Methodological Approaches. J Neurosci 2011; 31:16117–16124

11. Problem
The vast majority of reports on placebos have estimated the
effect of placebo as the change from baseline in the placebo
group of a randomized trial after treatment.
The effect of placebo can thus not be distinguished from the
natural course of the disease, regression to the mean, and
the effects of other factors.

13. Systematic review of the placebo effect
114 trials - 8525 patients
We included studies if patients were assigned randomly to a
placebo group or an untreated group (often there was also a
third group that received active treatment).

16. Publication bias?
There was significant heterogeneity among the trials with
continuous outcomes (P<0.001). The magnitude of the
effect of placebo decreased with increasing sample size
(P=0.05), indicating a possible bias related to the effects
of small trials.

17. Conclusion
In conclusion, we found little evidence that placebos in
general have powerful clinical effects.
Placebos had no significant pooled effect on subjective or
objective binary or continuous objective outcomes.
We found significant effects of placebo on continuous
subjective outcomes and for the treatment of pain but
also bias related to larger effects in small trials.
The use of placebo outside the aegis of a controlled,
properly designed clinical trial cannot be recommended.

18. Regression to the mean (RTM)
When an extreme group is selected from a population based
on the measurement of a particular variable, and a second
measurement is taken for the same group, the second mean
will be closer to the population mean than the first
measurement.

19. RTM
Any measurement taken consists of two components: the
‘true’ value plus a random error component. It is the random
error component that contributes to RTM. If the value of the
random error component is large, then the magnitude of the
corresponding RTM effects are increased.

20. Hypothetical example: SF-36 PF
Baseline: mean = 80, SD = 17
Follow up: mean = 80, SD = 17
p ≈ 1.0

21. Hypothetical example: SF-36 PF
Baseline: mean = 48.7, SD = 8.6
Follow up: mean = 59.2, SD = 16.7
p < 0.001

22. RTM - Easy to quantify
(for Normally distributed endpoints)
Barnett AG, van der Pols JC, Dobson AJ. Regression to the mean: what it is and how to deal with it. Int J
Epidemiol 2005;34:215–220

23. Hypothetical example of RTM in SF-36 PF
Mean = 80, SD = 17, cut off = 60
r RTM
0.0 28.4
0.1 25.5
0.2 22.7
0.3 19.9
0.4 17.0
0.5 14.2
0.6 11.3
0.7 8.5
0.8 5.7
0.9 2.8
1.0 0

24. RTM
Evaluation of a single groups’ development
over time should be avoided, or at least
include a comparison with the expected
RTM effect.

25. Examples
Diagnostic tests
New treatments
Public health efforts
Health care management
Clinical audits

26. Hospital comparisons
If one were a policy maker alert to the possibilities of using
RTM to ‘prove’ an initiative, one might target hospitals at
the bottom of the league table with an initiative, extra
resources, for example. RTM, combined with a floor effect,
will ensure that such a policy can be ‘proven’ to work.
Morton V, Torgerson DJ. Regression to the mean:
treatment effect without the intervention. J Eval Clin Pract
2005;11:59-65.

27. The consequences of
missing values

28. A Randomized Trial
Inclusion/exclusion criteria
RANDOMIZATION
TRT CTR
TRT
baseline baseline
Lost to follow up Lost to follow up
Missing data TRT CTR Missing data
Follow up Follow up

29. Study populations
Intention-to-treat (ITT)
Patients are analyzed according to randomization outcome
irrespective of received treatment or any protocol violation.
Per-protocol (PP)
The subgroup of the ITT population that has been treated
according to the study protocol.
Full Analysis Set (FAS)
The ITT population with exclusion of missing data.

30. Consequence of missing data
Precision
- reduced power
- variability
Validity
- comparability of treatment groups
- the representativity of the results

31. Missing data definitions
Missing outcome values
MCAR (missing completely at random)
- independent of both observed and unobserved variables.
MAR (missing at random)
- depend only on observed variables.
MNAR (missing not at random)
- depend on unobserved variables.

32. Handling of missing data
1. Complete case analysis (violates the ITT principle, not FAS)
2. Single imputation methods, e.g. LOCF, (biased p-values)
3. Multiple imputation, MI, (requires MCAR or MAR)
4. Mixed models, GEE (requires MCAR or MAR)

33. Sensitivity analysis
- Compare FAS results with Complete Case analysis results.
- Define missing values as failures.
- Worst case scenario analysis: Define missing values as
failures in TRT and successes in CTR.