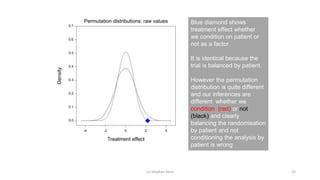
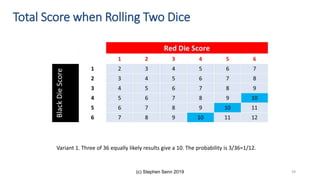
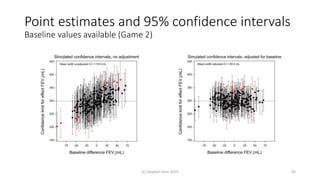
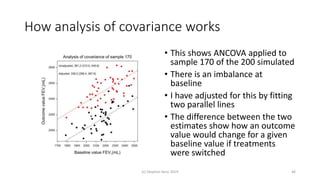
The document discusses the relationship between experiment design and data analysis, emphasizing that poorly designed studies can lead to misleading conclusions, regardless of the amount of data. It highlights the importance of careful experimental design while examining various statistical issues and challenges in clinical trials and observational studies. The author warns against over-reliance on big data claims, advocating for rigorous methodologies to ensure valid inferences.

1. To Infinity and Beyond
How ‘big’ are your data, really ?
Stephen Senn
Consultant Statistician
Edinburgh
(c) Stephen Senn 1
stephen@senns.uk

2. Acknowledgements
Many thanks for the invitation
This work is partly supported by the European Union’s 7th Framework
Programme for research, technological development and
demonstration under grant agreement no. 602552. “IDEAL”
(c) Stephen Senn 2(c) Stephen Senn 2

3. Outline
Part I (Not so technical and shorter)
• The roots of modern statistics
• Small data
• Careful design of experiments
• Some examples of problems with
judging causality from associations
in the health care field
• Two different objectives of clinical
trials
Part II (More technical and longer)
• Design
• The Rothamsted (Genstat)
approach
• Some statistical issues
• Conclusion
(c) Stephen Senn 3

4. Basic Thesis
• We know that there is a close and fundamental relationship between
how experiments are designed and how they should be analysed
• This should make us worry whenever we have to analyse data that
are not from a carefully designed study, however big that study may
be
• We should be sceptical of many of the claims we hear for the power
of ‘big data’
(c) Stephen Senn 4

5. Part I
Less technical matter to do with history of statistics and basic ‘philosophical’
considerations
(c) Stephen Senn 5

6. (c) Stephen Senn 6
John Nelder & Michael Healy

7. (c) Stephen Senn 7
William Sealy Gosset
1876-1937
• Born Canterbury 1876
• Educated Winchester and Oxford
• First in mathematical moderations 1897
and first in degree in Chemistry 1899
• Starts with Guinness in 1899 in Dublin
• Autumn 1906-spring 1907 with Karl
Pearson at UCL
• 1908 publishes ‘The probable error of a
mean’
• First method available to judge
‘significance’ in small samples

8. (c) Stephen Senn 8
Ronald Aylmer Fisher
1890-1962
• Most influential statistician ever
• Also major figure in evolutionary
biology
• Educated Harrow and Cambridge
• Statistician at Rothamsted agricultural
station 1919-1933
• Developed theory of small sample
inference and many modern concepts
• Likelihood, variance, sufficiency, ANOVA
• Developed theory of experimental
design
• Blocking, Randomisation, Replication,

9. Small data challenges
Situation Problem Solution
Sample size small Too few data to estimate variance
adequately
Develop small sample test
(Student)
Experimental material not
homogenous
Dealing with variability Blocking and randomisation
(Fisher)
Limited time (1) How to study more than one thing Complex treatment structure
factorial experiments (Fisher, Yates)
Limited time (2) How to study very many factors Fractional factorials. (Yates)
Experimental material varies at
different levels
Some treatments can be varied at
lowest level but not all
General balance approach to
analysis (Nelder)
(c) Stephen Senn 9

10. Characteristics of development of statistics in
the first half of the 20th century
• Numerical work was arduous and long
• Human computers
• Desk calculators
• Careful thought as to how to perform a calculation paid dividends
• Much development of inferential theory for small samples
• Design of experiments became a new subject in its own right developed by
statisticians
• Orthogonality
• Made calculation easier (eg decomposition of variance terms in ANOVA)
• Increased efficiency
• Randomisation
• “Guaranteed” properties of statistical analysis
• Dealt with hidden confounders
• Factorial experimentation
• Efficient way to study multiple influences
(c) Stephen Senn 10

11. TARGET study
• Trial of more than 18,000
patients in osteoarthritis over
one year or more
• Two sub-studies
• Lumiracoxib v ibuprofen
• Lumiracoxib v naproxen
• Stratified by aspirin use or not
• Has some features of a
randomised trial but also
some of a non-randomised
study
(c) Stephen Senn 11

12. Data Filtering Some Examples
Finding
• Oscar winners lived longer than actors who
didn’t win an Oscar
• A 20 year follow-up study of women in an
English village found higher survival amongst
smokers than non-smokers
• Transplant receivers on highest doses of
cyclosporine had higher probability of graft
rejection than on lower doses
• Left-handers observed to die younger on
average than right-handers
• Obese infarct survivors have better prognosis
than non-obese
Possible Explanation
• The longer you live the greater your
chance of winning
• The smokers were from more recent
generations. They were much younger
than non-smokers
• The anticipated transplant rejection was
the cause of the dose being increased
• In an earlier era left-handers were forced
to become right-handers
• There are two kinds of infarct: very
serious which is independent of weight
and less serious linked to obesity.
(c) Stephen Senn 12

13. Morals
• What you don’t see can be important
• Where you have not been able to run trials, biases
can be very important
• TARGET study provides a strong warning
• Observational studies show that alternative explanations
are possible
• For some purposes just piling on data does not really
help
• What helps are
• Careful design
• Thinking!
(c) Stephen Senn 13

14. We tend to believe “the truth is in
there”, but sometimes it isn’t and
the danger is we will find it
anyway
(c) Stephen Senn 14

15. Causal versus predictive inference
• Clinical trials can be used to try and answer a number of very
different questions
• Two examples are
• Did the treatment have an effect in these patients?
• A causal purpose
• What will the effect be in future patients?
• A predictive purpose
• Unfortunately, in practice, an answer is produced without stating
what the question was
• Given certain assumptions these questions can be answered using the
same analysis but the assumptions are strong and rarely stated
(c) Stephen Senn 15

16. Two models
Predictive
• The population is taken to be ‘patients in
general’
• Of course this really means future
patients
• They are the ones to whom the
treatment will be applied
• We treat the patients in the trial as an
appropriate selection from this population
• This does not require them to be typical
but it does require additivity of the
treatment effect
Causal
• We take the patients as fixed
• We want to know what the effect was for
them
• Unfortunately there are missing
counterfactuals
• What would have happened to control
patients given intervention and vice-versa
• The population is the population of all
possible allocations to the patients studied
(c) Stephen Senn 16

17. Coverage probabilities for two questions
Predictive Causal
(c) Stephen Senn 17
60 trials

18. Part II
Technical matters to do with design and inference
(c) Stephen Senn 18

19. Trial in asthma
Basic situation
• Two beta-agonists compared
• Zephyr(Z) and Mistral(M)
• Block structure has several levels
• Different designs will be investigated
• Cluster
• Parallel group
• Cross-over Trial
• Each design will be blocked at a different
level
• NB Each design will collect
6 x 4 x 2 x 7 = 336 measurements of Forced
Expiratory Volume in one second (FEV1)
Block structure
Level Number
within higher
level
Total
Number
Centre 6 6
Patient 4 24
Episodes 2 48
Measurements 7 336
(c) Stephen Senn 19

20. Block structure
• Patients are nested with centres
• Episodes are nested within patients
• Measurements are nested within
episodes
• Centres/Patients/Episodes/Measurements
(c) Stephen Senn 20
Measurements not shown

21. Possible designs
• Cluster randomised
• In each centre all the patients either receive Zephyr (Z) or Mistral (M) in both
episodes
• Three centres are chosen at random to receive Z and three to receive M
• Parallel group trial
• In each centre half the patients receive Z and half M in both episodes
• Two patients per centre are randomly chosen to receive Z and two to receive
M
• Cross-over trial
• For each patient the patient receives M in one episode and Z in another
• The order of allocation, ZM or MZ is random
(c) Stephen Senn 21

22. (c) Stephen Senn 22

23. (c) Stephen Senn 23

24. (c) Stephen Senn 24

25. Null (skeleton) analysis of variance with Genstat ®
Code Output
(c) Stephen Senn 25
BLOCKSTRUCTURE Centre/Patient/Episode/Measurement
ANOVA

26. Full (skeleton) analysis of variance with Genstat ®
Additional Code Output
(c) Stephen Senn 26
TREATMENTSTRUCTURE Design[]
ANOVA
(Here Design[] is a pointer with values corresponding
to each of the three designs.)

27. The bottom line
• The approach recognises that things vary
• Centres, patients episodes
• It does not require everything to be balanced
• Things that can be eliminated will be eliminated by design
• Cross-over trial eliminates patients and centres
• Parallel group trial eliminates centres
• Cluster randomised eliminates none of these
• The measure of uncertainty produced by the analysis will reflected what
cannot be eliminated
• This requires matching the analysis to the design
• Note that Genstat® deals with this formally and automatically. Other
packages do not.
(c) Stephen Senn 27

28. (c) Stephen Senn 28
To call in the statistician after
the experiment is done may be
no more than asking him to
perform a post-mortem
examination: he may be able
to say what the experiment
died of
RA Fisher

29. A genuine example ( a real trial)
Hills and Armitage 1979
• A cross-over trial of enuresis
• Patients randomised to one of two sequences
• Active treatment in period 1 followed by placebo in period 2
• Placebo in period 1 followed by active treatment in period 2
• Treatment periods were 14 days long
• Number of dry nights measured
(c) Stephen Senn 29

30. Important points to note
• Because every patient acts as his own control all patient level
covariates (of which there could be thousands and thousands) are
perfectly balanced
• Differences in these covariates can have no effect on the difference
between results under treatment and the results under placebo
• However, period level covariates (changes within the lives of patients)
could have an effect
• My normal practice is to fit a period effect as well as patients effects,
however, I shall omit doing so to simplify
• The parametric analysis then reduces to what is sometimes called a
matched pairs t-test
(c) Stephen Senn 30

31. Cross-over trial in
Enuresis
Two treatment periods of
14 days each
1. Hills, M, Armitage, P. The two-period
cross-over clinical trial, British Journal of Clinical
Pharmacology 1979; 8: 7-20.
(c) Stephen Senn 31

32. Two Parametric Approaches
Not fitting patient effect
Estimate s.e. t(56) t pr.
2.172 0.964 2.25 0.0282
Fitting patient effect
Estimate s.e. t(28) t pr
.
2.172 0.616 3.53 0.00147
(c) Stephen Senn
Note that ignoring the patient effect, the P-value is less impressive and the standard
error is larger
The method posts higher uncertainty because unlike the within-patient analysis it make
no assumption that the patient level covariates are balanced.
Of course, in this case, since we know the patient level covariates are balanced, this
analysis is wrong
32

33. Blue diamond shows
treatment effect whether
we condition on patient or
not as a factor.
It is identical because the
trial is balanced by patient.
However the permutation
distribution is quite different
and our inferences are
different whether we
condition (red) or not
(black) and clearly
balancing the randomisation
by patient and not
conditioning the analysis by
patient is wrong
(c) Stephen Senn 33

34. The two permutation* distributions summarised
Summary statistics for Permuted difference no
blocking
Number of observations = 10000
• Mean = -0.00319
• Median = -0.0345
• Minimum = -3.621
• Maximum = 3.690
• Lower quartile = -0.655
• Upper quartile = 0.655
Standard deviation = 0.993
P-value for observed difference 0.0344
(Parametric P-value 0.0282)
*Strictly speaking, these are randomisation
distributions
Summary statistics for Permuted difference
blocking
Number of observations = 10000
• Mean = -0.00339
• Median = 0.0345
• Minimum = -2.793
• Maximum = 2.517
• Lower quartile = -0.517
• Upper quartile = 0.517
P-value for observed difference 0.001
(Parametric P-value 0.00147)
(c) Stephen Senn 34

35. What happens if you balance but don’t
condition?
Approach Variance of estimated
treatment effect over all
randomisations*
Mean of estimated
variance of treatment
effect over all
randomisations*
Completely randomised
Analysed as such
0.987 0.996
Randomised within-patient
Analysed as such
0.534 0.529
Randomised within-patient
Analysed as completely
randomised
0.534 1.005
*Based on 10000 random permutations
(c) Stephen Senn 35
That is to say, permute values respecting the fact that they come from a cross-over but analyse them as if
they came from a parallel group trial

36. 36
The difference between
mathematical and applied
statistics is that the former is full
of lemmas whereas the latter is
full of dilemmas
(c) Stephen Senn

37. The Shocking Truth
• The validity of conventional analysis of randomised trials does not
depend on covariate balance
• It is valid because they are not perfectly balanced
• An allowance is already made for things being unbalanced
• If they were balanced the standard analysis would be wrong
• Like an insurance broker forbidding you to travel abroad in the policy but
calculating your premiums on the assumption that you will
• This accounts for unobserved covariates. What happens when they
are observed?
(c) Stephen Senn 2019 37

38. (c) Stephen Senn 2019
• Two dice are rolled
– Red die
– Black die
• You have to call correctly the probability of a total score of 10
• Three variants
– Game 1 You call the probability and the dice are rolled
together
– Game 2 the red die is rolled first, you are shown the score
and then must call the probability
– Game 3 the red die is rolled first, you are not shown the
score and then must call the probability
Game of Chance
38

39. (c) Stephen Senn 2019
Total Score when Rolling Two Dice
Variant 1. Three of 36 equally likely results give a 10. The probability is 3/36=1/12.
39

40. (c) Stephen Senn 2019
Variant 2: If the red die score is 1,2 or 3, the probability of a total of10 is 0.
If the red die score is 4,5 or 6, the probability of a total of10 is 1/6.
Variant 3: The probability = (½ x 0) + (½ x 1/6) = 1/12
Total Score when Rolling Two Dice
40

41. The morals
Dice games
• You can’t treat game 2 like game 1
• You must condition on the information
received
• You must use the actual data from the red die
• You can treat game 3 like game 1
• You can use the distribution in probability
that the red die has
Inference in general
• You can’t use the random behavior of
a system to justify ignoring
information that arises from the
system
• That would be to treat game 2 like game 1
• You can use the random behavior of
the system to justify ignoring that
which has not been seen
• You are entitled to treat game 3 like game 1
(c) Stephen Senn 2019 41

42. What does the Rothamsted approach do?
• Matches the allocation procedure to the analysis. You can either
regard this as meaning
• The randomisation you carried out guides the analysis
• The analysis you intend guides the randomisation
• Or both
• Either way, the idea is to avoid inconsistency
• Regarding something as being very important at the allocation stage but not
at the analysis stage is inconsistent
• Permits you not only to take account of things seen but also to make
an appropriate allowance for things unseen
• Die analogy is that it makes sure that the game is a fair one
(c) Stephen Senn 42

43. A simulating example
• I am going to simulate 200 clinical trials
• Trials are of a bronchodilator against placebo.
• Simple randomisation of 50 patients to each arm
• I shall have values at outcome and values at baseline
• Forced expiratory volume in one second (FEV1) in mL
• Parameter settings
• True mean under placebo 2200 mL
• Under bronchodilator 2500 mL
• Treatment effect is 300 mL
• SD at outcome and baseline is 150 mL
• Correlation is 0.7
(c) Stephen Senn 2019 43

44. Point estimates and confidence intervals
Baseline values not available (like game 1)
(c) Stephen Senn 2019 44

45. Point estimates and 95% confidence intervals
Baseline values available (Game 2)
(c) Stephen Senn 2019 45

46. How analysis of covariance works
• This shows ANCOVA applied to
sample 170 of the 200 simulated
• There is an imbalance at
baseline
• I have adjusted for this by fitting
two parallel lines
• The difference between the two
estimates show how an outcome
value would change for a given
baseline value if treatments
were switched
(c) Stephen Senn 2019 46

47. Lessons for big data
• We tend to treat observational data-sets as if they were badly
randomised parallel group trials but cluster-randomised trials might
be a better analogy
• True standard errors may be much bigger than estimated ones
• See Cox, Kartsonaki & Keogh (2018) and Xiao-Li Meng (2018)
• Design matters
• Beware of dreams in which mathematics triumphs over biology
• You can be rich in data but poor in information
(c) Stephen Senn 2019 47

48. A big data analyst is an expert at reaching
misleading conclusions with huge data sets,
whereas a statistician can do the same with
small ones
(c) Stephen Senn 48

49. References
(c) Stephen Senn 49
D. R. Cox, C. Kartsonaki and R. H. Keogh (2018) Big data: Some statistical issues. Stat Probab Lett, 111-
115.
X.-L. Meng (2018) Statistical paradises and paradoxes in big data (I): Law of large populations, big
data paradox, and the 2016 US presidential election. The Annals of Applied Statistics, 685-726.
S. J. Senn (2013) Seven myths of randomisation in clinical trials. Statistics in Medicine, 1439-1450.
S. Senn (2013) A Brief Note Regarding Randomization. Perspectives in biology and medicine, 452-453.
S. J. Senn (2019) The well-adjusted statistician. Applied Clinical Trials, June 18.
https://www.appliedclinicaltrialsonline.com/view/well-adjusted-statistician-analysis-covariance-
explained
S. Senn (2019) John Ashworth Nelder. 8 October 1924—7 August 2010: The Royal Society Publishing.
A number of blogs on my blog site are also relevant: http://www.senns.uk/Blogs.html