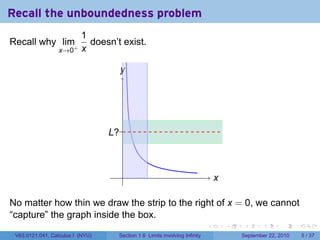
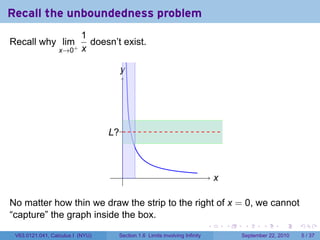
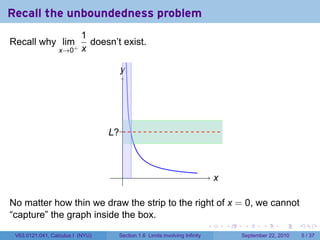
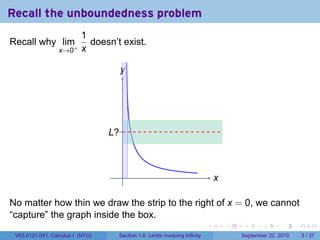
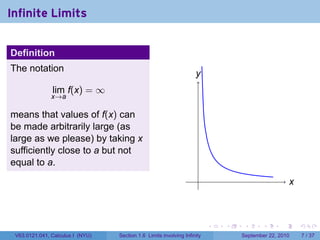
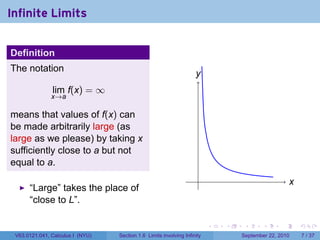
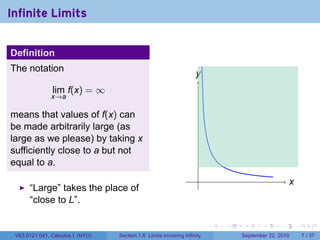
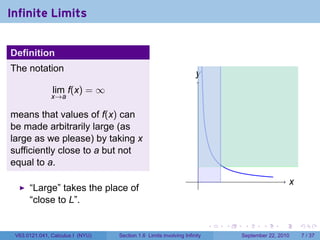
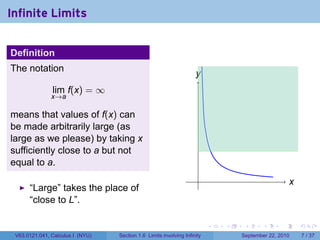
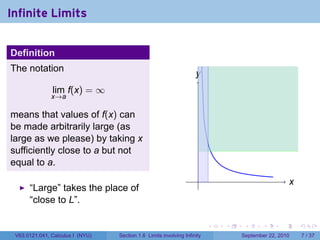
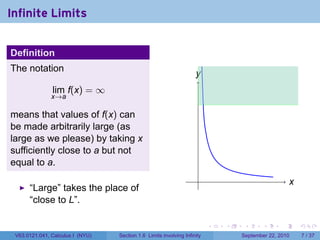
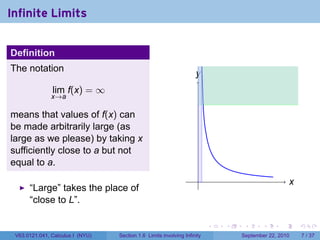
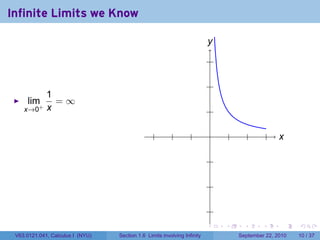
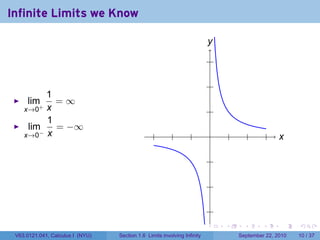
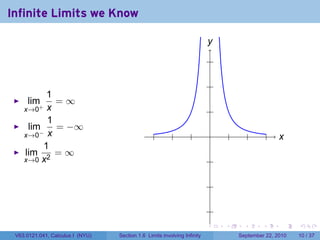
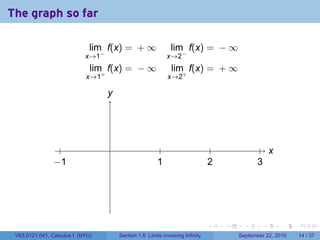
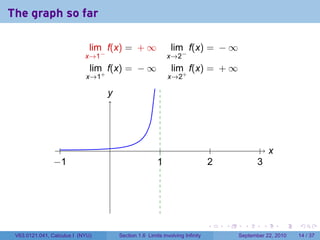
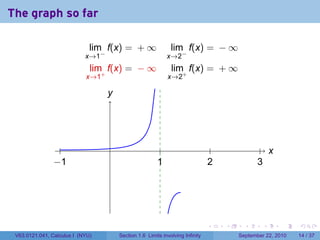
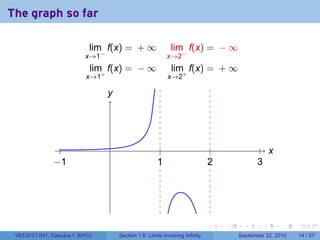
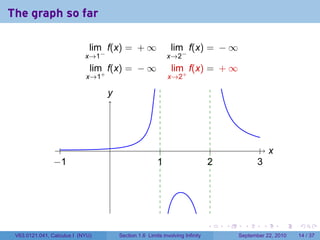
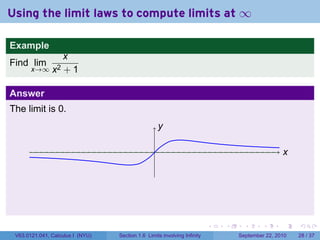
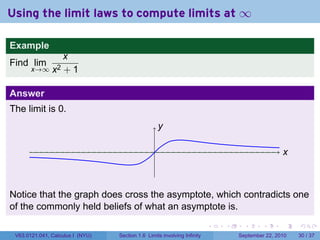
This document is from a Calculus I course at New York University and covers limits involving infinity. It discusses definitions of limits approaching positive or negative infinity. Examples are provided of functions with infinite limits, such as 1/x as x approaches 0. The document outlines techniques for finding limits at points where a function is not continuous, such as using a number line to determine the signs of factors in a rational function's denominator.