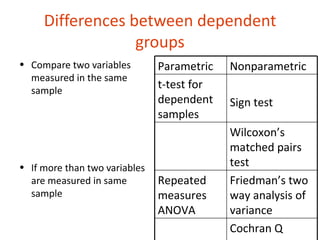
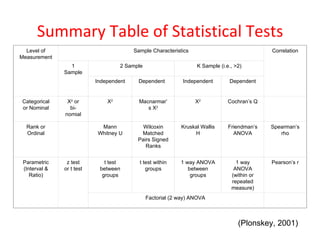
This document discusses parametric and nonparametric statistics, when each should be used, and their relative power. Parametric tests make assumptions about the population that may not always be justified, while nonparametric tests do not rely on these assumptions. Some key points: 1. Parametric tests assume normal distributions and equal variances, while nonparametric tests do not require these assumptions and can be used on small sample sizes or ordinal data. 2. There are nonparametric equivalents to most common parametric tests for comparing groups (independent or dependent samples) or relationships between variables. 3. Advantages of nonparametric tests are they provide exact probabilities regardless of the population distribution and can

1. Parametric versus Nonparametric
Statistics – When to use them and
which is more powerful?
By Rama Krishna Kompella

2. Parametric Assumptions
• The observations must be independent
• The observations must be drawn from
normally distributed populations
• These populations must have the same
variances
• Observations are independent
• Variable under study has underlying
continuity

3. Nonparametric Alternative
• The parametric assumptions cannot be
justified: normal distribution, equal variances,
etc.
• The data as gathered are measured on
nominal or ordinal data
• Sample size is small.
3

4. Nonparametric Methods
• There is at least one nonparametric test
equivalent to a parametric test
• These tests fall into several categories
1. Tests of differences between groups
(independent samples)
2. Tests of differences between variables
(dependent samples)
3. Tests of relationships between variables

5. Differences between independent
groups
• Two samples – compare Parametric Nonparametric
mean value for some
variable of interest t-test for Wald-Wolfowitz
independent runs test
samples
Mann-Whitney U
test
Kolmogorov-
Smirnov two
sample test

6. Differences between independent
groups
Parametric Nonparametric
• Multiple groups Analysis of Kruskal-Wallis
variance analysis of ranks
(ANOVA/
MANOVA)
Median test

7. Differences between dependent
groups
• Compare two variables Parametric Nonparametric
measured in the same
sample
t-test for
dependent Sign test
samples
Wilcoxon’s
matched pairs
• If more than two variables test
are measured in same Repeated Friedman’s two
sample measures way analysis of
ANOVA variance
Cochran Q

8. Relationships between variables
Parametric Nonparametric
Correlation Spearman R
coefficient
Kendall Tau
Coefficient Gamma
Chi square
• Two variables
Phi coefficient
of interest are
Fisher exact test
categorical
Kendall coefficient of
concordance

9. Summary Table of Statistical Tests
Level of Sample Characteristics Correlation
Measurement
1 2 Sample K Sample (i.e., >2)
Sample
Independent Dependent Independent Dependent
Categorical Χ2 or Χ2 Macnarmar’ Χ2 Cochran’s Q
or Nominal bi- s Χ2
nomial
Rank or Mann Wilcoxin Kruskal Wallis Friendman’s Spearman’s
Ordinal Whitney U Matched H ANOVA rho
Pairs Signed
Ranks
Parametric z test t test t test within 1 way ANOVA 1 way Pearson’s r
(Interval & or t test between groups between ANOVA
Ratio) groups groups (within or
repeated
measure)
Factorial (2 way) ANOVA
(Plonskey, 2001)

10. Advantages of Nonparametric Tests
• Probability statements obtained from most
nonparametric statistics are exact
probabilities, regardless of the shape of the
population distribution from which the
random sample was drawn
• If sample sizes as small as N=6 are used, there
is no alternative to using a nonparametric test
Siegel, 1956

11. Advantages of Nonparametric Tests
• Treat samples made up of observations from several
different populations.
• Can treat data which are inherently in ranks as well
as data whose seemingly numerical scores have the
strength in ranks
• They are available to treat data which are
classificatory
• Easier to learn and apply than parametric tests
Siegel, 1956

12. Criticisms of Nonparametric
Procedures
• Losing precision/wasteful of data
• Low power
• False sense of security
• Lack of software
• Testing distributions only
• Higher-ordered interactions not dealt with

13. Questions?