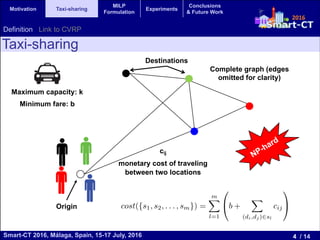
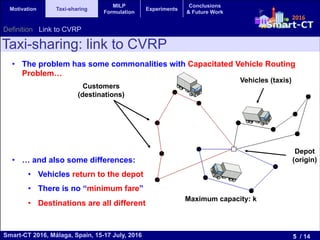
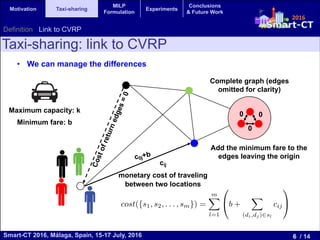
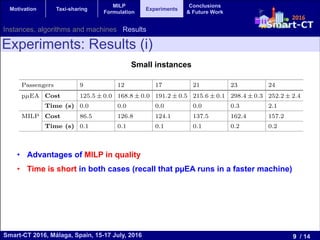
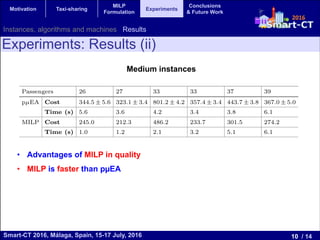
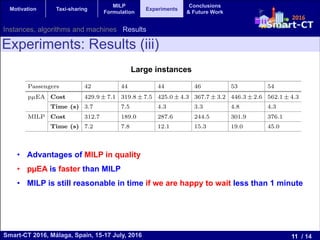
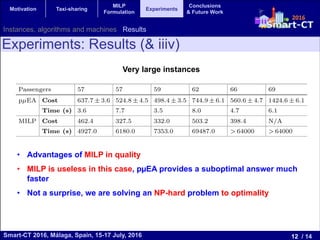
The document presents a mixed integer linear programming (MILP) formulation for solving the taxi sharing problem. The taxi sharing problem aims to optimize taxi routes by allowing passengers with similar pick-up and drop-off locations to share taxis. The formulation models the problem as sequences of passenger locations that represent taxi rides. Experiments on real-world taxi trip data show the MILP formulation finds lower cost solutions than a parallel evolutionary algorithm, especially on medium and large problem instances, demonstrating the benefits of the exact MILP approach.

1. 1 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Mixed Integer Linear Programming
Formulation for the Taxi Sharing Problem
Houssem E. Ben-Smida, Saoussen Krichen,
Francisco Chicano, Enrique Alba

2. 2 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Motivation
• One of the goals of Smart Cities is to increase efficiency in the use of
resources
• Translated to Smart Mobility, efficiency generate benefits both
economically and ecologically

3. 3 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Motivation
• Shared trips is a way to improve mobility resources
• Several people share the transport (public or private vehicle)
• Some proposals are:
• Lanes for cars with two or more passengers
• Campaigns to share the car to/from the workplace
• Applications to find travelign companions
• BlaBlaCar or Carma
• What about taxis?
• They rarely travel full
• Impact in pollution and economy of users
• Solution: Taxi-sharing

4. 4 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Taxi-sharing
Complete graph (edges
omitted for clarity)
cij
monetary cost of traveling
between two locations
Maximum capacity: k
Minimum fare: b
Mixed Integer Linear Programming Formulation
In the following we will present the mathematical formulation of the p
Let P = {p1, p2, ..., pn} be a set of n passengers that are in the same
d0. Let us denote with di the location where passenger pi wants to go
assume that the maximum capacity of the available taxis is k (usually 4
and let us denote with b the minimum fare to pay in each trip regard
distance traveled. The cost to travel from point di to dj will be given
matrix element cij of a cost matrix.
A solution to the problem is a set of m sequences of locations {s1, s2,
such that every destination di with i ≥ 1 appears exactly in one sequen
no more than one), and the origin d0 is the first location in all the se
Each sequence of locations represents a taxi ride, where the destination
sequence are visited in the order they appear. The length of each seq
will be k + 1 at most, since k is the maximum capacity of the taxis and
first location in all the sequences. The total cost of a solution is given b
cost({s1, s2, . . . , sm}) =
m
l=1
⎛
⎝b +
(di,dj )∈sl
cij
⎞
⎠ ,
where we use (di, dj) ∈ sl to iterate over all the pairs of destinations
AuthorProof
Origin
Destinations
Definition Link to CVRP

5. 5 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Taxi-sharing: link to CVRP
Definition Link to CVRP
• The problem has some commonalities with Capacitated Vehicle Routing
Problem…
• … and also some differences:
• Vehicles return to the depot
• There is no “minimum fare”
• Destinations are all different
Depot
(origin)
Vehicles (taxis)
Customers
(destinations)
Maximum capacity: k

6. 6 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Taxi-sharing: link to CVRP
Complete graph (edges
omitted for clarity)
cij
monetary cost of traveling
between two locations
Maximum capacity: k
Minimum fare: b
Mixed Integer Linear Programming Formulation
In the following we will present the mathematical formulation of the p
Let P = {p1, p2, ..., pn} be a set of n passengers that are in the same
d0. Let us denote with di the location where passenger pi wants to go
assume that the maximum capacity of the available taxis is k (usually 4
and let us denote with b the minimum fare to pay in each trip regard
distance traveled. The cost to travel from point di to dj will be given
matrix element cij of a cost matrix.
A solution to the problem is a set of m sequences of locations {s1, s2,
such that every destination di with i ≥ 1 appears exactly in one sequen
no more than one), and the origin d0 is the first location in all the se
Each sequence of locations represents a taxi ride, where the destination
sequence are visited in the order they appear. The length of each seq
will be k + 1 at most, since k is the maximum capacity of the taxis and
first location in all the sequences. The total cost of a solution is given b
cost({s1, s2, . . . , sm}) =
m
l=1
⎛
⎝b +
(di,dj )∈sl
cij
⎞
⎠ ,
where we use (di, dj) ∈ sl to iterate over all the pairs of destinations
AuthorProof
• We can manage the differences
Add the minimum fare to the
edges leaving the origin
0
0
0
Definition Link to CVRP

7. 7 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Mixed Integer Linear Programming
• Based on Kulkarni and Bhave’s formulation afor CVRP
• There is an error in that formulation that does not affect taxi-sharing
Mixed Integer Linear Programming Formu
yi − yj + nxij ≤ n − 1 for 1 ≤ i ̸= j ≤ n,
ui − uj + kxij ≤ k − 1 for 1 ≤ i ̸= j ≤ n,
xij = 0 or 1 for 0 ≤ i ̸= j ≤ n,
ui, yi ∈ R for 1 ≤ i ≤ n.
Constraints (3) and (4) ensure that each location is visited onl
straint (5) is designed to ensure that no subtours are formed and, th
that all routes must visit the origin. The yi variables are introdu
AuthorProof
if we find a way to deal with these three differences.
der to model the fact that taxis do not need to go back to the depot,
o the cost of return equals zero. This way, although the solutions will
osed of closed paths, there is no cost related to the final segment (that
k to the origin). The minimum fare can be added to the cost of the first
of any path. In particular, it can be added to all the edges that leave
n. Finally, all the passenger destinations can be considered as different.
f them are the same in a particular instance of the problem, we add a
edge between them. With these considerations, we can adapt the MILP
on of CVRP to Taxi Sharing.
ssume c0i is the cost from the origin to the location plus the minimum
the customers have to pay to the taxi. The values ci0 will be 0 as
d above. The Mixed Integer Linear Program formulation of the Taxi
problem is:
min
n
i=0
n
j=0
cijxij, (2)
o:
n
i=0
xij = 1 for 1 ≤ j ≤ n, (3)
n
j=0
xij = 1 for 1 ≤ i ≤ n, (4)
ment of any path. In particular, it can be added to all the edges that leave
origin. Finally, all the passenger destinations can be considered as different
ome of them are the same in a particular instance of the problem, we add a
o cost edge between them. With these considerations, we can adapt the MILP
mulation of CVRP to Taxi Sharing.
We assume c0i is the cost from the origin to the location plus the minimum
e that the customers have to pay to the taxi. The values ci0 will be 0 a
plained above. The Mixed Integer Linear Program formulation of the Tax
aring problem is:
min
n
i=0
n
j=0
cijxij, (2
bject to:
n
i=0
xij = 1 for 1 ≤ j ≤ n, (3
n
j=0
xij = 1 for 1 ≤ i ≤ n, (4
Visit each node
only once Avoid subtours
Taxi capacity constraint Domains of variables

8. 8 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Experiments
Instances, algorithms and machines Results
• Set of 24 real-like instances used by Massobrio et al. (2014)
• Generated with Taxi Query Generator based on trajectories of more than
10,000 taxis in Beijing, China
• Sizes: from 9 to 69 passengers
• IBM CPLEX 12.6.2 for Windows for solving the MILP formulation
• Intel Core i5-4210U at 1.7GHz, 8 GB and Windows 10
• Parallel micro evolutionary algorithm with 24 subpopulations, 15
solutions per subpopulation, and greedy initialization strategy
• Cluster with Dell Power Edge servers, Quad-core Xeon E5430 at
2.66 GHz, 8 GB
Instances
Algorithms and machines
Best conf.

9. 9 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Experiments: Results (i)
Small instances
difference between the cost obtained with pµEA and the MILP solver is large
enough to justify the MILP approach. There is an important benefit. In some
cases, the MILP solver reaches almost half of the cost of the pµEA solution
Table 1. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the small instances of the Taxi Sharing Problem. For
pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 9 12 17 21 23 24
pµEA Cost 125.5 ± 0.0 168.8 ± 0.0 191.2 ± 0.5 215.6 ± 0.1 298.4 ± 0.3 252.2 ± 2.4
Time (s) 0.0 0.0 0.0 0.0 0.3 2.1
MILP Cost 86.5 126.8 124.1 137.5 162.4 157.2
Time (s) 0.1 0.1 0.1 0.1 0.2 0.2
• Advantages of MILP in quality
• Time is short in both cases (recall that pµEA runs in a faster machine)
Instances, algorithms and machines Results

10. 10 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Experiments: Results (ii)
Medium instances
Mixed Integer Linear Programming Formulation 7
Table 2. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the medium instances of the Taxi Sharing Problem.
For pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 26 27 33 33 37 39
pµEA Cost 344.5 ± 5.6 323.1 ± 3.4 801.2 ± 4.2 357.4 ± 3.4 443.7 ± 3.8 367.0 ± 5.0
Time (s) 5.6 3.6 4.2 3.4 3.8 6.1
MILP Cost 245.0 212.3 486.2 233.7 301.5 274.2
Time (s) 1.0 1.2 2.1 3.2 5.1 6.1
Table 3. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the large instances of the Taxi Sharing Problem. For
pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 42 44 44 46 53 54
pµEA Cost 429.9 ± 7.1 319.8 ± 7.5 425.0 ± 4.3 367.7 ± 3.2 446.3 ± 2.6 562.1 ± 4.3
Time (s) 3.7 7.5 4.3 3.3 4.8 4.3
MILP Cost 312.7 189.0 287.6 244.5 301.9 376.1
Time (s) 7.2 7.8 12.1 15.3 19.0 45.0
• Advantages of MILP in quality
• MILP is faster than pµEA
Instances, algorithms and machines Results

11. 11 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Experiments: Results (iii)
Large instances
• Advantages of MILP in quality
• pµEA is faster than MILP
• MILP is still reasonable in time if we are happy to wait less than 1 minute
pµEA Cost 344.5 ± 5.6 323.1 ± 3.4 801.2 ± 4.2 357.4 ± 3.4 443.7 ± 3.8 367.0 ± 5.0
Time (s) 5.6 3.6 4.2 3.4 3.8 6.1
MILP Cost 245.0 212.3 486.2 233.7 301.5 274.2
Time (s) 1.0 1.2 2.1 3.2 5.1 6.1
Table 3. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the large instances of the Taxi Sharing Problem. For
pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 42 44 44 46 53 54
pµEA Cost 429.9 ± 7.1 319.8 ± 7.5 425.0 ± 4.3 367.7 ± 3.2 446.3 ± 2.6 562.1 ± 4.3
Time (s) 3.7 7.5 4.3 3.3 4.8 4.3
MILP Cost 312.7 189.0 287.6 244.5 301.9 376.1
Time (s) 7.2 7.8 12.1 15.3 19.0 45.0
Table 4. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the very large instances of the Taxi Sharing Problem.
For pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 57 57 59 62 66 69
pµEA Cost 637.7 ± 3.6 524.8 ± 4.5 498.4 ± 3.5 744.9 ± 6.1 560.6 ± 4.7 1424.6 ± 6.1
Time (s) 3.6 7.7 3.5 8.0 4.7 6.1
MILP Cost 462.4 327.5 332.0 503.2 398.4 N/A
Time (s) 4927.0 6180.0 7353.0 69487.0 > 64000 > 64000
Instances, algorithms and machines Results

12. 12 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Experiments: Results (& iiiv)
Very large instances
• Advantages of MILP in quality
• MILP is useless in this case, pµEA provides a suboptimal answer much
faster
• Not a surprise, we are solving an NP-hard problem to optimality
Time (s) 3.7 7.5 4.3 3.3 4.8 4.3
MILP Cost 312.7 189.0 287.6 244.5 301.9 376.1
Time (s) 7.2 7.8 12.1 15.3 19.0 45.0
Table 4. Comparison between the MILP solver and pµEA with 24 subpopulations and
greedy initialization strategy for the very large instances of the Taxi Sharing Problem.
For pµEA, the average cost and standard deviation of 20 independent runs is reported.
Passengers 57 57 59 62 66 69
pµEA Cost 637.7 ± 3.6 524.8 ± 4.5 498.4 ± 3.5 744.9 ± 6.1 560.6 ± 4.7 1424.6 ± 6.1
Time (s) 3.6 7.7 3.5 8.0 4.7 6.1
MILP Cost 462.4 327.5 332.0 503.2 398.4 N/A
Time (s) 4927.0 6180.0 7353.0 69487.0 > 64000 > 64000
(see solution with n = 23 in Table 1). This observation is generalized, and it
does not seem to change with the number of passengers of the instances.
Regarding the execution time of the MILP solver and pµEA, we have to be
careful with the conclusions, since both algorithms are run in different machines,
with different cores. Although an accurate comparison is not possible here, we
can take some conclusions just seeing the order of magnitude of the runtime.
As we could expect both approaches require, in general, more time as the
Instances, algorithms and machines Results

13. 13 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Motivation Taxi-sharing
MILP
Formulation
Experiments
Conclusions
& Future Work
Conclusions and Future Work
Conclusions & Future Work
• Solving the MILP formulation we get optimal results in short
time for instances with up to 45 passengers (large instances)
• More than 45 passengers requires a different approach to
have an answer in a few seconds
• pµEA works well in these very large instances
Conclusions
• Combine exact and heuristic methods: matheuristics
• Extend the formulation to include more realistic scenarios:
real-time traffic, passengers’ time constraints, etc.
Future Work

14. 14 / 14Smart-CT 2016, Málaga, Spain, 15-17 July, 2016
Acknowledgements
Mixed Integer Linear Programming
Formulation for the Taxi Sharing Problem
Thanks to Renzo Massobrio, Gabriel
Fagúndez and Sergio Nesmachnow