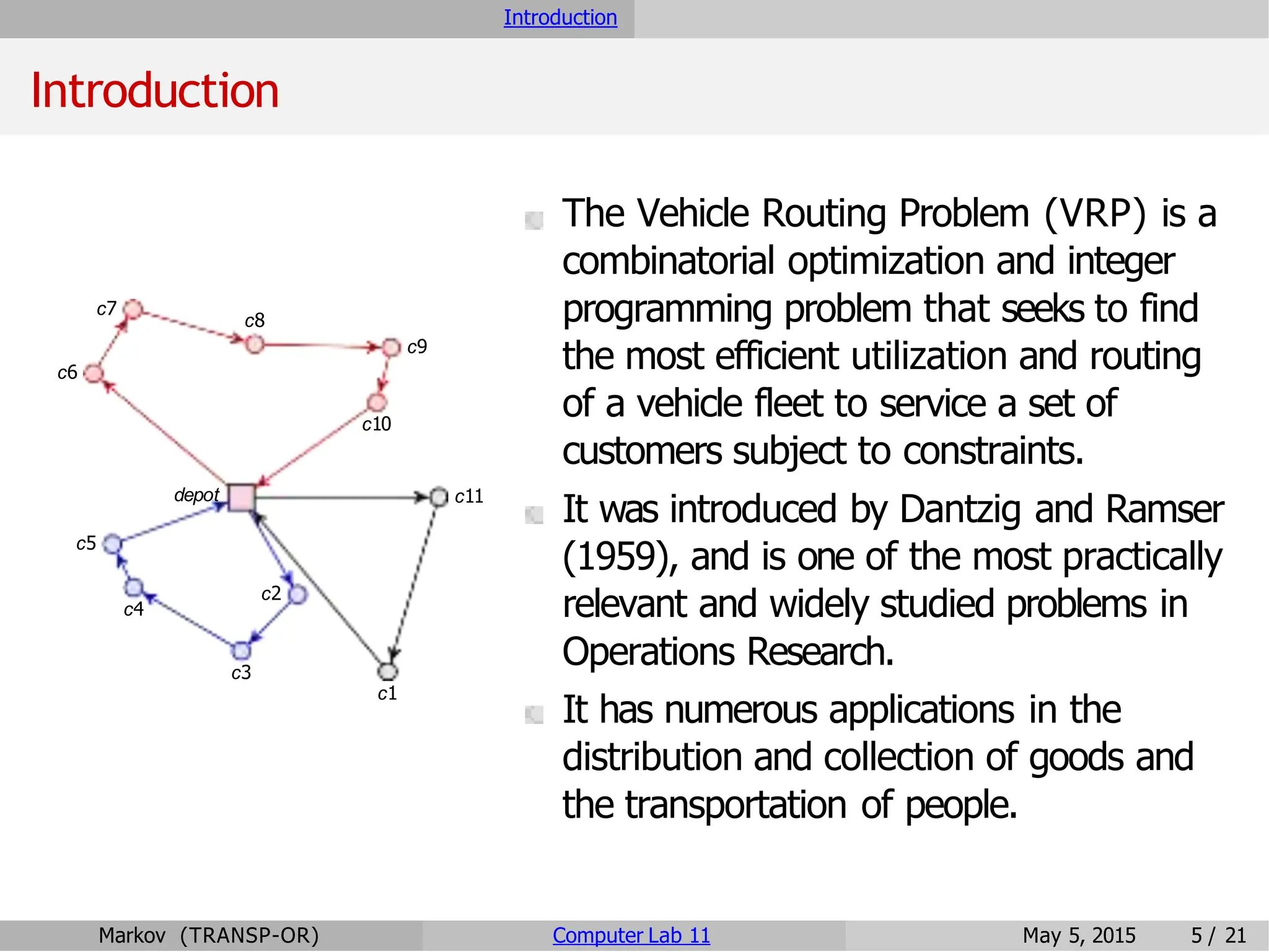
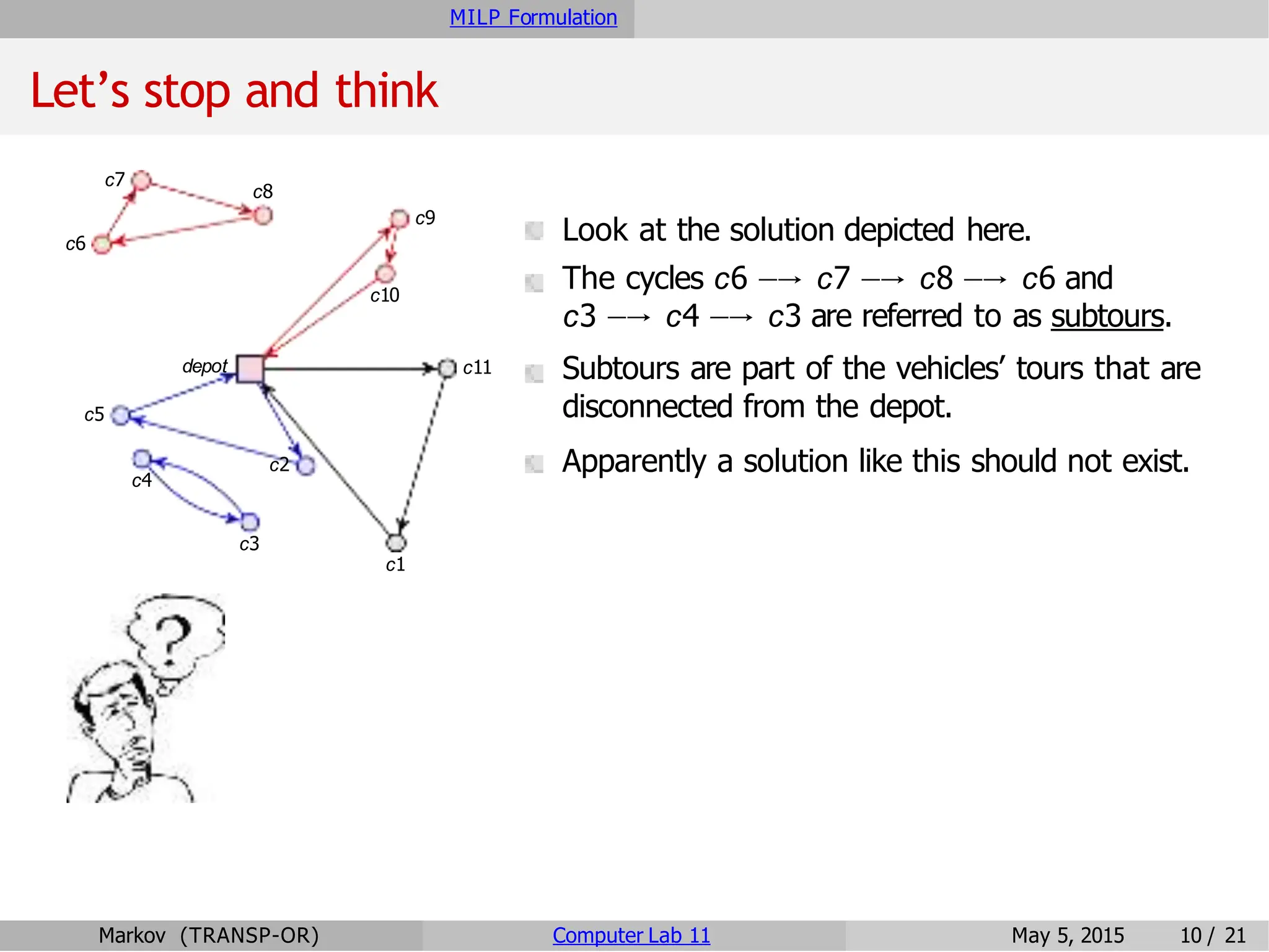
The document discusses the Vehicle Routing Problem (VRP), which is a key combinatorial optimization issue in transportation, aiming to optimize vehicle fleet routes under various constraints. It covers mathematical formulations, including a capacitated VRP model and subtour elimination, as well as various extensions and solution approaches such as exact methods and heuristics. Finally, the document provides an exercise for developing a model using CPLEX to solve a VRP with additional constraints.