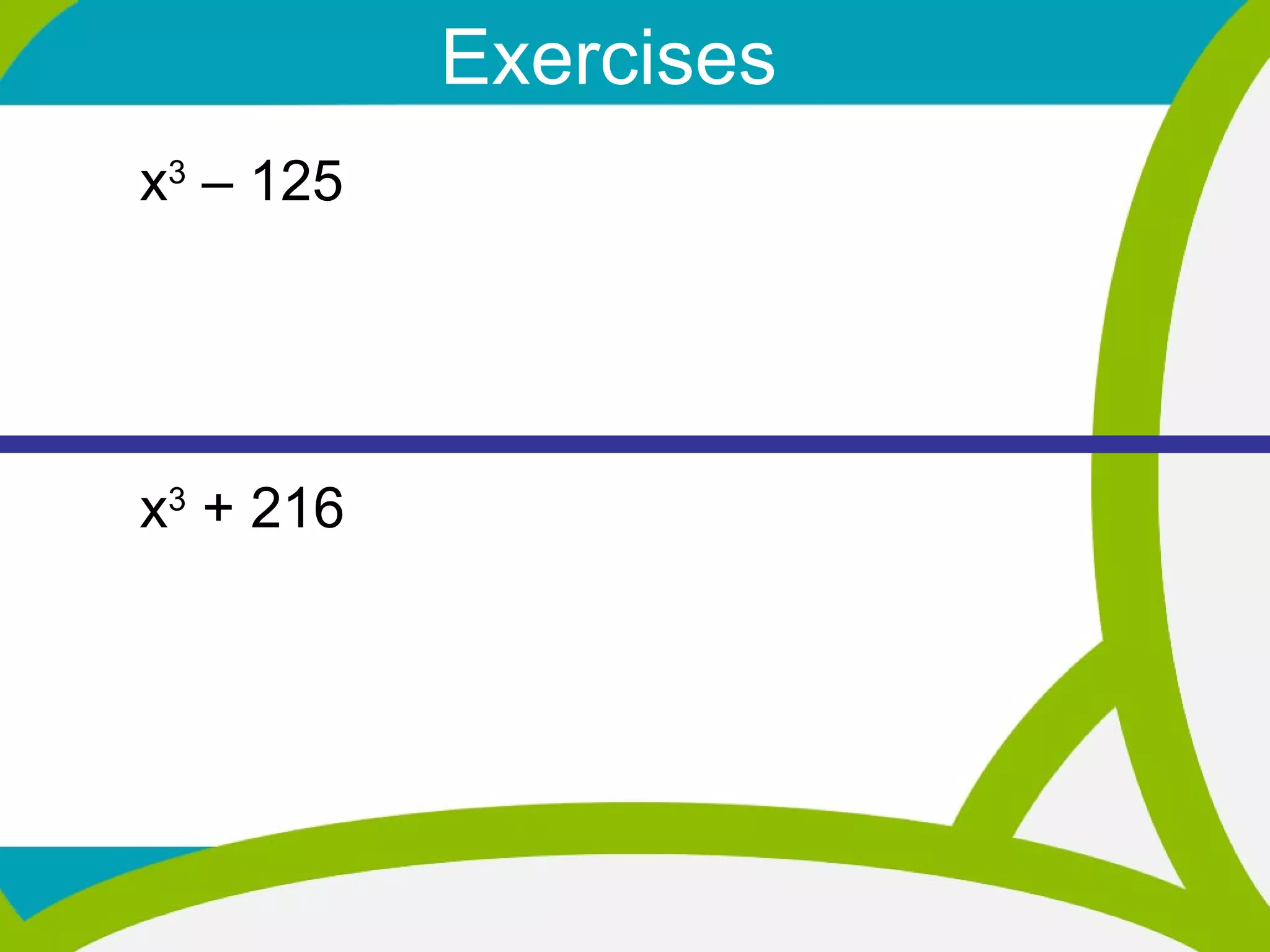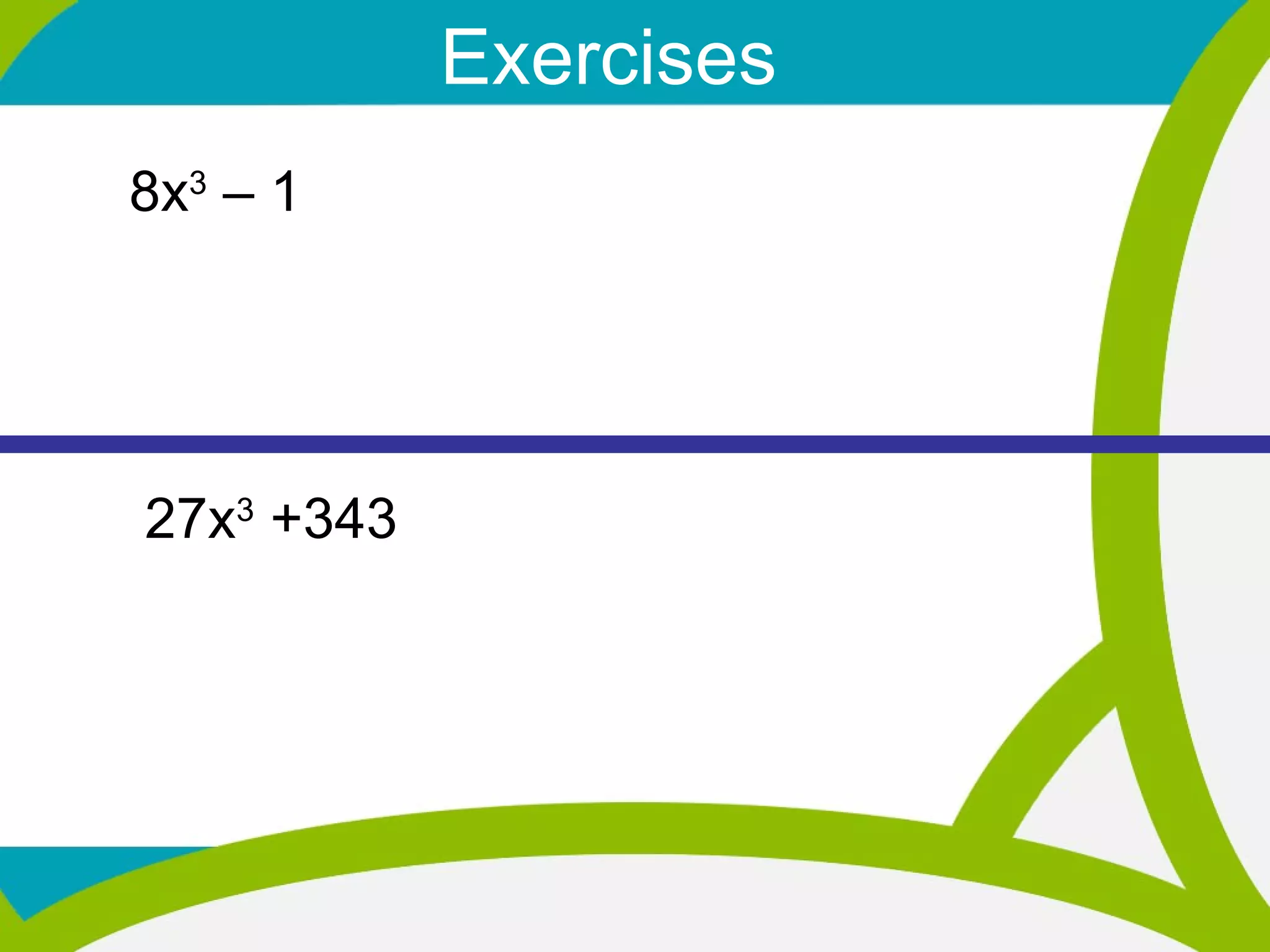The document is about factoring polynomials, specifically factoring the sum and difference of cubes. It provides the formulas for factoring the sum and difference of cubes, along with examples of factoring expressions using those formulas. It also discusses factoring out the greatest common factor from polynomials.




![Sum of two Cubes Example Factor the following: x 3 + 27 a 3 + b 3 = (a + b)(a 2 – ab + b 2 ) x 3 + 27 = (x) 3 + (3) 3 = (x + 3)[(x) 2 − (x)(3) + (3) 2 ] = (x + 3)(x 2 − 3x + 9) 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000…](https://image.slidesharecdn.com/2-27sumdifferenceofcubes-120225222412-phpapp01/75/2-27-12-Special-Factoring-Sum-Difference-of-Two-Cubes-5-2048.jpg)
![Difference of two Cubes Example Factor the following: x 3 - 64 a 3 – b 3 = ( a – b )( a 2 + ab + b 2 ) x 3 - 64 = (x) 3 - (4) 3 = (x - 4)[(x) 2 + (x)(4) + (4) 2 ] = (x - 4)(x 2 +4x + 16) 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000…](https://image.slidesharecdn.com/2-27sumdifferenceofcubes-120225222412-phpapp01/75/2-27-12-Special-Factoring-Sum-Difference-of-Two-Cubes-6-2048.jpg)