This document contains notes from a math lesson on factoring polynomials. It discusses factoring by grouping, where common terms are factored out and then grouped together. It also discusses factoring polynomials into quadratic form when they are raised to higher powers. Examples are provided for both techniques, along with exercises for students to practice factoring by grouping. It concludes with a challenge problem involving factoring a polynomial equation related to the volume of a jewelry box in order to determine its dimensions.

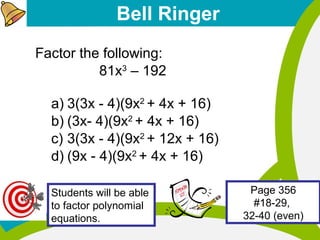
1. Bell Ringer
Factor the following:
81x3
– 192
a) 3(3x - 4)(9x2
+ 4x + 16)
b) (3x- 4)(9x2
+ 4x + 16)
c) 3(3x - 4)(9x2
+ 12x + 16)
d) (9x - 4)(9x2
+ 4x + 16)
Students will be able
to factor polynomial
equations.
Page 356
#18-29,
32-40 (even)

2. Today’s Lesson
Goal: Factor by Grouping & Factor
Polynomials into Quadratic Form
• Factor by Grouping - factors out common
terms, and then groups them.
• For polynomials raised to higher powers,
such as to the fourth power, we can factor
into two quadratics.

3. Factor by Grouping
Pattern:
ra + rb +sa +sb = r(a + b) + s(a + b)
=(r + s)(a + b)

4. Factor by Grouping
• Example 1:
x3
– 3x2
–16x + 48
x2
(x-3) – 16(x – 3)
(x2
– 16)(x-3)

5. Factor by Grouping Exercises
x3
+ 2x2
+ 3x + 6 m3
– 2m2
+ 4m – 8

6. Factor into Quadratic Form
• Recall a quadratic is of the form:
ax2
+ bx2
+ c
• Sometimes with higher powers, we
factor our polynomial into quadratic form.
• Example: x4
– 81
Think of rewriting x4
as (x2
)2
= (x2
+ 9)(x2
– 9)
= (x2
+ 9)(x + 3)(x – 3)

7. Factor into Quadratic Form
16x4
– 81 6y6
– 5y3
– 4

8. Factor into Quadratic Form
• Example 2:
2x8
+ 10x5
+ 12x2
Factor common monomial
= 2x2
(x6
+ 5x3
+ 6)
Factor our trinomial
= 2x2
(x3
+ 3)(x3
+ 2)

9. Challenge Problem
• The dimensions of a jewelry box are:
length 4x, width (x-1), and height (x-2).
If the volume of the box is 24 cubic
inches, find the dimensions of the box.
• Hint: Remember V=lwh. Multiply this
out, and then try factoring by grouping
to solve.
• State the new dimensions,
and show all of your work.

10. Challenge Problem
volume 24 in3
, length 4x, width (x-1), height (x-2)

11. Minute Paper
1) What was the most important topic
you learned today?
2) What did you like/dislike about the
lesson?
3) How could I improve it?

12. Homework
Page 356
#18-29; 32-40 (even)
Factor by Grouping
Factoring into Quadratics
Solve by Factoring