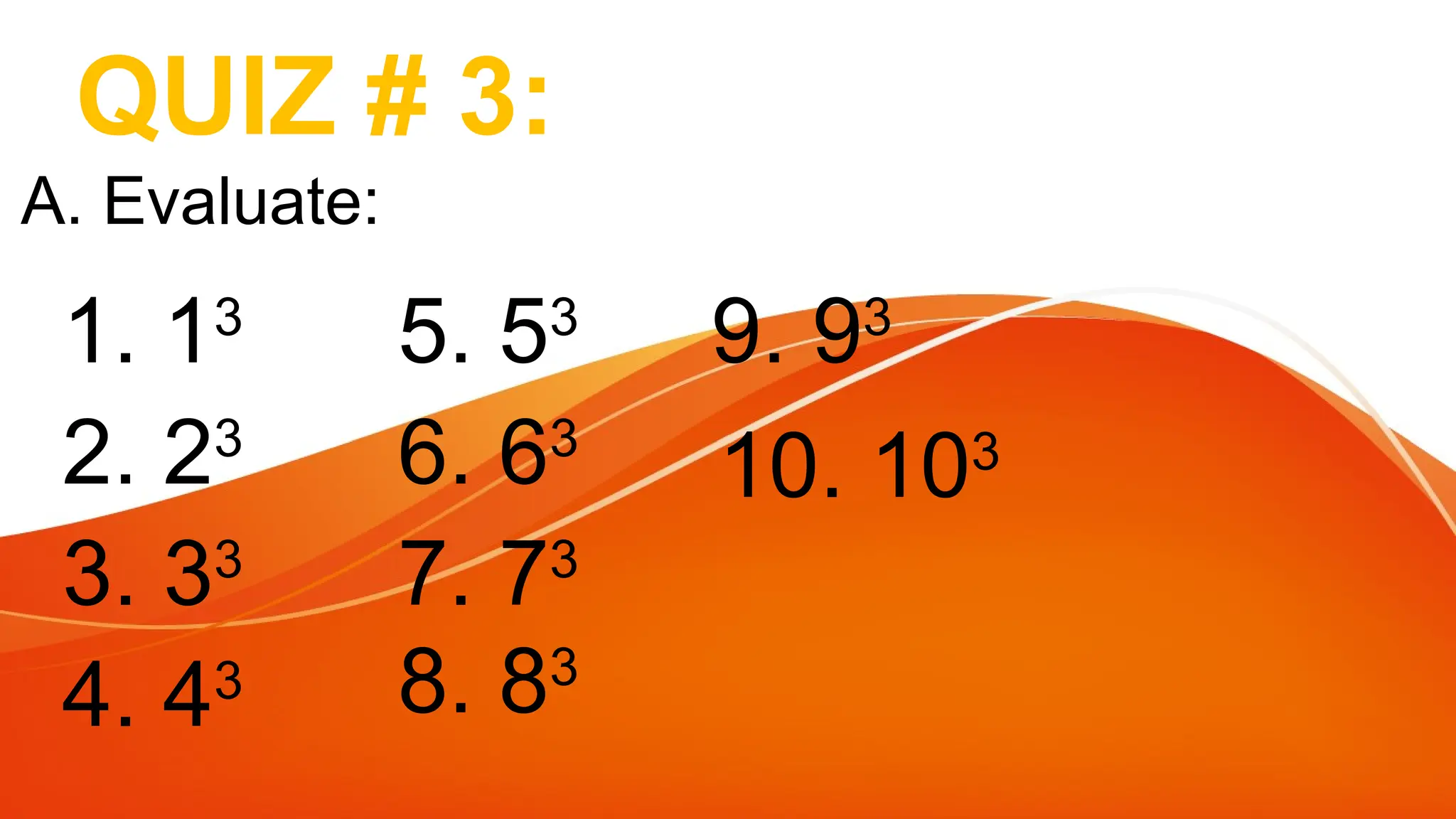
This document outlines the objectives and methods for factoring the sum and difference of two cubes, including relevant formulas and detailed examples. It includes various exercises and quizzes to reinforce the material on factoring polynomials and recognizing differences of squares. Additional notes on perfect squares and complete factoring are also provided.

1. Sum and Difference
of
Two Cubes

2. Objectives: In this lesson, you will
be able to:
Factor the sum and difference of
two cubes completely and

3. EXPLORATION
Complete the following products.
1. (x + 3) (x2
- 3x + 9)
=x3
+____-3x2
-9x+_____+27
=x3
+___

4. EXPLORATION
Complete the following products.
2. (x - 3) (x2
+ 3x + 9)
=___-3x2
+3x2
-___+9x-27
=___ - 27

5. Extension:
SUM AND DIFFERENCE OF TWO CUBES
Let x and y be real numbers, variables,
or algebraic expressions.
Factoring Sum of Two Cubes
Factoring Difference of Two Cubes
x3
+ y3
= (x+y) (x2
-xy+y2
)
x3
- y3
= (x-y) (x2
+xy+y2
)

6. Example 1:
a. a3
+64
Factor each completely
b. 8b3
+ 27c3
= (a +4)(a2
- 4a+16)
= (2b+3c)(4b2
- 6bc+9c2
)
Solution

7. QUIZ # 3:
1. 13
A. Evaluate:
2. 23
3. 33
4. 43
5. 53
6. 63
7. 73
8. 83
9. 93
10. 103

8. Quiz # 3
B. Factor each completely
11. m3
-64
12. 125+8q3
13. t3
-125s3
14. (u3
-8)(u3
+8)
15. 343v3
+ 27w6

9. Note: For a variable to be perfect
square, it must be raised to an
even power. The perfect integer
squares less than 300 are 1, 4, 9,
16, 25, 36, 49, 64, 81, 100, 121,
144, 169, 196, 225, 256, and 289.

10. Example 2:
Factor each completely.
a. 4a2
-
49
b. 9x2
- 25y4
c. 81 - 4p6
q4

11. Try it # 2:
Factor each completely.
a. 9a2
-
49
b. 64x2
- 25y4

12. If the terms of a binomial
have a common factor, first
factor out the common
factor. Then continue
factoring.

13. Example 3
Factor each completely
a. 20x3
- 5x
b. 112-175m4
c. 100x4
- 9x6

14. Try it # 3
Factor each completely
a. 28x3
- 7x
b. 128-200m4

15. After you have factored a difference
of two squares, you can sometimes
continue factoring. Factoring
completely means to continue
factoring until no further factors can
be found.

16. Example 4
Factor each completely
a. 1 - 81x8
b. x4
y8
-z4

17. Try it # 4
Factor each completely
a. 1 - 16x8
b. a4
-625b8

18. Quiz # 3
A. Tell whether or not the given polynomial is a
difference of two squares.
1. a2
- 121
2. c2
- 18
3. d3
- 25
4. 25e2
- 16
5. 49f2
- 2g2
6. 64 +h2
7. 4m4
- 4n2
8. 2 (q2
- 4)
9. r2
- 9s4
10. t14
- u12

19. Quiz # 3
B. Factor each of the following completely
1. a4
- b6
2. c2
- 81
3. 4h2
- 49
4. 16j2
- 81k2
5. 1 - 25q4
6. 16r4
-121
7. 5t3
- 20t
8. 72v - 8v3
9. 144h2
- 49i2
10. (j+k)2
- 400