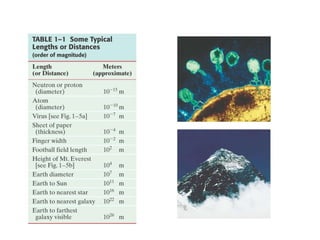
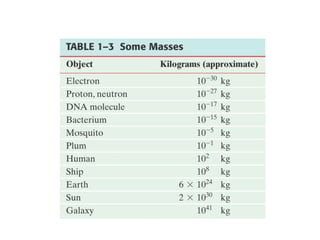
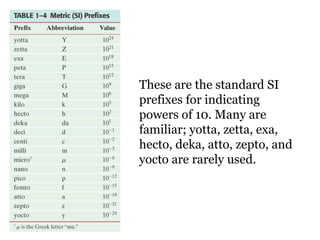
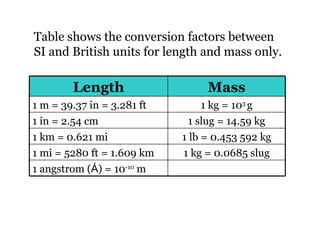
The document discusses units and measurements in physics. It covers the metric and British systems of units, including standard units for length, mass, and time. The metric system is now the most widely used system, known as the International System of Units (SI). The SI base units are the meter, kilogram, and second. Conversion factors allow quantities to be expressed in different units while maintaining the same physical value. Unit analysis ensures quantities in equations have the same dimensions.

1. Unit and Measurement Topic 1

2. Lecture Outline Basic units and quantity Unit conversion Unit analysis

3. Physics and measurement Physics attempts to describe nature in an objective way through measurement Measurement are expressed in units; Officially accepted unit are called standard unit Major systems of unit: Metric cgs system – centimeter, gram, second British (used by the U.S.) – feet, pound, second

4. Basic units and quantity Length, mass and time are the fundamental quantities; combination of them will form all the other unit. Today the most important system is the Syst ème International (SI), which also based on the metric system – meter, kilogram and second

5. Length SI unit of length: meter (m) The original definition: one ten-millionth of the distance from the earth equator to either pole The newest definition: ‘The meter is the length of path traveled by light in vacuum during time interval of 1/299,792,458 of a second’

6. Time SI unit of Time: second (s) The original definition: one second is define as 1/86,400 of a mean solar day (24h/day × 60min/h × 60s/min = 86,400s/day) The newest definition: Time required for 9,192,631,770 periods of radiation emitted by cesium atoms

7. Mass SI unit of mass: kilogram (kg) The original definition: one kilogram is the mass of 0.10 m 3 of water The newest definition: the standard kilogram is a platinum-iridium cylinder kept at he French Bureau of Weights and measurement

11. These are the standard SI prefixes for indicating powers of 10. Many are familiar; yotta, zetta, exa, hecto, deka, atto, zepto, and yocto are rarely used.

12. We will be working in the SI system, in which the basic units are kilograms, meters, and seconds. Quantities not in the table are derived quantities, expressed in terms of the base units.

13. Unit conversion A conversion factor simply lets you express a quantity in terms of other units without changing its physical value or size Example: 1 in. = 2.54 cm. Written another way: 1 = 2.54 cm/in. So if we have measured a length of 21.5 inches, and wish to convert it to centimeters, we use the conversion factor:

14. Table shows the conversion factors between SI and British units for length and mass only. 1 angstrom ( Å) = 10 -10 m 1 kg = 0.0685 slug 1 mi = 5280 ft = 1.609 km 1 lb = 0.453 592 kg 1 km = 0.621 mi 1 slug = 14.59 kg 1 in = 2.54 cm 1 kg = 10 3 g 1 m = 39.37 in = 3.281 ft Mass Length

15. Example 1-2: The 8000-m peaks. The fourteen tallest peaks in the world are referred to as “eight-thousanders,” meaning their summits are over 8000 m above sea level. What is the elevation, in feet, of an elevation of 8000 m?

16. Unit Analysis A powerful way to check your calculation is to use unit analysis Not only must the numerical values on both sides of an equation be equal, the units must be equal as well

17. Dimensions Dimensions of a quantity are the base units that make it up; they are generally written using square brackets. Example: Speed = distance/time Dimensions of speed: [ L / T ] In dimensions, mass, length, time, temperature, and electric current is symbolize with M, L, T, K and A respectively.

18. Dimensional analysis is the checking of dimensions of all quantities in an equation to ensure that those which are added, subtracted, or equated have the same dimensions. Example: Is this the correct equation for velocity? Check the dimensions: Wrong!