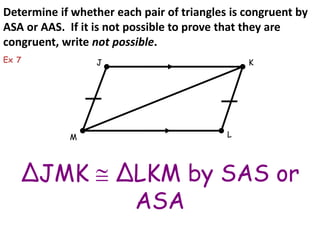
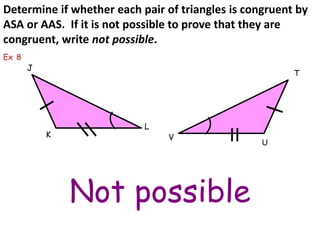
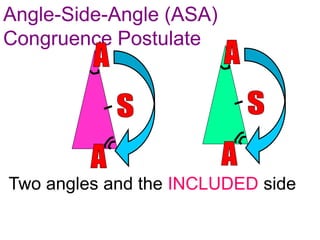
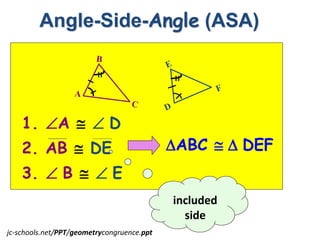
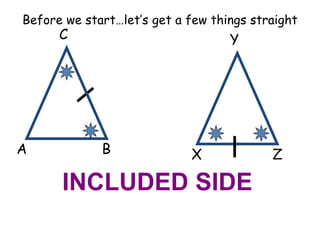
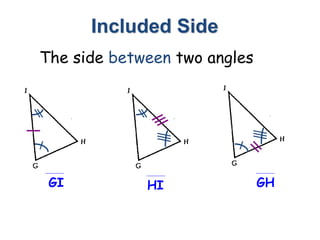
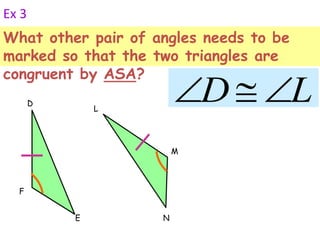
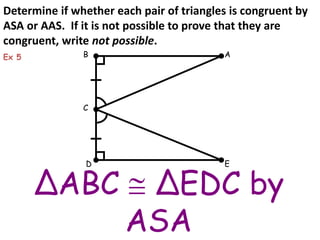
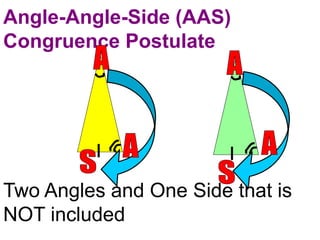
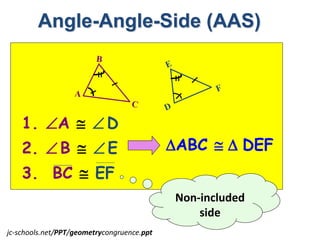
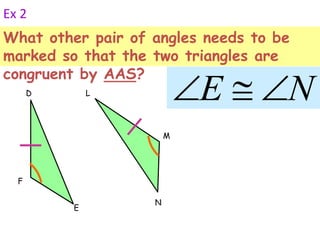
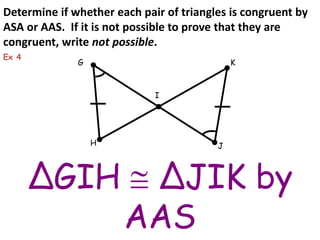
This document discusses two postulates for proving triangles congruent: 1. Angle-Side-Angle (ASA) postulate - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. 2. Angle-Angle-Side (AAS) postulate - If two angles and one non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then the triangles are congruent. 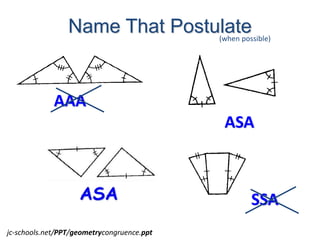The document provides examples of applying these postulates to determine if pairs of triangles are congruent. It also notes there are no AAA or SSA postulates to prove triangles congruent.

1. 5-6
ASA & AAS

2. Proving Triangles
Congruent
jc-schools.net/PPT/geometrycongruence.ppt

3. Angle-Side-Angle (ASA)
Congruence Postulate
Two angles and the INCLUDED side

4. Angle-Side-Angle (ASA)
Postulate 8-3:
If two angles and the included side of
one triangle are congruent to two angles
and the included side of another triangle,
then the two triangles are congruent.

5. Angle-Side-Angle (ASA)
1. A   D
2. AB  DE
3.  B   E
ABC   DEF
included
side
jc-schools.net/PPT/geometrycongruence.ppt

6. Before we start…let’s get a few things straight
C
A B
Y
X Z
INCLUDED SIDE

7. Included Side
The side between two angles
GI HI GH

8. Included Side
Name the included side:
Y and E
E and S
S and Y
E
Y S
YE
ES
SY

9. Angle-Angle-Side (AAS)
Congruence Postulate
Two Angles and One Side that is
NOT included

10. Angle-Angle-Side (AAS)
Theorem 8-1:
If two angles and the nonincluded
side of one triangle are congruent to two
angles and the nonincluded side of
another triangle, then the two triangles
are congruent.

11. Angle-Angle-Side (AAS)
1. A  D
2.  B  E
3. BC  EF
ABC   DEF
Non-included
side
jc-schools.net/PPT/geometrycongruence.ppt

12. Warning: No SSA Postulate
B
There is no such
thing as an SSA
postulate!
A C
E
D
F
NOT CONGRUENT
jc-schools.net/PPT/geometrycongruence.ppt

13. Warning: No AAA Postulate
B
A C
E
D
F
There is no such
thing as an AAA
postulate!
NOT CONGRUENT
jc-schools.net/PPT/geometrycongruence.ppt

14. }Your Only Ways
To Prove
Triangles Are
Congruent

15. Name That Postulate
(when possible)
ASA
AAA
SSA
jc-schools.net/PPT/geometrycongruence.ppt

16. Things you can mark on a triangle when they aren’t
marked.
Overlapping sides are
congruent in each
triangle by the
REFLEXIVE property
Vertical
Angles are
congruent
Alt Int
Angles are
congruent
given
parallel lines

17. Ex 1
ΔDEF ΔLMN D N DE NL
In and , , and
E L
. Write a congruence statement.
  
   
 D E F   N L M

18. Ex 2
What other pair of angles needs to be
marked so that the two triangles are
congruent by AAS?
F
D
E
M
L
N
E N

19. Ex 3
What other pair of angles needs to be
marked so that the two triangles are
congruent by ASA?
F
D
E
M
L
N
DL

20. Determine if whether each pair of triangles is congruent by
ASA or AAS. If it is not possible to prove that they are
congruent, write not possible.
ΔGIH  ΔJIK by
AAS
G
I
H J
K
Ex 4

21. Determine if whether each pair of triangles is congruent by
ASA or AAS. If it is not possible to prove that they are
congruent, write not possible.
B A
ΔABC  ΔEDC by
ASA
C
D E
Ex 5

22. Determine if whether each pair of triangles is congruent by
ASA or AAS. If it is not possible to prove that they are
congruent, write not possible.
J K
M L
ΔJMK  ΔLKM by SAS or
ASA
Ex 7

23. Determine if whether each pair of triangles is congruent by
ASA or AAS. If it is not possible to prove that they are
congruent, write not possible.
Not possible
K
J
L
T
U
Ex 8
V