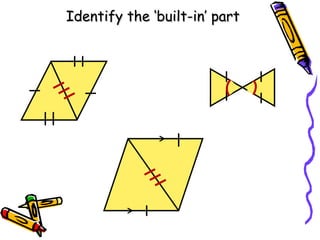
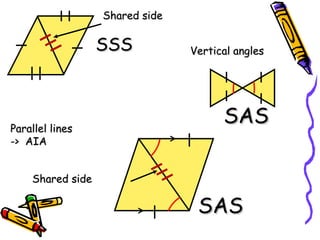
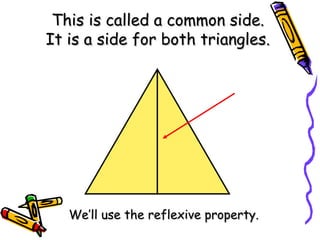
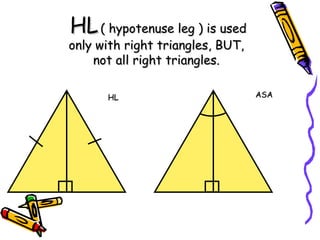
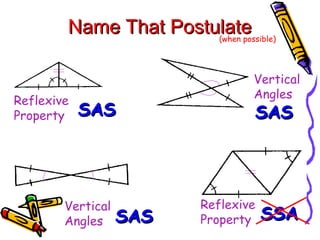
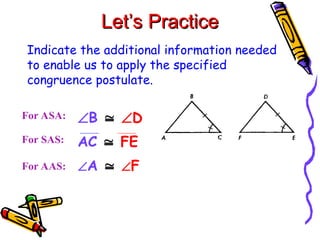
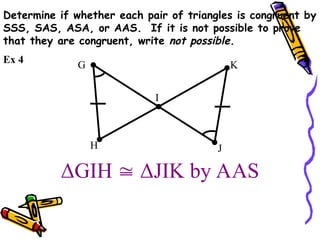
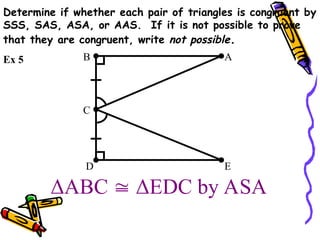
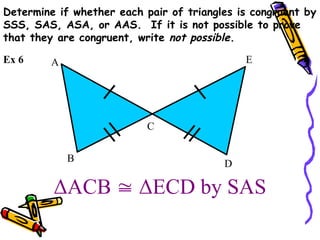
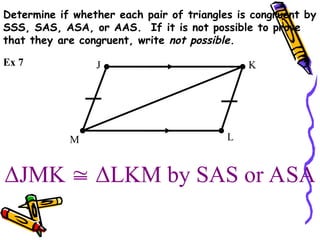
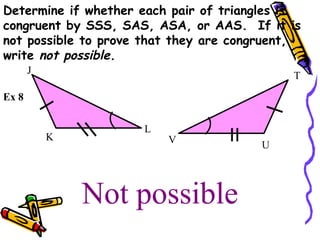
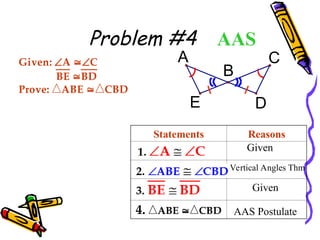
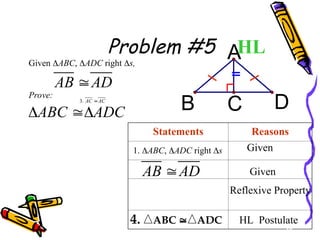
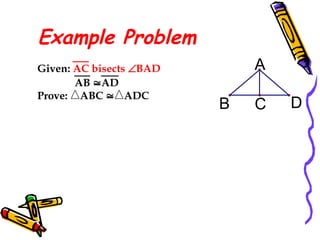
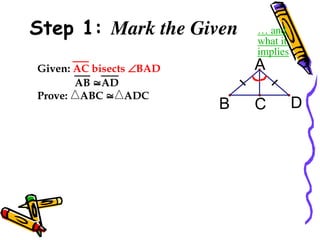
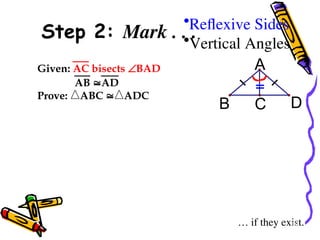
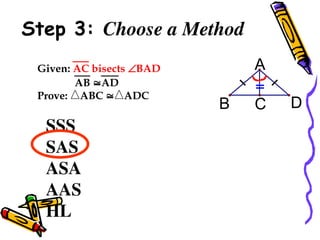
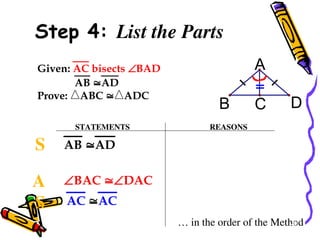
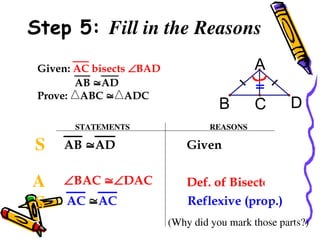
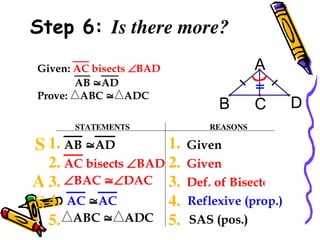
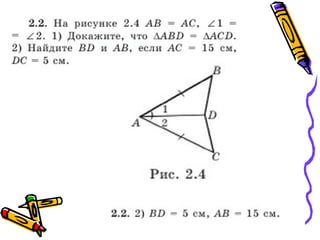
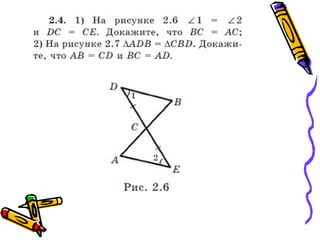
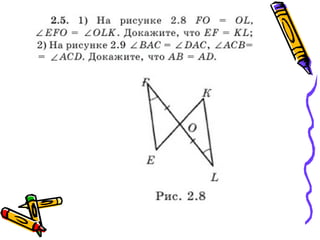
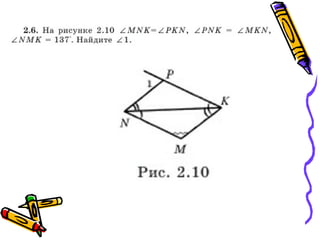
The document outlines methods for proving the congruence of triangles, including postulates like SSS, SAS, ASA, AAS, and HL specifically for right triangles. It describes the necessary additional information and common properties such as reflexive and vertical angles that aid in proving congruence. The document also provides examples and steps for constructing congruence proofs.

1. Proving Triangles
Congruent

2. Triangle Congruency Short-Cuts
If you can prove one of the following short
cuts, you have two congruent triangles
1.SSS (side-side-side)
2.SAS (side-angle-side)
3.ASA (angle-side-angle)
4.AAS (angle-angle-side)
5.HL (hypotenuse-leg) right triangles only!

3. Built – In Information in
Triangles

4. Identify the ‘built-in’ part
Identify the ‘built-in’ part

5. Shared side
Shared side
Parallel lines
Parallel lines
-> AIA
-> AIA
Shared side
Shared side
Vertical angles
Vertical angles
SAS
SAS
SAS
SAS
SSS
SSS

6. SOME REASONS For Indirect
SOME REASONS For Indirect
Information
Information
• Def of midpoint
Def of midpoint
• Def of a bisector
Def of a bisector
• Vert angles are congruent
Vert angles are congruent
• Def of perpendicular bisector
Def of perpendicular bisector
• Reflexive property (shared side)
Reflexive property (shared side)
• Parallel lines ….. alt int angles
Parallel lines ….. alt int angles
• Property of Perpendicular Lines
Property of Perpendicular Lines

7. This is called a common side.
This is called a common side.
It is a side for both triangles.
It is a side for both triangles.
We’ll use the reflexive property.
We’ll use the reflexive property.

8. HL
HL( hypotenuse leg ) is used
( hypotenuse leg ) is used
only with right triangles, BUT,
only with right triangles, BUT,
not all right triangles.
not all right triangles.
HL
HL ASA
ASA

9. Name That Postulate
Name That Postulate
(when possible)
SAS
SAS
SAS
SAS
SAS
SAS
Reflexive
Property
Vertical
Angles
Vertical
Angles
Reflexive
Property SSA
SSA

10. Let’s Practice
Let’s Practice
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
For SAS:
B  D
For AAS: A  F
AC  FE

11. Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.
ΔGIH  ΔJIK by AAS
G
I
H J
K
Ex 4

12. ΔABC  ΔEDC by ASA
B A
C
E
D
Ex 5
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

13. ΔACB  ΔECD by SAS
B
A
C
E
D
Ex 6
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

14. ΔJMK  ΔLKM by SAS or ASA
J K
L
M
Ex 7
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

15. Not possible
K
J
L
T
U
Ex 8
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is
not possible to prove that they are congruent,
write not possible.
V

16. Problem #4
Statements Reasons
AAS
Given
Given
Vertical Angles Thm
AAS Postulate
Given: A C
BE BD
Prove: ABE  CBD
E
C
D
A
B
4. ABE  CBD
37

17. Problem #5
3. AC AC

Statements Reasons
C
B D
AHL
Given
Given
Reflexive Property
HL Postulate
4. ABC  ADC
1. ABC, ADC right s
AB AD

Given ABC, ADC right s,
Prove:
AB AD

ABC ADC
 
38

18. Congruence Proofs
1. Mark the Given.
2. Mark …
Reflexive Sides or Angles / Vertical Angles
Also: mark info implied by given info.
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
39

19. Given implies Congruent
Parts
midpoint
parallel
segment bisector
angle bisector
perpendicular
segments

angles

segments

angles

angles

40

20. Example Problem
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
41

21. Step 1: Mark the Given … and
what it
implies
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
42

22. •Reflexive Sides
•Vertical Angles
Step 2: Mark . . .
… if they exist.
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
43

23. Step 3: Choose a Method
SSS
SAS
ASA
AAS
HL
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
44

24. Step 4: List the Parts
STATEMENTS REASONS
… in the order of the Method
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
BAC DAC
AB AD
AC AC
S
A
S
45

25. Step 5: Fill in the Reasons
(Why did you mark those parts?)
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
BAC DAC
AB AD
AC AC
Given
Def. of Bisector
Reflexive (prop.)
S
A
S
46

26. S
A
S
Step 6: Is there more?
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB AD
Prove: ABC  ADC
BAC DAC
AB AD
AC AC
Given
AC bisects BAD Given
Def. of Bisector
Reflexive (prop.)
ABC  ADC SAS (pos.)
1.
2.
3.
4.
5.
1.
2.
3.
4.
5. 47

27. Congruent Triangles Proofs
1. Mark the Given and what it implies.
2. Mark … Reflexive Sides / Vertical Angles
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
53

28. Решение задач по
Решение задач по
учебнику геометрия 7
учебнику геометрия 7
класс Шыныбеков
класс Шыныбеков

33. HOMEWORK
Повторить теоретический материал
Геометрия 7 класс, Шыныбеков
Стр. 33 № 2.3
Стр. 34 № 2.7