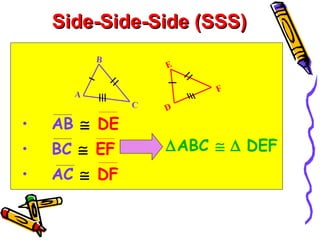
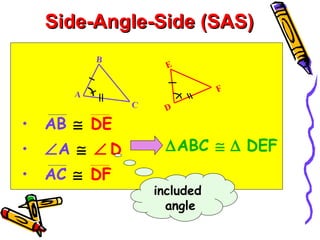
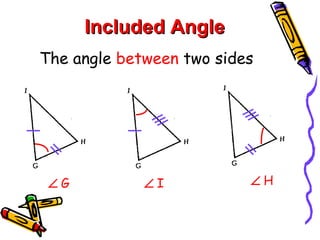
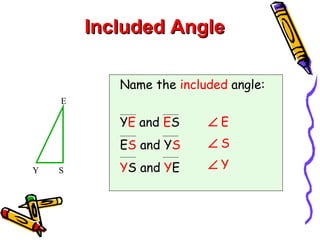
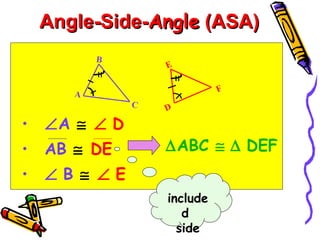
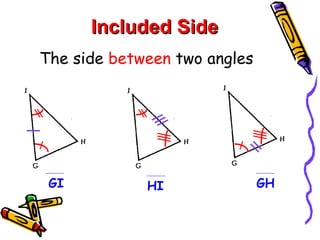
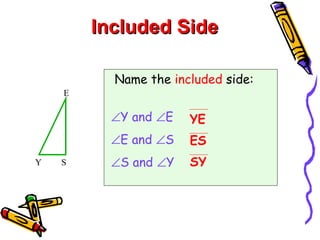
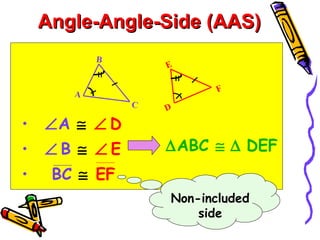
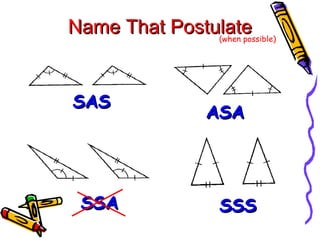
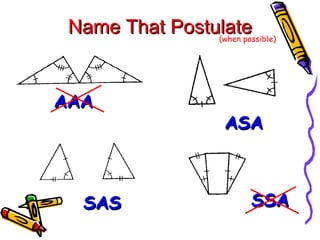
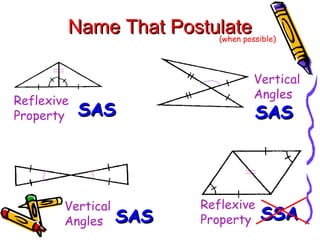
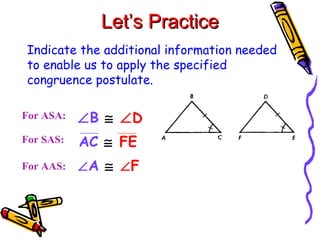
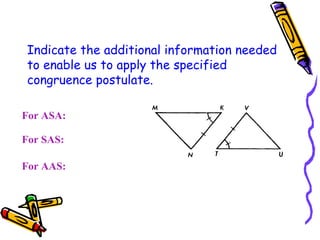
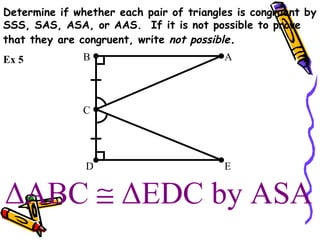
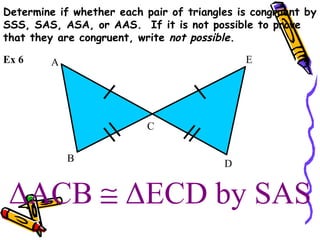
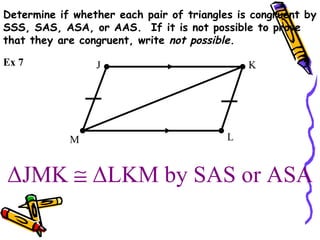
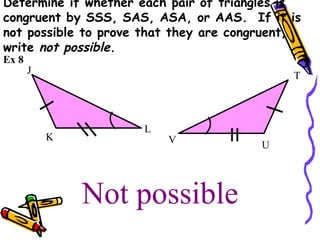
This document discusses different ways to prove that two triangles are congruent, including the side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), and angle-angle-side (AAS) congruence postulates. It provides examples of applying each postulate to determine if pairs of triangles are congruent or not. There is no side-side-angle (SSA) or angle-angle-angle (AAA) postulate that can prove congruence.

1. Proving Triangles Congruent Free powerpoints at http://www.worldofteaching.com

2. Two geometric figures with exactly the same size and shape. The Idea of a Congruence A C B D E F

3. How much do you need to know. . . . . . about two triangles to prove that they are congruent?

4. In Lesson 4.2, you learned that if all six pairs of corresponding parts (sides and angles) are congruent, then the triangles are congruent. Corresponding Parts  ABC   DEF B A C E D F AB  DE BC  EF AC  DF  A   D  B   E  C   F

5. Do you need all six ? NO !

6. Side-Side-Side (SSS) AB  DE BC  EF AC  DF  ABC   DEF B A C E D F

7. Side-Angle-Side (SAS) AB  DE  A   D AC  DF  ABC   DEF B A C E D F included angle

8. The angle between two sides Included Angle  G  I  H

9. Name the included angle: Y E and E S E S and Y S Y S and Y E Included Angle  E  S  Y S Y E

10. Angle-Side- Angle (ASA)  A   D AB  DE  B   E  ABC   DEF B A C E D F included side

11. The side between two angles Included Side GI HI GH

12. Name the included side:  Y and  E  E and  S  S and  Y Included Side YE ES SY S Y E

13. Angle-Angle-Side (AAS)  A   D  B   E BC  EF  ABC   DEF B A C E D F Non-included side

14. Warning: No SSA Postulate A C B D E F NOT CONGRUENT There is no such thing as an SSA postulate!

15. Warning: No AAA Postulate A C B D E F There is no such thing as an AAA postulate! NOT CONGRUENT

16. The Congruence Postulates SSS correspondence ASA correspondence SAS correspondence AAS correspondence SSA correspondence AAA correspondence

17. Name That Postulate SAS ASA SSS SSA (when possible)

18. Name That Postulate (when possible) ASA SAS AAA SSA

19. Name That Postulate (when possible) SAS SAS SAS Reflexive Property Vertical Angles Vertical Angles Reflexive Property SSA

20. Name That Postulate (when possible)

21. (when possible) Name That Postulate

22. Let’s Practice Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: For SAS:  B   D For AAS:  A   F AC  FE

23. Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: For SAS: For AAS:

24. Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible . Δ GIH  Δ JIK by AAS Ex 4 G I H J K

25. Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible . Δ ABC  Δ EDC by ASA Ex 5 B A C E D

26. Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible . Δ ACB  Δ ECD by SAS B A C E D Ex 6

27. Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible . Δ JMK  Δ LKM by SAS or ASA J K L M Ex 7

28. Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible . Not possible K J L T U Ex 8 V

29. WORK