Download as PDF, PPTX
![対数尤度関数を定義する
funQ <- function(beta1, beta2, beta3, x){
1 / (1 + exp(-(beta1 + beta2*x$x + beta3*x$f)))
}
logLikelyhood.part <- function(beta1, beta2, beta3, x){
log(choose(x$N, x$y))+x$y*log(funQ(beta1, beta2, beta3, x))+(x$N-x$y)*log(1-funQ(beta1,
beta2, beta3, x))
}
logLikelyhood <- function(param){
beta1 <- param[1]
beta2 <- param[2]
beta3 <- param[3]
tmp <- 0
for(i in 1:nrow(data4a)){
tmp <- tmp + logLikelyhood.part(beta1, beta2, beta3, data4a[i,])
}
return(tmp)
}](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-17-320.jpg)
![optimで対数尤度の最大値を求める
> optim(c(1,1,1), logLikelyhood, control=list(fnscale=-1))
$par
[1] -19.537817 1.952571 2.022927
$value
[1] -133.1056
$counts
function gradient
228 NA
$convergence
[1] 0
$message
NULL
これらが推定値になる。
glmの結果
Coefficients:
(Intercept) x fT
-19.536 1.952 2.022](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-18-320.jpg)
![ヘッセ行列を求める
rslt <- NULL
for(hen in c(b11, b12, b13, b21, b22, b23, b31, b32, b33)){
tmp <- 0
for(i in 1:nrow(data4a)){
N <- data4a[i,]$N
y <- data4a[i,]$y
x <- data4a[i,]$x
z <- data4a[i,]$f
tmp <- tmp + eval(hen)
}
rslt <- c(rslt, tmp)
}
hessian <- -matrix(rslt, 3,3 )](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-20-320.jpg)
![逆行列を求める
> solve(hessian)
[,1] [,2] [,3]
[1,] 1.9991552 -0.19551996 -0.19765617
[2,] -0.1955200 0.01928951 0.01778859
[3,] -0.1976562 0.01778859 0.05351702](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-21-320.jpg)
![対角行列の平方根を求める
> (se <- sqrt(diag(solve(hessian))))
[1] 1.4139149 0.1388867 0.2313375
これらが標準誤差になる。
glmの結果
Std. Error
1.4138
0.1389
0.2313](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-22-320.jpg)
![z統計量を求める
> (zvalue <- c(b1, b2, b3)/ se)
[1] -13.818242 14.058736 8.744485
glmの結果
z value
-13.82
14.06
8.74](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-23-320.jpg)
![glmの結果
Pr(>|z|) Pr(>|z|)
<2e-16 ***
<2e-16 ***
<2e-16 ***を求める
> pnorm(abs(zvalue), lower.tail=F)
[1] 9.892197e-44 3.404587e-45 1.120176e-18
glmを使わずに、推定できた。](https://image.slidesharecdn.com/midori6av2-140729060548-phpapp02/85/slide-24-320.jpg)
More Related Content
![[The Elements of Statistical Learning]Chapter8: Model Inferennce and Averaging](https://cdn.slidesharecdn.com/ss_thumbnails/theelementsofstatisticallearningchapter8modelinferennceandaveraging-181109001318-thumbnail.jpg?width=640&height=640&fit=bounds)
![[The Elements of Statistical Learning]Chapter18: High Dimensional Problems](https://cdn.slidesharecdn.com/ss_thumbnails/theelementsofstatisticallearningchapter18highdimensionalproblems-181109005557-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to 第六回「データ解析のための統計モデリング入門」前半
![[PRML] パターン認識と機械学習（第1章：序論）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter1-170903070406-thumbnail.jpg?width=640&height=640&fit=bounds)
第六回「データ解析のための統計モデリング入門」前半
- 1.
- 2. 自己紹介 • 電気通信大学大学院 修士2年 •専門：信頼性工学、生存時間解析
- 3. 6.1 さまざまな種類のデータで応用できるGLM • GLMの特徴 •確率分布・リンク関数・線形予測子の組み合わ せを指定することによって、さまざまなタイプの データを表現できる 確率分布 乱数生成 glm()のfamily 指定 よく使うリン ク関数 （離散） 二項分布 rbinom() binomial logit ポアソン分布 rpois() poisson log 負の二項分布 rnbinom() (glm.nb()関数) log (連続) ガンマ分布 rgamma() gamma logかな？ 正規分布 rnomd() Gaussian identity
- 4. 6.2 例題：上限のあるカウントデータ • 二項分布を使う •応答変数𝑦 ∈ {0, 1, 2, … , 𝑁}の範囲の値をとる • 「N個体の実験対象に同じ処理をしたら、y個体で 反応が陽性、N-y個体では陰性」
- 5. 例題のデータ N y xf 8 1 9.8 C 8 6 10 C 8 5 11 C 8 6 11 C 8 1 9.4 C 8 1 8.8 C ・・・ ・・・ ・・・ ・・・ • 𝑁𝑖個の観察種子のうち生きていて発芽能力がある ものは𝑦𝑖個、死んだ種子は𝑁𝑖 − 𝑦𝑖個 • xは体サイズ • fは肥料の有無。Cは肥料なし、Tは肥料あり > summary(data4a) N y x f Min. :8 Min. :0.00 Min. : 7.660 C:50 1st Qu. :8 1st Qu. :3.00 1st Qu. : 9.338 T:50 Median :8 Median :6.00 Median: 9.965 Mean :8 Mean :5.08 Mean : 9.967 3rd Qu. :8 3rd Qu. :8.00 3rd Qu.:10.770 Max. :8 Max. :8.00 Max. :12.440 表: データ例
- 6.
- 7. 6.3 二項分布で表現する「あり・なし」カウントデータ • 二項分布の確率分布 N個中のy個で事象が生起する確率 𝑝𝑦 𝑁, 𝑞 = 𝑁 𝑦 𝑞 𝑦 1 − 𝑞 𝑁−𝑦 確率𝑝(𝑦𝑖|8,𝑞) 𝑦𝑖 ー：q=0.1 ー：q=0.3 ー：q=0.8
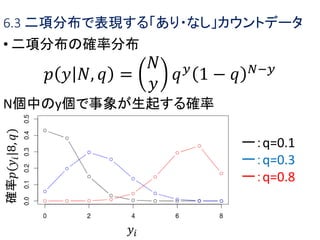
- 8. 6.4 ロジスティック回帰とロジットリンク関数 線形予測子𝑧 確率𝑞 𝑞𝑖 =𝑙𝑜𝑔𝑖𝑠𝑡𝑖𝑐 𝑧𝑖 = 1 1 + exp(−𝑧𝑖) • 6.4.1 ロジットリンク関数 種子の生存確率𝑞𝑖をパラメータにする
- 9. • ロジスティック関数と線形予測子𝑧𝑖 =𝛽1 + 𝛽2 𝑥𝑖の 関係を見る 𝛽1 = 2 𝛽1 = 0 𝛽1 = −3 𝛽2 = 4 𝛽2 = 2 𝛽1 = −1 確率𝑞 確率𝑞 説明変数𝑥 説明変数𝑥 𝛽2 = 2の時 𝛽1 = 0の時
- 10. 6.4.2 パラメータ推定 𝐿 𝛽𝑗= 𝑖 𝑁𝑖 𝑦𝑖 𝑞𝑖 𝑦 𝑖 1 − 𝑞𝑖 𝑁 𝑖−𝑦 𝑖 log(𝐿 𝛽𝑗 = 𝑖 𝑙𝑜𝑔 𝑁𝑖 𝑦𝑖 + 𝑦𝑖 log 𝑞𝑖 + 𝑁𝑖 − 𝑦𝑖 log(1 − 𝑞𝑖) 尤度関数 対数尤度関数 対数尤度関数を最大にする推定値のセット{ 𝛽𝑗}を 探し出す。 最尤法
- 11. > model <-glm(cbind(y, N-y)~x+f, data=data4a, family=binomial) > model Call: glm(formula = cbind(y, N - y) ~ x + f, family = binomial, data = data4a) Coefficients: (Intercept) x fT -19.536 1.952 2.022 Degrees of Freedom: 99 Total (i.e. Null); 97 Residual Null Deviance: 499.2 Residual Deviance: 123 AIC: 272.2 6.4.2 パラメータ推定
- 12.
- 13. 6.4.3 ロジットリンク関数の意味・解釈 𝑞𝑖 1 −𝑞𝑖 = exp 線形予測子 = exp(𝛽1 + 𝛽2 𝑥𝑖 + 𝛽3 𝑓𝑖) = exp 𝛽1 exp 𝛽2 exp(𝛽3) ロジスティック関数：𝑞𝑖 = 1 1+exp(−𝑧 𝑖) ロジット関数：𝑙𝑜𝑔𝑖𝑡 𝑞𝑖 = log 𝑞 𝑖 1−𝑞𝑖 = 𝑧𝑖 変換 オッズ 生存する確率 生存しない確率 𝑞𝑖 = 0.5ならオッズは1倍 𝑞𝑖 = 0.8ならオッズは4倍
- 14. 𝑞𝑖 1 − 𝑞𝑖 =exp −19.5 exp 1.95𝑥𝑖 exp(2.02𝑓𝑖) 𝑥𝑖が1単位増加したらexp(1.95 𝑥𝑖 + 1 )になる。 exp 1.95 ≈ 7 オッズが7倍ぐらい増加する。 「病気であれば、発病リスクが7倍になる」と 表現されることがある。
- 15.
- 16.
- 17. 対数尤度関数を定義する funQ <- function(beta1,beta2, beta3, x){ 1 / (1 + exp(-(beta1 + beta2*x$x + beta3*x$f))) } logLikelyhood.part <- function(beta1, beta2, beta3, x){ log(choose(x$N, x$y))+x$y*log(funQ(beta1, beta2, beta3, x))+(x$N-x$y)*log(1-funQ(beta1, beta2, beta3, x)) } logLikelyhood <- function(param){ beta1 <- param[1] beta2 <- param[2] beta3 <- param[3] tmp <- 0 for(i in 1:nrow(data4a)){ tmp <- tmp + logLikelyhood.part(beta1, beta2, beta3, data4a[i,]) } return(tmp) }
- 18. optimで対数尤度の最大値を求める > optim(c(1,1,1), logLikelyhood,control=list(fnscale=-1)) $par [1] -19.537817 1.952571 2.022927 $value [1] -133.1056 $counts function gradient 228 NA $convergence [1] 0 $message NULL これらが推定値になる。 glmの結果 Coefficients: (Intercept) x fT -19.536 1.952 2.022
- 19. それぞれの２階微分を求める f <- expression( y*log(1/(1+exp(-b1-b2*x-b3*z))) +(N-y)*log(1-1/(1+exp(-b1-b2*x-b3*z))) ) b11 <- D(D(f, "b1"),"b1") b12 <- D(D(f, "b1"),"b2") b13 <- D(D(f, "b1"),"b3") b21 <- D(D(f, "b2"),"b1") b22 <- D(D(f, "b2"),"b2") b23 <- D(D(f, "b2"),"b3") b31 <- D(D(f, "b3"),"b1") b32 <- D(D(f, "b3"),"b2") b33 <- D(D(f, "b3"),"b3") b1 <- -19.537817 b2 <- 1.952571 b3 <- 2.022927 の推定値の定義も忘れずに
- 20. ヘッセ行列を求める rslt <- NULL for(henin c(b11, b12, b13, b21, b22, b23, b31, b32, b33)){ tmp <- 0 for(i in 1:nrow(data4a)){ N <- data4a[i,]$N y <- data4a[i,]$y x <- data4a[i,]$x z <- data4a[i,]$f tmp <- tmp + eval(hen) } rslt <- c(rslt, tmp) } hessian <- -matrix(rslt, 3,3 )
- 21. 逆行列を求める > solve(hessian) [,1] [,2][,3] [1,] 1.9991552 -0.19551996 -0.19765617 [2,] -0.1955200 0.01928951 0.01778859 [3,] -0.1976562 0.01778859 0.05351702
- 22. 対角行列の平方根を求める > (se <-sqrt(diag(solve(hessian)))) [1] 1.4139149 0.1388867 0.2313375 これらが標準誤差になる。 glmの結果 Std. Error 1.4138 0.1389 0.2313
- 23. z統計量を求める > (zvalue <-c(b1, b2, b3)/ se) [1] -13.818242 14.058736 8.744485 glmの結果 z value -13.82 14.06 8.74
- 24. glmの結果 Pr(>|z|) Pr(>|z|) <2e-16 *** <2e-16*** <2e-16 ***を求める > pnorm(abs(zvalue), lower.tail=F) [1] 9.892197e-44 3.404587e-45 1.120176e-18 glmを使わずに、推定できた。
- 25.