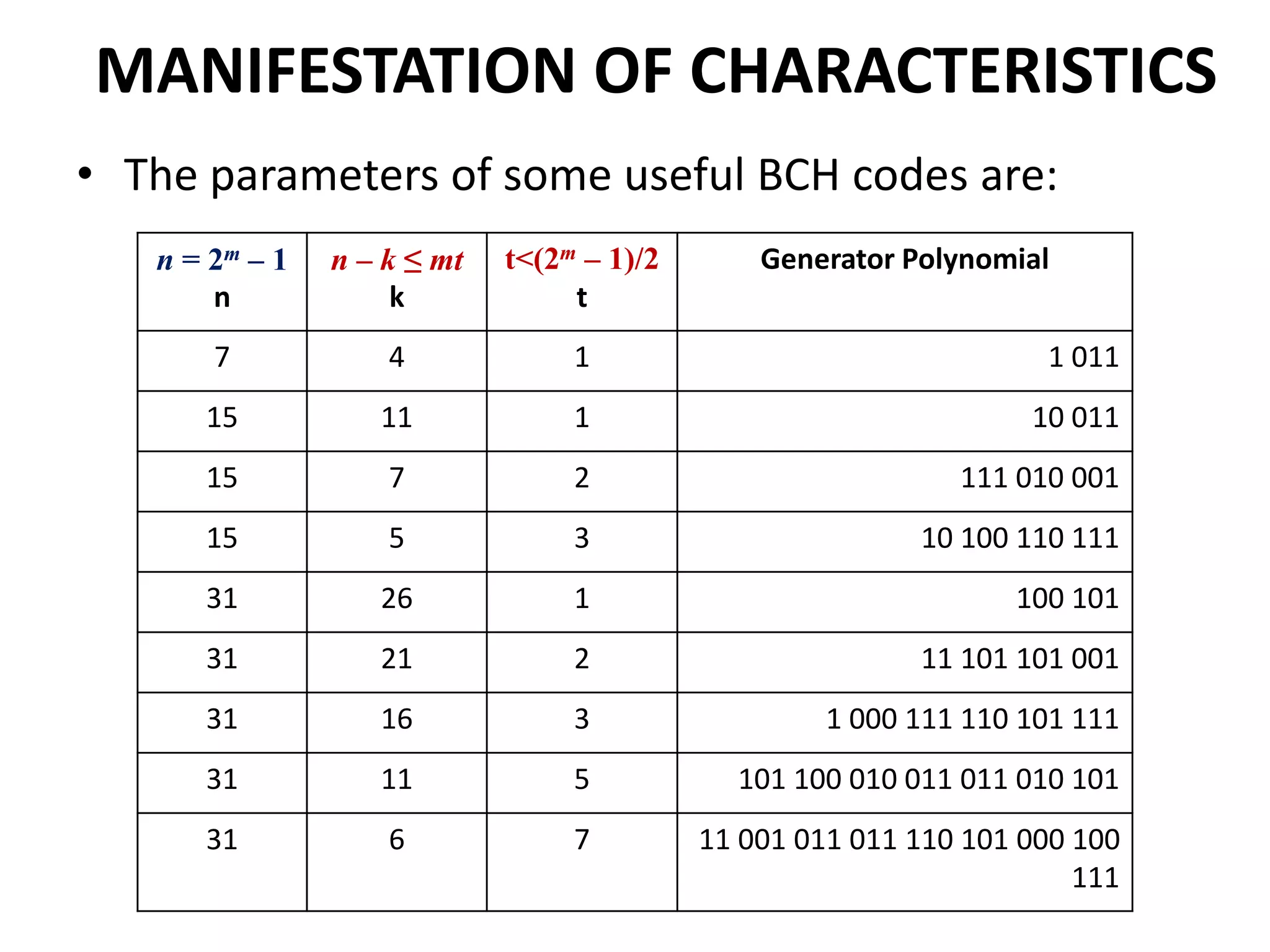
This document provides information about BCH codes, including: 1. BCH codes are linear cyclic block codes that can detect and correct errors. They allow flexibility in choosing block length and code rate. 2. Key characteristics of BCH codes include the block length being 2m - 1, error correction ability up to t errors where t<(2m - 1)/2, and minimum distance of at least 2t + 1. 3. Galois fields are finite fields that are important for constructing BCH codes. A generator polynomial is chosen based on the roots in the Galois field and is used to encode messages into codewords.

1. BCH CODES

2. HISTORY

3. WHY CODING ?

4. • 2 Key system parameters available for designer
– Ch BW
– Transmitted Sig Power
• Hence we go for modulation schemes but error
performance is an issue – hence error control coding
• Another motivation is to reduce Eb/ N0 for a fixed BER
to reduce Tx power to reduce hardware cost
IMPLICATIONS OF CH CAP THEOREM

5. • Block Codes
Divide the message into blocks, each of k bits,
called datawords. Then add r redundant bit to
make length n=k+r
The resulting n-bit blocks are called
codewords.
• Convolution Codes
Absence of memory (nutshell- serial input no
blocks)
ERROR CORRECTION CODES

6. DEFINITIONS
• WORD:- Sequence of symbol.
• CODE :- Set of vectors called the codeword.
• HAMMING WEIGHT :- No of non-zero elements.
• HAMMING DISTANCE :- No of places the codeword differs.
D(c1, c2) = w(c1-c2)
• BLOCK LENGTH :- Length of code words in a BLOCK CODE,
denoted by “n”.
• MSG BITS :- “k”
• CODE RATE :- Of an (n,k) code , the ratio of (k/n), and reflects
the fraction of the codeword that consists the info.

7. • MINIMUM DISTANCE :- Minimum hamming
distance b/w any two codes.
• MINIMUM WEIGHT(w) :- The smallest weight of
any nonzero codeword.
DEFINITIONS

8. LINEAR CODES
• Properties
– Addition of two codewords gives third codeword.
– All zero code is also a codeword.
– Minimum distance = minimum weight.

9. LINEAR CODES
K- msg bits (m0, m1, m2, m3,…………… mk-1) b-parity bits (b0, b1, b2,
b3,…………… bn-k-1)
Codeword(c0, c1, c2, c3,…………… cn-1)
n – code length
Ci = bi (parity bit) i= 0,1,2,………n-k-1.
mi+k-n(msg bits) i= n-k, n-k+1, ……..n-1

10. • The (n-k) parity bits are linear sum of k msg bits.
• bi = p0i m0 + p1i m1 + ………….+ pk-1i mk-1
• Where the coeff are defined as follows:-
pij = 1 if bi depends on mj
0 otherwise
LINEAR CODES

11. Coefficient matrix P
p00 p01 …….. P0n-k-1
p10 p11 …….. P1,n-k-1
P = . . .
. . .
pk-1,0 pk-1,1 ……. Pk-1,n-k-1
Where pi = 0 or 1
Identity Matrix : Ik =
1 0 0 0…. 0
0 1 0 0…. 0
0 0 1 0…. 0
. . . .
. . . .
0 0 0 1 ….1

12.  All code words can be obtained as linear combination of
basis vectors.
 The basis vectors can be designated as {𝑔1, 𝑔2, 𝑔3,….., 𝑔 𝑘}
 For a linear code, there exists a k by n generator matrix such
that
𝑐1∗𝑛 = 𝑚1∗𝑘 . 𝐺 𝑘∗𝑛
where c={𝑐1, 𝑐2, ….., 𝑐 𝑛} and m={𝑚1, 𝑚2, ……., 𝑚 𝑘}
GENERATOR MATRIX

13. G = [ 𝐼 𝑘 P]
C = m.G = [m mP]
Message
part Parity part
m=(1110) and G = =
c= m.G = 𝒎 𝟏 𝒈 𝟏 + 𝒎 𝟐 𝒈 𝟐 + 𝒎 𝟑 𝒈 𝟑 + 𝒎 𝟒 𝒈 𝟒
= 1. 𝒈 𝟏 + 𝟏. 𝒈 𝟐 + 𝟏. 𝒈 𝟑 + 𝟎. 𝒈 𝟒
c = (1101000) + (0110100) + (1110010)
= (0101110)
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
𝒈 𝟎
𝒈 𝟏
𝒈 𝟐
𝒈 𝟑
Example:
Let us consider (7, 4) linear code where k=4 and n=7

14. • For decoding we require to separate the parity
bits and also find out if there was an error.
• We use a parity check matrix H s.t
H = [ PT I n-k ]
And H GT = 0
c HT = 0
Thus m c
c 0 null vector
GENERATOR
MATRIX
PARITY
CHECK
MATRIX T

15. CYCLIC CODES
• They form a sub class of linear block codes
• Properties
– Linearity a+b = c
– Cyclic property ie any cyclic shift of a code word is
also a code word.
BCH CODES ARE LINEAR CYCLIC BLOCK CODES

16. CHARACTERISTICS OF BCH CODES
• For positive pair of integers m≥3 and t, a (n, k) BCH
code has parameters:
– Block length: n = 2m – 1
– Number of check bits: n – k ≤ mt
– Minimum distance: dmin ≥ 2t + 1
• t<(2m – 1)/2 random errors detected and corrected.
• So also called ‘t-error correcting BCH code’.
• Major advantage is flexibility for block length and code
rate.
K- msg bits (m0, m1, m2, m3,…………… mk-1)
b-parity bits (b0, b1, b2,
b3,…………… bn-k-1)
n – code length

17. MANIFESTATION OF CHARACTERISTICS
• The parameters of some useful BCH codes are:
n = 2m – 1
n
n – k ≤ mt
k
t<(2m – 1)/2
t
Generator Polynomial
7 4 1 1 011
15 11 1 10 011
15 7 2 111 010 001
15 5 3 10 100 110 111
31 26 1 100 101
31 21 2 11 101 101 001
31 16 3 1 000 111 110 101 111
31 11 5 101 100 010 011 011 010 101
31 6 7 11 001 011 011 110 101 000 100
111

18. • Generator polynomial g(x)  specified in
terms of its roots from Galois Field GF(2k).
• g(x) has α,α2,…, α2t and their conjugates as its
roots.
• We choose g(x) from xn + 1 polynomial factors
by taking xn-k as highest term.
CHARACTERISTICS OF BCH CODES
Galois
Field
Root Elements Min Poly
Genr Poly

19. GALOIS FIELD
• Evariste Galois (1832)
Field +, -,
x, /
Ring
+, -
x
Gp
+, -

20. AXIOMS FOR FINITE FIELDS
1. Field F is closed under + and x iea+b and a.b are in F if a & b are in
F
2. Associative law : (a+b)+c = a+(b+c), a.(b.c) = (a.b).c
3. Commutative law : a+b=b+a, a.b=b.a
4. Distributive : a.(b+c)= a.b+a.c
5. Identity elements 1 & 0 must exist in F s.t
6. a+0 =a
7. a.1 = a
8. For any a there is additive inverse s.t a+(-a)=0
9. For any a except 0 there is multiplicative inverse (a= 𝑎−1
) s.t
a(𝑎−1) =1
10. A field with finite elements is called Galois Field denoted by
GF(q).
11. If 1st 8 properties are satisfied then its called a ring.

21. STRUCTURE OF FINITE FIELDS
• Gaolis Field : Fq ={0, α, α2, …, αq-1}.
• Primitive element : An element α in a finite field
Fq is called a primitive element (or generator) of
Fq if Fq ={0, α, α2, …, αq-1}.
For q = pm
• Where : q represents the number of elements in
the field.
p is a prime number
α is the primitive element
ord[α] = q-1 and αq-1 = 1
m is degree of primitive polynomial
• Now, π(α) is a primitive polynomial ϵ Fp [α] = 0
of degree m

22. • Example : Consider the field GF(5)=(0,1,2,3,4) , we will check if 2
and 3 are primitive elements
• 2 𝑜 = 1 (mod 5) = 1 3 𝑜 = 1 (mod 5) = 1
• 21 = 2 (mod 5) = 2 31 = 3 (mod 5) = 3
• 22 = 4 (mod 5) = 4 32 = 9 (mod 5) = 4
• 23 = 8 (mod 5) = 3 33 = 27 (mod 5) = 3

23. MODULAR ARITHMETIC
• Use only limited range of integers.
• We, define upper limit, called a ,modulus N.
• Then use only the integers 0 to N-1.
• This is modulo-N arithmetic.

24. Modulo-2 Arithmetic
Here modulus N is 2. we can use only 0
and 1. operation in this arithmetic are
very simple.
The addition and subtraction give the
same results. Here, we use XOR operation
for both the add and sub.
The result of an XOR operation is 0(if both
the bits are same. The result is 1 if the
any of the two bit is different.)

25. MODULO OPS
Mod 5 addition Mod 5 multiplication
for GF(5)

26. MIN POLY
• If βϵFqit is a root of xq -1 which is a poly with coeff in Fp[x]
• Min poly of β is : Mβ[x] = poly of least degree in Fp[x]
s.t Mβ[β] = 0 ie……
• Min poly is always monic.
• Mβ(x) = π(x− 𝜸)
𝜸𝛜conjugates of β = β,βp , βp2 ………..
Example of GF(16)
• Generator poly g(x)

27. • Message D: (0110011)
• Data: d(x)=x⁵+x⁴+x+1
• So code C(x)=d(x).g(x)
= (x⁵+x⁴+x+1)(x¹⁰+x⁹+x⁸+x⁶+x⁵+x³+1)
= x¹⁵+2x¹⁴+2x¹³+x¹²+2x¹¹+4x¹⁰+3x⁹+2x⁸
+2x⁷+2x⁶+2x⁵+2x⁴+x³+x+1
= x¹⁵+x¹²+ x⁹+ x³+x+1
• Codeword, C: (1001001000001011)

28. BLOCK DIAGRAM
Block diagram of (15,7) BCH Encoder
Mistake…..????