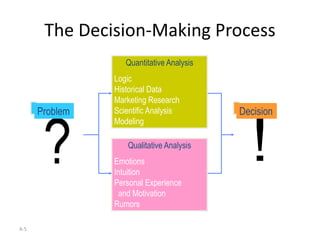
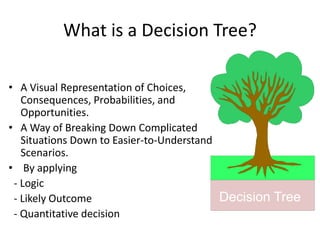
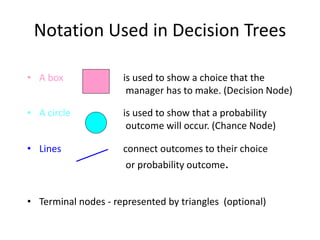
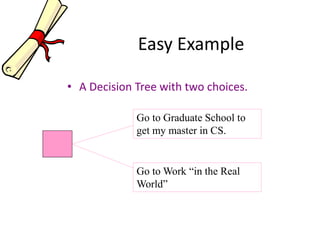
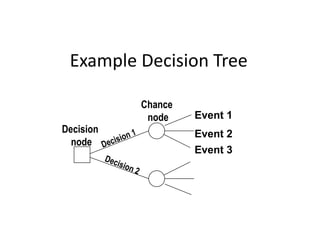
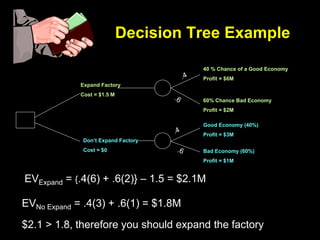
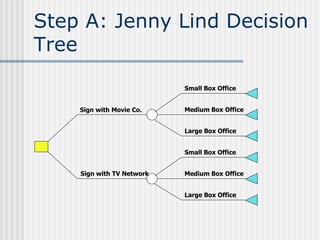
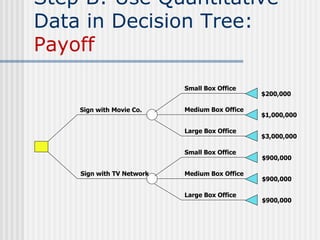
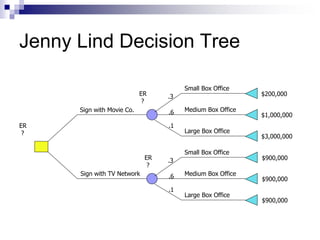
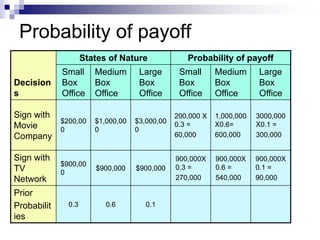
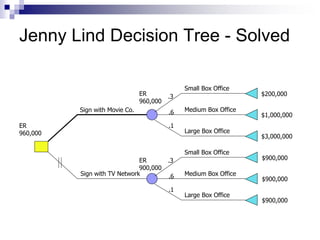
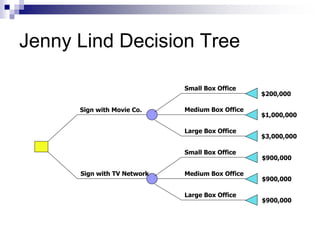
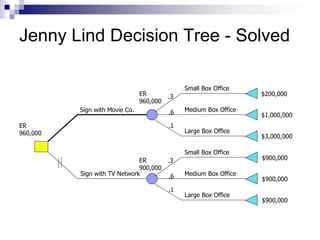
The document introduces decision trees as a quantitative tool for making decisions, detailing their structure, advantages, limitations, and practical applications. It provides examples, including scenarios involving expansion decisions in a factory and a writer considering contract options, illustrating how to calculate expected values for different outcomes. The document also touches on concepts like decision-making under uncertainty and the value of perfect information in optimizing decisions.

1. AN INTRODUCTION
TO
DECISION TREES:
widely used quantitative technique
to make decision

2. Duration: 30 minutes
Presented by
Fahim Muntaha

3. Objective/ Learning Outcome
• To have a clear idea about decision tree
• How to use this tool in making quantitative
decisions
• Impacts of these decisions in real life

4. Content
• Define Decision Tree
• Steps to make decision trees
• Limitations of Decision Tree
• Advantage of decision tree

5. A-5
The Decision-Making Process
Problem Decision
Quantitative Analysis
Logic
Historical Data
Marketing Research
Scientific Analysis
Modeling
Qualitative Analysis
Emotions
Intuition
Personal Experience
and Motivation
Rumors

6. Quantitative Decision Making Tools:
• Decision Trees,
• Payback Analysis &
• Simulations

7. What is a Decision Tree?
• A Visual Representation of Choices,
Consequences, Probabilities, and
Opportunities.
• A Way of Breaking Down Complicated
Situations Down to Easier-to-Understand
Scenarios.
• By applying
- Logic
- Likely Outcome
- Quantitative decision
Decision Tree

8. Notation Used in Decision Trees
• A box is used to show a choice that the
manager has to make. (Decision Node)
• A circle is used to show that a probability
outcome will occur. (Chance Node)
• Lines connect outcomes to their choice
or probability outcome.
• Terminal nodes - represented by triangles (optional)

9. Easy Example
• A Decision Tree with two choices.
Go to Graduate School to
get my master in CS.
Go to Work “in the Real
World”

10. Example Decision Tree
Decision
node
Chance
node Event 1
Event 2
Event 3

11. Decision Trees
 Solving the tree involves pruning all but the
best decisions at decision nodes, and finding
expected values of all possible states of
nature at chance nodes
 Works like a flow chart
 All paths - mutually exclusive

12. Mary’s Factory
Mary is the CEO of a gadget factory.
She is wondering whether or not it is a good idea to expand
her factory this year. The cost to expand her factory is $1.5M.
If she expands the factory, she expects to receive $6M if
economy is good and people continue to buy lots of gadgets,
and $2M if economy is bad.
If she does nothing and the economy stays good she expects
$3M in revenue; while only $1M if the economy is bad.
She also assumes that there is a 40% chance of a good
economy and a 60% chance of a bad economy.

13. Decision Tree Example
Expand Factory
Cost = $1.5 M
Don’t Expand Factory
Cost = $0
40 % Chance of a Good Economy
Profit = $6M
60% Chance Bad Economy
Profit = $2M
Good Economy (40%)
Profit = $3M
Bad Economy (60%)
Profit = $1M
EVExpand = {.4(6) + .6(2)} – 1.5 = $2.1M
EVNo Expand = .4(3) + .6(1) = $1.8M
$2.1 > 1.8, therefore you should expand the factory

14. Steps are
A. Draw the Diagram
B. Use quantitative data
i. Payoff Table and Probability
ii. Decision under uncertainty
iii. Expected Return
iv. Expected value of perfect
information

15. Problem: Jenny Lind
Jenny Lind is a writer of romance novels.
A movie company and a TV network both
want exclusive rights to one of her more
popular works. If she signs with the
network, she will receive a single lump
sum, but if she signs with the movie
company, the amount she will receive
depends on the market response to her
movie. What should she do?

16. Step A: Jenny Lind Decision
Tree
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network

17. Payouts and Probabilities
 Movie company Payouts
 Small box office - $200,000
 Medium box office - $1,000,000
 Large box office - $3,000,000
 TV Network Payout
 Flat rate - $900,000
 Probabilities
 P(Small Box Office) = 0.3
 P(Medium Box Office) = 0.6
 P(Large Box Office) = 0.1

18. Step B: Use Quantitative
Data in Decision Tree:
Payoff
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network
$200,000
$1,000,000
$3,000,000
$900,000
$900,000
$900,000

19. A-19
ii. Decision Making Under
Uncertainty - Criteria
 Maximax - Choose alternative that
maximizes the maximum outcome for
every alternative (Optimistic criterion).
 Maximin - Choose alternative that
maximizes the minimum outcome for
every alternative (Pessimistic criterion).
 Expected Value - Choose alternative with
the highest expected value.

20. Jenny Lind Decision Tree
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network
$200,000
$1,000,000
$3,000,000
$900,000
$900,000
$900,000
.3
.6
.1
.3
.6
.1
ER
?
ER
?
ER
?

21. Probability of payoff
Decision
s
States of Nature Probability of payoff
Small
Box
Office
Medium
Box
Office
Large
Box
Office
Small
Box
Office
Medium
Box
Office
Large
Box
Office
Sign with
Movie
Company
$200,00
0
$1,000,00
0
$3,000,00
0
200,000 X
0.3 =
60,000
1,000,000
X0.6=
600,000
3000,000
X0.1 =
300,000
Sign with
TV
Network
$900,00
0
$900,000 $900,000
900,000X
0.3 =
270,000
900,000X
0.6 =
540,000
900,000X
0.1 =
90,000
Prior
Probabilit
ies
0.3 0.6 0.1

22. A-22
Expected Value Equation
Probability of payoffEV A V P V
V P V V P V V P V
i i
i
i
N N
( ( )
( ) ( ) ( )
) =
=
 *
= * + * + + *
1
1 1 2 2
Number of states of nature
Value of Payoff
Alternative i
...
N

23. iii. Expected Return Criteria
EVmovie=0.3(200,000)+0.6(1,000,000)+0.1(3,000,000)
= $960,000 = EVBest
EVtv =0.3(900,000)+0.6(900,000)+0.1(900,000)
= $900,000
Select alternative with largest expected value
(EV).
Therefore, using this criteria, Jenny should select the
movie contract.

24. Jenny Lind Decision Tree - Solved
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network
$200,000
$1,000,000
$3,000,000
$900,000
$900,000
$900,000
.3
.6
.1
.3
.6
.1
ER
900,000
ER
960,000
ER
960,000

25. Something to Remember
Jenny’s decision is only going to be made one
time, and she will earn either $200,000,
$1,000,000 or $3,000,000 if she signs the movie
contract, not the calculated EV of $960,000!!
Nevertheless, this amount is useful for decision-
making, as it will maximize Jenny’s expected
returns in the long run if she continues to use this
approach.

26. A-26
iv. Expected Value of Perfect
Information (EVPI)
 EVPI places an upper bound on what
one would pay for additional information.
EVPI is the maximum you should pay to
learn the future.
 EVPI is the expected value under
certainty (EVUC) minus the maximum
EV.
EVPI = EVUC - maximum EV

27. Expected Value of Perfect Information
(EVPI)
What is the most that Jenny should
be willing to pay to learn what the size
of the box office will be before she
decides with whom to sign?

28. EVPI Calculation
EVwPI (or EVc)
=0.3(900,000)+0.6(1,000,000)+0.1(3,000,000) = $1,170,000
EVBest (calculated to be EVMovie from the previous page)
=0.3(200,000)+0.6(1,000,000)+0.1(3,000,000) = $960,000
EVPI = $1,170,000 - $960,000 = $210,000
Therefore, Jenny would be willing to spend up to
$210,000 to learn additional information before
making a decision.

29. Jenny Lind Decision Tree
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network
$200,000
$1,000,000
$3,000,000
$900,000
$900,000
$900,000

30. Jenny Lind Decision Tree - Solved
Small Box Office
Medium Box Office
Large Box Office
Small Box Office
Medium Box Office
Large Box Office
Sign with Movie Co.
Sign with TV Network
$200,000
$1,000,000
$3,000,000
$900,000
$900,000
$900,000
.3
.6
.1
.3
.6
.1
ER
900,000
ER
960,000
ER
960,000

31. Using Decision Trees
 Scientific analysis to decision making
 visual aids to structure
 solve sequential decision problems
 Especially beneficial when the complexity of the
problem grows
 Useful for operational decision making
 Encourage clear thinking and planning

32. Decision Tree Limitations
 local optimal solution not global optimal solution
 Possibility of duplication with the same sub-tree
on different paths
 Possibility of spurious relationships

33. Thanks