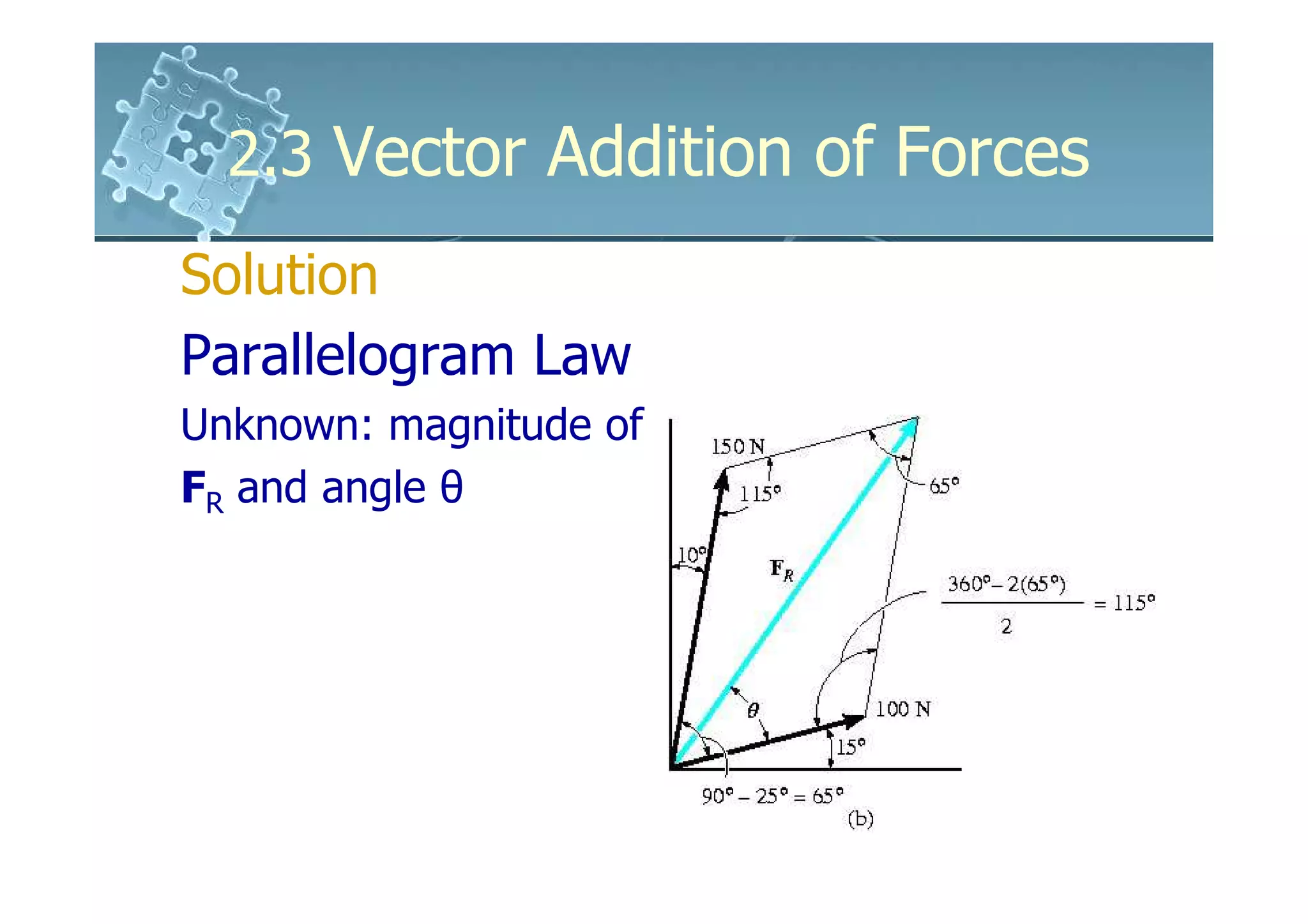
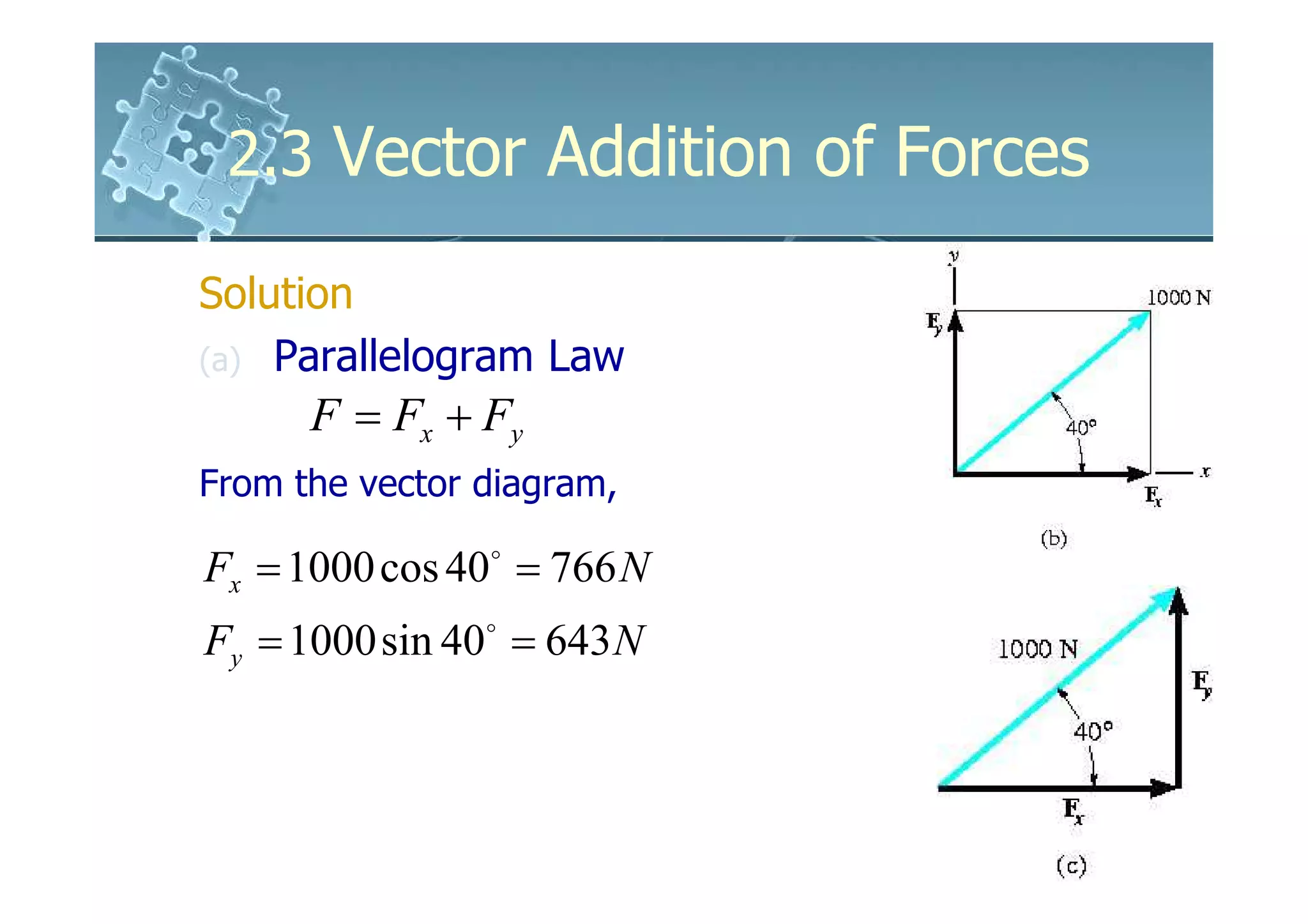
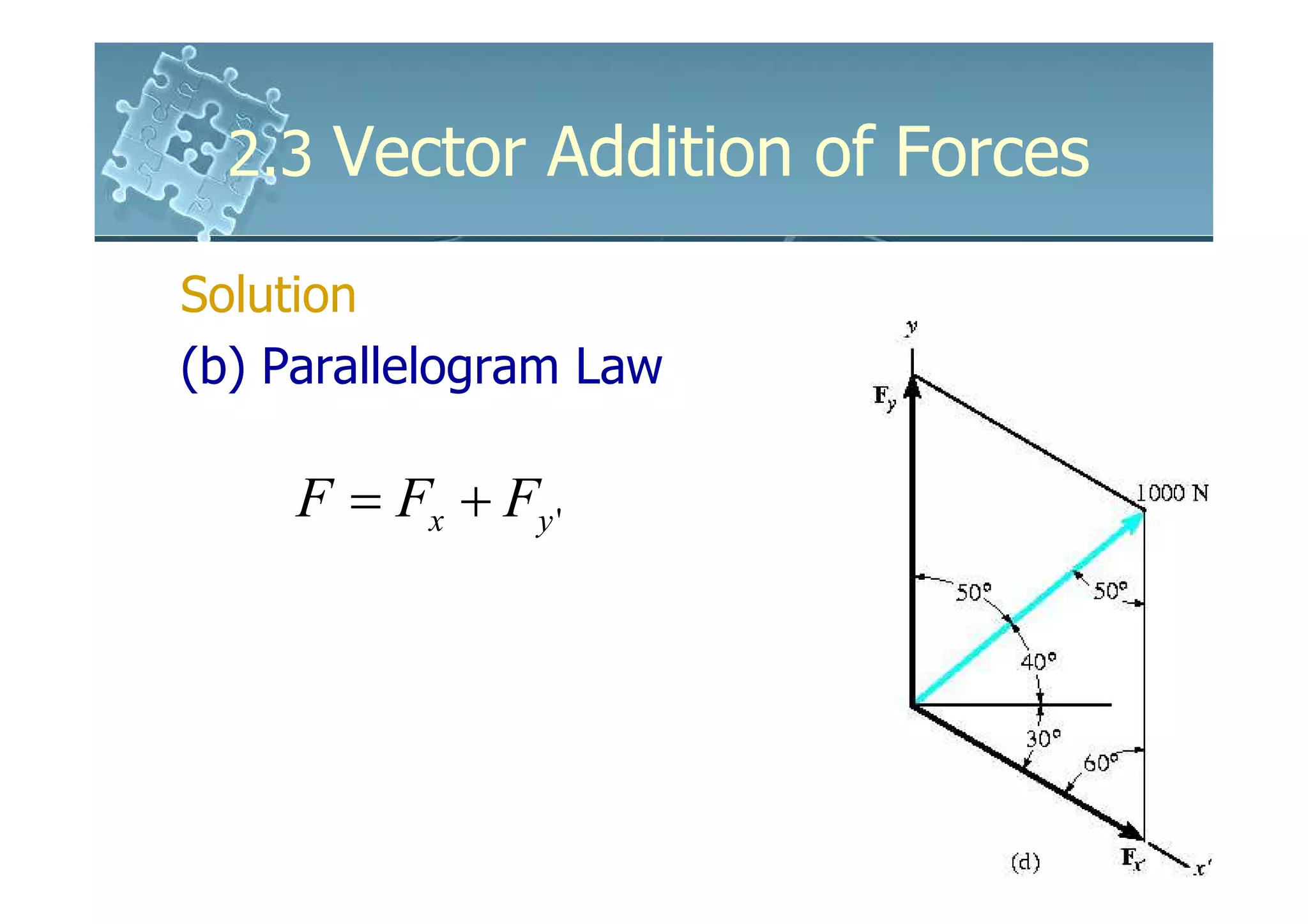
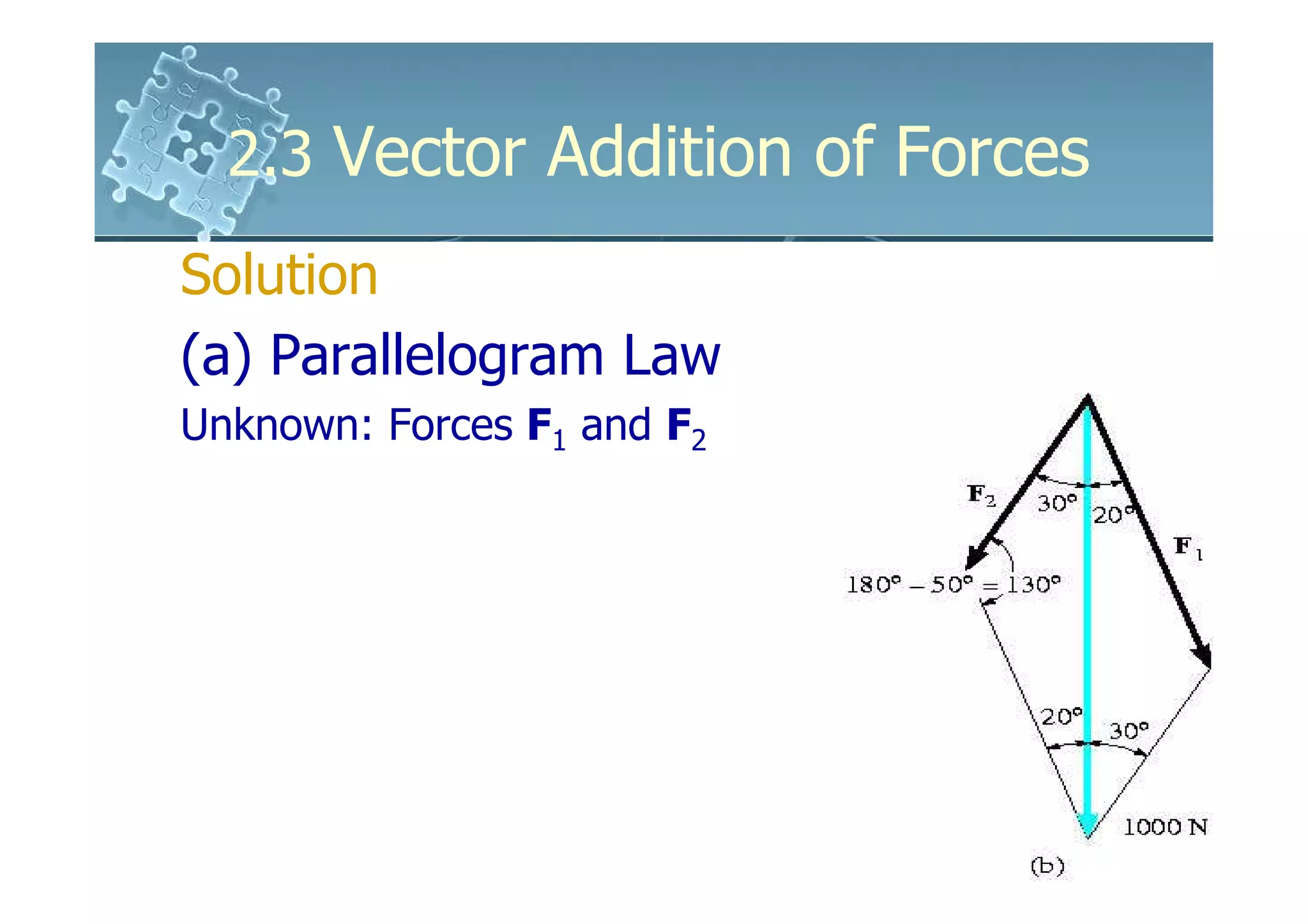
1) The document discusses vector addition of forces using the parallelogram law and trigonometry. 2) Forces can be added by constructing a parallelogram with the force vectors as sides and the resultant vector as the diagonal. 3) Trigonometric relationships like the law of sines and cosines allow determining the magnitudes and directions of resultant and component forces.

1. 2.3 Vector Addition of Forces
When two or more forces are added,
successive applications of the
parallelogram law is carried out to find the
resultant
Eg: Forces F1, F2 and F3 acts at a point O
- First, find resultant of
F1 + F2
- Resultant,
FR = ( F1 + F2 ) + F3

2. 2.3 Vector Addition of Forces
Example
Fa and Fb are forces exerting on the hook.
Resultant, Fc can be found using the
parallelogram law
Lines parallel to a and b
from the heads of Fa and Fb are
drawn to form a parallelogram
Similarly, given Fc, Fa and Fb
can be found

3. 2.3 Vector Addition of Forces
Procedure for Analysis
Parallelogram Law
- Make a sketch using the parallelogram law
- Two components forces add to form the
resultant force
- Resultant force is shown by the diagonal of the
parallelogram
- The components is shown by the sides of the
parallelogram

4. 2.3 Vector Addition of Forces
Procedure for Analysis
Parallelogram Law
To resolve a force into components along
two axes directed from the tail of the force
- Start at the head, constructing lines
parallel to the axes
- Label all the known and unknown force
magnitudes and angles
- Identify the two unknown components

5. 2.3 Vector Addition of Forces
Procedure for Analysis
Trigonometry
- Redraw half portion of the parallelogram
- Magnitude of the resultant force can be
determined by the law of cosines
- Direction if the resultant force can be
determined by the law of sines

6. 2.3 Vector Addition of Forces
Procedure for Analysis
Trigonometry
- Magnitude of the two components can be
determined by the law of sines

7. 2.3 Vector Addition of Forces
Example 2.1
The screw eye is subjected to two forces F1
and F2. Determine the
magnitude and direction
of the resultant force.

8. 2.3 Vector Addition of Forces
Solution
Parallelogram Law
Unknown: magnitude of
FR and angle θ

9. 2.3 Vector Addition of Forces
Solution
Trigonometry
Law of Cosines
FR = (100 N )2 + (150 N )2 − 2(100 N )(150 N ) cos115o
= 10000 + 22500 − 30000(− 0.4226 )
= 212.6 N
= 213 N

10. 2.3 Vector Addition of Forces
Solution
Trigonometry
Law of Sines
150 N 212.6 N
=
sin θ sin 115o
150 N
sin θ = (0.9063)
212.6 N
sin θ = 39.8o

11. 2.3 Vector Addition of Forces
Solution
Trigonometry
Direction Φ of FR measured from the horizontal
φ = 39.8 + 15
o o
= 54.8o ∠φ

12. 2.3 Vector Addition of Forces
Example 2.2
Resolve the 1000 N ( ≈ 100kg) force
acting on the pipe into the components in the
(a) x and y directions,
(b) and (b) x’ and y
directions.

13. 2.3 Vector Addition of Forces
Solution
(a) Parallelogram Law
F = Fx + Fy
From the vector diagram,
Fx = 1000 cos 40o = 766 N
Fy = 1000 sin 40o = 643 N

14. 2.3 Vector Addition of Forces
Solution
(b) Parallelogram Law
F = Fx + Fy '

15. 2.3 Vector Addition of Forces
Solution
(b) Law of Sines
Fx ' 1000 N
=
sin 50o sin 60o
 sin 50o 
Fx ' = 1000 N 
 sin 60o  = 884.6 N

 
Fy 1000 N
o
=
sin 70 sin 60o
 sin 70o 
Fy = 1000 N  sin 60o  = 1085 N

 
NOTE: A rough sketch drawn to scale will give some idea of the
relative magnitude of the components, as calculated here.

16. 2.3 Vector Addition of Forces
Example 2.3
The force F acting on the frame
has a magnitude of 500N and is
to be resolved into two components
acting along the members AB and
AC. Determine the angle θ,
measured below the horizontal,
so that components FAC is directed
from A towards C and has a
magnitude of 400N.

17. 2.3 Vector Addition of Forces
Solution
Parallelogram Law
500 N = FAB + FAC

18. 2.3 Vector Addition of Forces
Solution
Law of Sines
400 N 500 N
=
sin φ sin 60o
 400 N 
sin φ =   sin 60
o
 500 N 
sin φ = 0.6928
φ = 43.9o

19. 2.3 Vector Addition of Forces
Solution
Hence,
θ
θ = 180 − 60 − 43.9 = 76.1 ∠
o o o o
By Law of Cosines or
Law of Sines
Hence, show that FAB
has a magnitude of 561N

20. 2.3 Vector Addition of Forces
Solution
F can be directed at an angle θ above the horizontal
to produce the component FAC. Hence, show that
θ = 16.1° and FAB = 161N

21. 2.3 Vector Addition of Forces
Example 2.4
The ring is subjected to two forces
F1 and F2. If it is required that the
resultant force have a magnitude of
1kN and be directed vertically
downward, determine
(a) magnitude of F1 and F2
provided θ = 30°, and
(b) the magnitudes of F1 and F2 if
F2 is to be a minimum.

22. 2.3 Vector Addition of Forces
Solution
(a) Parallelogram Law
Unknown: Forces F1 and F2

23. 2.3 Vector Addition of Forces
Solution
Law of Sines
F1 1000 N
o
=
sin 30 sin 130o
F1 = 643N
F2 1000 N
o
=
sin 20 sin 130o
F2 = 446 N

24. 2.3 Vector Addition of Forces
Solution
(b) Minimum length of F2 occur
when its line of action is
perpendicular to F1. Hence
when
θ = 90o − 20o = 70o
F2 is a minimum

25. 2.3 Vector Addition of Forces
Solution
(b) From the vector
diagram
F1 = 1000 sin 70o N = 940 N
F2 = 1000 cos 70o N = 342 N