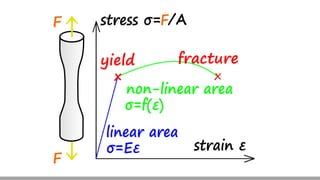
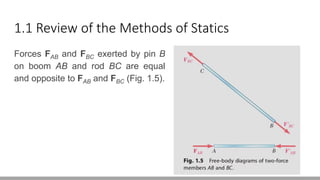
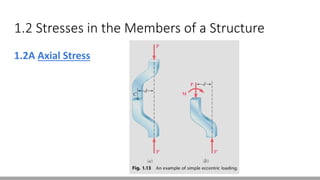
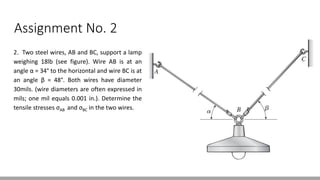
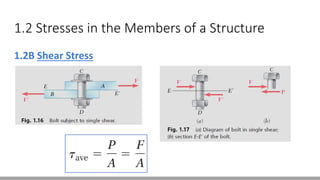
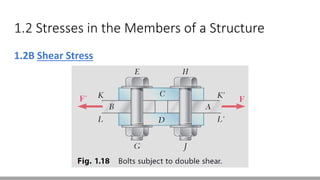
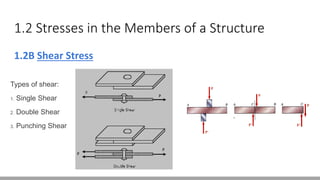
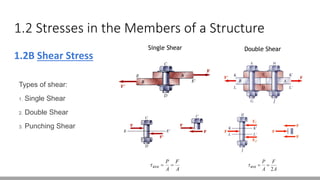
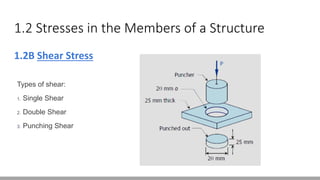
Here are the steps to solve this problem: (a) Given: Shear strength = 40 ksi Diameter of hole = 2.5 in Compressive stress limit in punch = 50 ksi Use the punching shear formula to find the maximum thickness: τ = P/A = 50 ksi A = πDh/4 Solve for h: h = 4P/(πDτ) = 4(50 ksi)/(π(2.5 in)(40 ksi)) = 0.625 in (b) Given: Thickness = 0.25 in Shear strength = 40 ksi Compressive stress limit = 50 ksi Use the

1. STRENGTH OF MATERIALS
Prepared by: Engr. Opalyn Seno
Teacher/Faculty: Br. Lambert Kwabla Azieve, SVD
Department of Civil Engineering
University of San Carlos

2. Objectives:
● The main objective of the study of the mechanics
of materials is to provide future
engineers/architects with the means of analyzing
and designing various machines and load-bearing
structures.
● Both the analysis and the design of a given
structure involve the determination of stresses
and deformations.

4. Introduction
Engineering Mechanics:
1. Statics (Rigid Bodies)
2. Dynamics (Movement of
Bodies)
3. Strength of Materials

5. Chapter 1: Introduction - CONCEPT OF STRESSES
● Stresses occur in all structures subject to loads. The first chapter
examines simple states of stress in elements, such as in the two-forced
members, bolts and pins in the structure.
Objectives
1. Review Statics needed to determine forces in members of simple structures.
2. Introduce concept of stress.
3. Define different stress types: axial normal stress, shearing stress and bearing stress.
4. Develop problem solving approach.
5. Discuss the components of stress on different planes and under different loading conditions.
6. Discuss main design considerations that needs review before preparing a design.

6. Introduction
The study of mechanics of materials provides
future engineers with the means of analyzing
and designing various machines and load-
bearing structures involving the
determination of stresses and deformations.
This first chapter is devoted to the concept of
stress.

7. 1.1 Review of the Methods of Statics
Consider the structure shown in Fig.
1.1, which was designed to support a
30-kN load. It consists of a boom AB
with a 30 x 50-mm rectangular cross
section and a rod BC with a 20-mm-
diameter circular cross section. These
are connected by a pin at B and are
supported by pins and brackets at A
and C, respectively.

8. 1.1 Review of the Methods of Statics
First draw a free-body diagram of
the structure by detaching it from its
supports at A and C and showing
the reactions that these supports
exert on the structure (Fig 1.2).

9. 1.1 Review of the Methods of Statics
Each of these reactions are represented by two components: Ax and Ay at A, and Cx
and Cy at C.

10. 1.1 Review of the Methods of Statics
We have found two of the four
unknowns, but cannot determine
the other two from these
equations, and no additional
independent equation can be
obtained from the free-body
diagram of the structure. We must
now dismember the structure.
Considering the free-body diagram
of the boom AB (Fig. 1.3).

11. 1.1 Review of the Methods of Statics
The following equilibrium equation:
Substituting for Ay from Eq. (1.4) into Eq. (1.3), we obtain Cy = +30 kN.
Expressing the results obtained for the reactions at A and C in vector
form, we have

12. 1.1 Review of the Methods of Statics
Since force FBC is directed along member BC, its slope is the same as
that of BC, namely, 3/4. We can, therefore, write the proportion
From which

13. 1.1 Review of the Methods of Statics
Forces FAB and FBC exerted by pin B
on boom AB and rod BC are equal
and opposite to FAB and FBC (Fig. 1.5).

14. 1.1 Review of the Methods of Statics
Passing a section at some arbitrary
point D of rod BC, we obtain two
portions BD and CD (Fig. 1.6).

15. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Actually, the internal force FBC represents the
resultant of elementary forces distributed
over the entire area A of the cross section
(Fig. 1.7). The average intensity of these
distributed forces is equal to the force per
unit area, FBC/A, on the section. Whether or
not the rod will break under the given loading
depends upon the ability of the material to
withstand the corresponding value FBC/A of
the intensity of the distributed internal forces.

16. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
The force per unit area, or intensity of the
forces distributed over a given section, is
called the stress and is denoted by the Greek
letter σ (sigma). The stress in a member of
cross-sectional area A subjected to an axial
load P is obtained by dividing the magnitude P
of the load by the area A:
Equation 1.5

17. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
A positive sign indicates a tensile stress (member in tension), and a
negative sign indicates a compressive stress (member in compression).
Units
When SI metric units are used, P is expressed in newtons (N) and A in square meters
(m2), so the stress σ will be expressed in N/m2. This unit is called a Pascal (Pa). How
ever, the pascal is an exceedingly small quantity and often multiples of this unit must
be used: the kilopascal (kPa), the megapascal (MPa), and the gigapascal (GPa).

18. Side Notes:
30kPa = 30kiloPascal = 30x103Pascal = 30x103 N/m2
30MPa = 30MegaPascal = 30x106Pascal = 30x106 N/m2
30GPa = 30GigaPascal = 30x109Pascal = 30x109 N/m2

19. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Units (SI) Units (US)
When U.S. customary units are used, force
P is usually expressed in pounds (lbs) or
kilopounds (kips), and the cross-sectional
area A is given in square inches (in2). The
stress σ then is expressed in pounds per
square inch (psi) or kilopounds per square
inch (ksi).

20. Side Notes:
30psi = 30pounds per square inch = STRESS IN US UNITS
30ksi = 30kilopounds per square inch = 30x103 pounds per square inch
STRESS IN US UNITS
Force = pounds (lbs) / kilopounds (kips) = x103 pounds
A = squared inch = in2

21. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress

22. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.1
Considering the structure of Fig. 1.1, assume that
rod BC is made of a steel with a maximum
allowable stress σall = 165 MPa. Can rod BC
safely support the load to which it will be
subjected? The magnitude of the force FBC in the
rod was 50 kN. Recalling that the diameter of the
rod is 20 mm, use Eq. (1.5) to determine the
stress created in the rod by the given loading.

23. Side Notes:
σall = stress allowable = the allowed stress that the material could
take
σ = stress actual / actual stress given by the force of the material
σ< or =σall
stress actual < stress allowable
or
stress actual = stress allowable

24. Side Notes:
Steps in solving Axial Stress:
1. Determine all the given. (P, A, σ)
2. Determine the requirement of the problem. (P, A, σ)
3. Solve using the formula.
4. Conclusion. (Therefore, the ....)

25. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.1

26. Side Notes:
20mm = 0.02m or 20x10-3
1m = 1000mm

27. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.2
As an example of design, let us return to the
structure of Fig. 1.1 and assume that aluminum
with an allowable stress σall = 100 MPa is to be
used. Since the force in rod BC is still P = FBC =
50 kN under the given loading, from Eq. (1.5).
What is the diameter of rod BC given the
allowable stress?

28. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.2

29. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.3
A hollow steel tube with an inside diameter of
100mm must carry a tensile load of 400kN.
Determine the outside diameter of the tube if the
stress is limited to 120 MN/m2.

30. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.3
A hollow steel tube with an inside diameter of
100mm must carry a tensile load of 400kN.
Determine the outside diameter of the tube if the
stress is limited to 120 MN/m2.

31. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.3
A hollow steel tube with an inside diameter of
100mm must carry a tensile load of 400kN.
Determine the outside diameter of the tube if the
stress is limited to 120 MN/m2.

32. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.3
Determine the largest weight W that can be
supported by two wires shown. The stress in
either wire is not to exceed 30 ksi. The cross-
sectional areas of wires AB and AC are 0.4 in2
and 0.5 in2, respectively.

33. 1.2 Stresses in the Members of a Structure
1.2A Axial Stress
Concept Application 1.3
Required: Largest weight (w)
Draw the free-body diagram (FBD)

34. Assignment No. 1
1. A solid circular post ABC (see figure) supports a load P1 = 2500lb
acting at the top. A second load P2 is uniformly distributed aroung the
shelf at B. The diameters of the upper and lower parts of the post are
dAB = 1.25 in. and dBC = 2.25 in., respectively.
(a) Calculate the normal stress σAB in the upper part of the post.
(b) If it is desired that the lower part of the post have the same
compressive stress as the upper part, what would be the
magnitude of the load P2?

35. Solution:

36. Assignment No. 2
2. Two steel wires, AB and BC, support a lamp
weighing 18lb (see figure). Wire AB is at an
angle α = 34° to the horizontal and wire BC is at
an angle β = 48°. Both wires have diameter
30mils. (wire diameters are often expressed in
mils; one mil equals 0.001 in.). Determine the
tensile stresses σAB and σBC in the two wires.

37. Solution:

39. Units to Remember (Recall)
UNIT OF STRESS (S.I.)
Force: N, kN, MN
Area: m2, cm2, mm2
Stress: N/m2 = Pa (Pascal)
kN/m2 = kPa (kilopascal)
MN/m2 = MPa (MegaPascal) = MPa
Force: lb, kips
Area: ft2, in2
Stress: lb/in2 = psi
lb/ft2 = psf 1kip = 1000lb; 2kips = 2000lbs;
ksi = 1 kip/in2 (1000lb/in2) ; ex: 8ksi = 8000psi
psf = lb/ft2 (pound per square foot)
UNIT OF STRESS (US Customary)

40. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
A very different type of stress is obtained when
transverse forces P and P9 are applied to a
member AB (Fig. 1.14).

41. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Passing a section at C between the points of
application of the two forces (Fig. 1.15a), you
obtain the diagram of portion AC shown in Fig.
1.15b.

42. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Internal forces must exist in the plane of the
section, and their resultant is equal to P. These
elementary internal forces are called shearing
forces, and the magnitude P of their resultant is
the shear in the section. Dividing the shear P by
the area A of the cross section, you obtain the
average shearing stress in the section. Denoting
the shearing stress by the Greek letter ꚍ (tau).

43. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress

44. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Note: The value obtained is an average value of the shearing stress over the entire section.
Contrary to what was said earlier for normal stresses, the distribution of shearing stresses
across the section cannot be assumed to be uniform. As you will see in Chap. 6, the actual
value ꚍ of the shearing stress varies from zero at the surface of the member to a maximum
value ꚍmax that may be much larger than the average value ꚍave.

45. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress

46. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress

47. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
For example, if splice plates C and D are used to
connect plates A and B (Fig. 1.18), shear will take
place in bolt HJ in each of the two planes KK' and
LL' (and similarly in bolt EG). The bolts are said to
be in double shear.

48. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
To determine the average shearing stress in each
plane, draw free-body diagrams of bolt HJ and of
the portion of the bolt located between the two
planes (Fig. 1.19). Observing that the shear P in
each of the sections is P = F/2, the average
shearing stress is:

49. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Types of shear:
1. Single Shear
2. Double Shear
3. Punching Shear

50. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Types of shear:
1. Single Shear
2. Double Shear
3. Punching Shear
Single Shear Double Shear

51. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Types of shear:
1. Single Shear
2. Double Shear
3. Punching Shear

52. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Concept Application 1.1
What force is required
to punch a 20-mm
diameter hole in a plate
that is 25 mm thick?
The shear strength is
350 MN/m2.

53. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Concept Application 1.2
A hole is to be punched out of a plate having a
shearing strength of 40 ksi. The compressive
stress in the punch is limited to 50 ksi. (a)
Compute the maximum thickness of plate in
which a hole 2.5 inches in diameter can be
punched. (b) If the plate is 0.25 inch thick,
determine the diameter of the smallest hole that
can be punched.

54. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Concept Application 1.2
A hole is to be punched out of a plate having a
shearing strength of 40 ksi. The compressive
stress in the punch is limited to 50 ksi. (a)
Compute the maximum thickness of plate in
which a hole 2.5 inches in diameter can be
punched. (b) If the plate is 0.25 inch thick,
determine the diameter of the smallest hole
that can be punched.

55. 1.2 Stresses in the Members of a Structure
1.2B Shear Stress
Concept Application 1.2
A hole is to be punched out of a plate having a
shearing strength of 40 ksi. The compressive
stress in the punch is limited to 50 ksi. (a)
Compute the maximum thickness of plate in
which a hole 2.5 inches in diameter can be
punched. (b) If the plate is 0.25 inch thick,
determine the diameter of the smallest hole
that can be punched.

56. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress in Connections
Bolts, pins, and rivets create stresses in the
members they connect along the bearing surface
or surface of contact.
Bearing Stress is the contact pressure between
separate bodies.
For example, consider again the two plates A and
B connected by a bolt CD that were discussed in
the preceding section (Fig. 1.16).

57. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress in Connections
The bolt exerts on plate A a force P equal and
opposite to the force F exerted by the plate on the
bolt (Fig. 1.20). The force P represents the
resultant of elementary forces distributed on the
inside surface of a half- cylinder of diameter d and
of length t equal to the thickness of the plate.

58. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress in Connections
Since the distribution of these forces—and of the
corresponding stresses—is quite complicated, in
practice one uses an average nominal value sb of
the stress, called the bearing stress, which is
obtained by dividing the load P by the area of the
rectangle representing the projection of the bolt
on the plate section (Fig. 1.21).

59. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress in Connections
where t is the plate thickness and d the diameter
of the bolt, we have
The difficulty inherent in a variable stress
distribution is avoided by the common
practice of assuming the bearing stress to be
uniformly distributed over a reduced area
equal to the projected area of the rivet hole.

60. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress in Connections
Other examples:
1. Soil pressure beneath piers.
2. Forces on the bearing plates.
3. Between a rivet or bolt and the
contact surface of the plate.

61. 1.2 Stresses in the Members of a Structure
1.2C Bearing Stress
Concept Application 1.1
In the figure, assume that a 20-mm-diameter
rivet joins the plates that are each 110 mm
wide. The allowable stresses are 120 MPa for
bearing in the plate material and 60 MPa for
shearing of rivet. Determine (a) the minimum
thickness of each plate; and (b) the largest
average tensile stress in the plates.

62. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress
Concept Application 1.1
In the figure, assume that a 20-mm-diameter
rivet joins the plates that are each 110 mm
wide. The allowable stresses are 120 MPa for
bearing in the plate material and 60 MPa for
shearing of rivet. Determine (a) the minimum
thickness of each plate; and (b) the largest
average tensile stress in the plates.

63. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress
Concept Application 1.1
In the figure, assume that a 20-mm-diameter
rivet joins the plates that are each 110 mm
wide. The allowable stresses are 120 MPa for
bearing in the plate material and 60 MPa for
shearing of rivet. Determine (a) the minimum
thickness of each plate; and (b) the largest
average tensile stress in the plates.

64. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress
Concept Application 1.2
The lap joint shown in the figure below is fastened by
four ¾-in.-diameter rivets. Calculate the maximum safe
load P that can be applied if the shearing stress in the
rivets is limited to 14 ksi and the bearing stress in the
plates is limited to 18 ksi. Assume the applied load is
uniformly distributed among the four rivets.

65. 1.2 Stresses in the Members of a Structure
1.2B Bearing Stress
Concept Application 1.2
The lap joint shown in the figure below is fastened by
four ¾-in.-diameter rivets. Calculate the maximum safe
load P that can be applied if the shearing stress in the
rivets is limited to 14 ksi and the bearing stress in the
plates is limited to 18 ksi. Assume the applied load is
uniformly distributed among the four rivets.

66. Assignment No. 2
1. Three steel plates, each 16mm thick, are joined by
two 20-mm diameter rivets as shown in the figure.
a. If the load P=50kN, what is the largest bearing stress
acting on the rivets?
b. If the ultimate shear stress for the rivets is 180MPa,
what force Pult is required to cause the rivets to fail in
shear?
(Disregard friction between the plates.)

67. Solution:

68. Assignment No. 2
2. The connection shown in the figure consists of five
steel plates, each 3/16 in. thick, joined by a single 1/4
in. diameter bolt. The total load transferred between
the plates is 1200lb, distributed among the plates as
shown.
a.) Calculate the largest shear stress in the bolt,
disregarding friction between the plates.
b.) Calculate the largest bearing stress acting against
the bolt.

69. Solution:

70. More Examples (Axial Stress):
1. A rod is composed of an aluminum section
rigidly attached between steel and bronze
sections, as shown in the figure. Axial loads
are applied at the positions indicated. If P =
3000 lb and the cross sectional area of the rod
is 0.5 in2, determine the stress in each
section.

71. More Examples (Axial Stress):
2. An aluminum rod is rigidly attached
between a steel rod and a bronze rod as
shown. Axial loads are applied at the
positions indicated. Find the maximum
value of P that will not exceed a stress in
steel of 140 MPa, in aluminum of 90 MPa,
or in bronze of 100 MPa.

72. More Examples (Shear and Bearing Stress):
1. The lap joint is connected by three 20-
mm-diameter rivets. Assuming that the
axial load P = 50 kN is distributed equally
among the three rivets, find (a) the shear
stress in a rivet; (b) the bearing stress
between a plate and a rivet; and (c) the
maximum average tensile stress in each
plate.
Ans: (a) 53.1 MPa; (b)
33.3 MPa; (c) 18.18 MPa

73. References
1. Mechanics of Materials 7th Edition by Beer, Johnston, DeWolf and
Mazurek
2. Strength of Materials 4th Edition by Pytel and Singer
3. Mechanics of Materials by Pytel and Kiusalaas (2nd Edition)