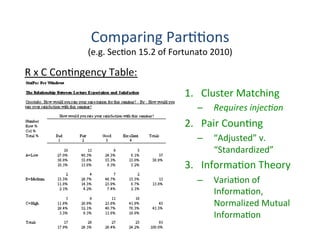
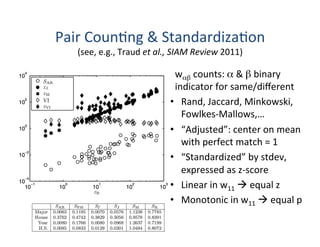
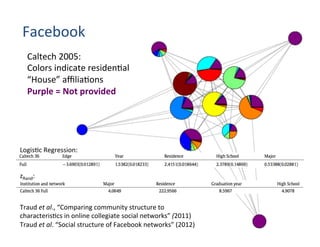
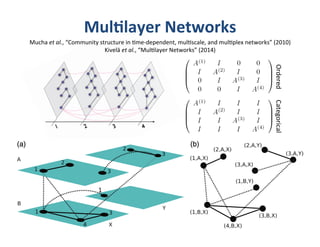
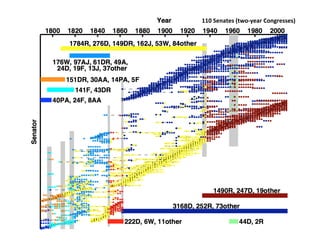
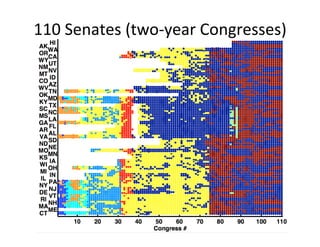
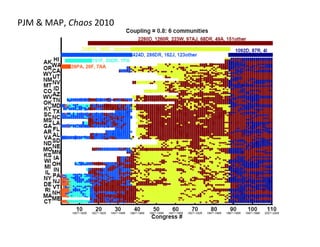
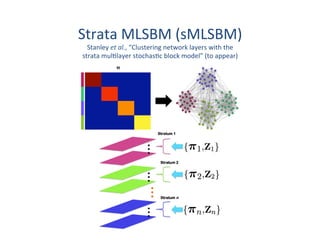
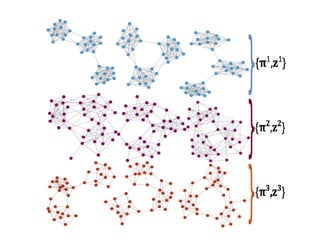
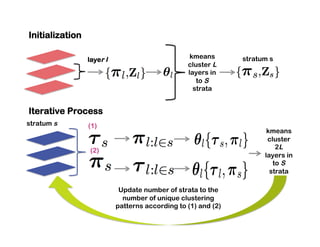
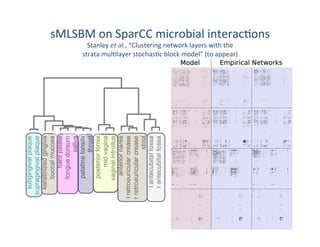
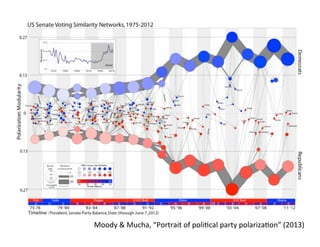
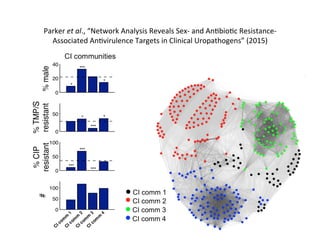
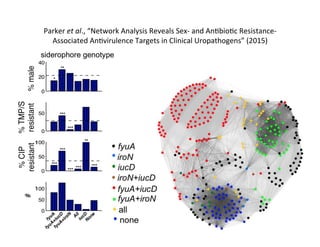
This document presents a talk on detecting communities in networks. It begins with an introduction to the concept of communities and their usefulness in network analysis. It then discusses two main approaches to calculating communities - descriptive methods like modularity, and generative methods like stochastic block models. The talk concludes by considering future directions for community detection research. Throughout, it acknowledges limitations and cites influential papers in the field.














![Community
Detec'on:
Null
Model
&
Computa'onal
Heuris'cs
• GOAL:
Assign
nodes
to
communi'es
in
order
to
maximize
quality
func'on
Q
• NP-‐Complete
[Brandes
et
al.
2008]
~
enumerate
possible
par''ons
• Numerous
packages
developed/developing
– e.g.
igraph
library
(R,
python),
NetworkX
– Need
appropriate
null
model](https://image.slidesharecdn.com/05dukesnhworkshopcommunities-160930145709-170629181102/85/05-Communities-in-Networks-2016-22-320.jpg)



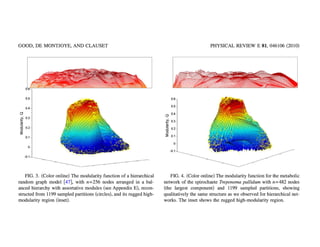
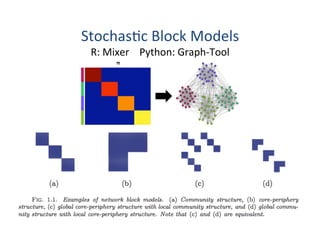
![Poli'cal
Blogs
(Adamic
&
Glance,
WWW-‐2005)
“On
closer
inspec0on,
we
find
that
the
method
[(a)]
fails
in
this
case
because
it
does
not
take
into
account
the
wide
varia0on
among
the
degrees
of
nodes
in
the
network.
In
this
network
(and
many
others)
degrees
vary
over
a
great
range,
whereas
degrees
in
the
block
model
are
Poisson
distributed
and
narrowly
peaked
about
their
mean.
This
means,
in
effect,
that
there
is
no
choice
of
parameters
for
the
model
that
gives
a
good
fit
to
the
data.
Ficng
this
block
model
is
similar
to
ficng
a
straight
line
through
an
inherently
curved
set
of
data
points—you
can
do
it,
but
it
is
unlikely
to
give
you
a
meaningful
answer.”
—Newman,
Nature
Physics
2012
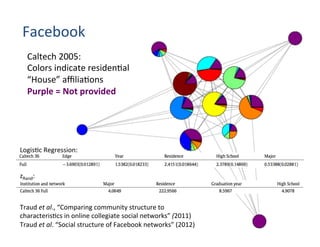
Similar
visualiza'ons
from
different
models
in
Amini
et
al.,
arXiv
(2012)
Bo[om
Right:
Par''ons
v.
overlap
&
extrac'on
(Wilson
et
al.
in
prep)](https://image.slidesharecdn.com/05dukesnhworkshopcommunities-160930145709-170629181102/85/05-Communities-in-Networks-2016-26-320.jpg)


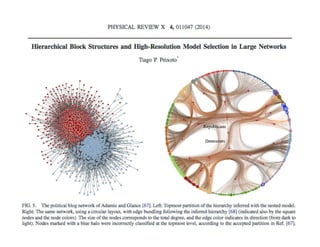
![At
the
most
general
level…
Two
related
but
different
issues
to
keep
straight:
1. Theore'cal
Concept
(e.g.,
“Modularity”,
“Map
Equa'on”,
“Stochas'c
Block
Models”)
2. Computa'onal
Heuris'c
&
Implementa'on
(e.g.
“Fast
Greedy”,
“Louvain”,
“Itera've
Improvement”,
or
the
specific
SBM
code
[possible
ini'aliza'on
issues
with
some])
And,
finally,
how
do
you
compare
communi'es?](https://image.slidesharecdn.com/05dukesnhworkshopcommunities-160930145709-170629181102/85/05-Communities-in-Networks-2016-37-320.jpg)