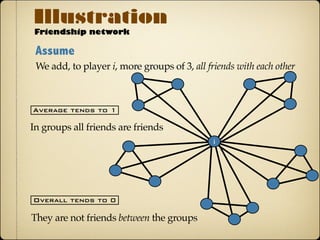
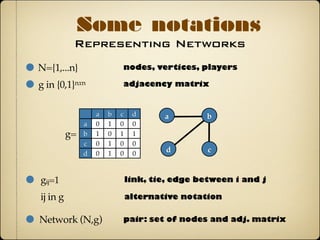
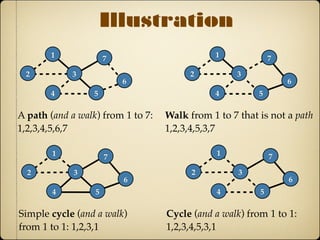
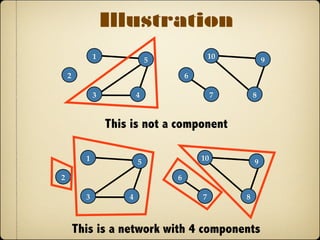
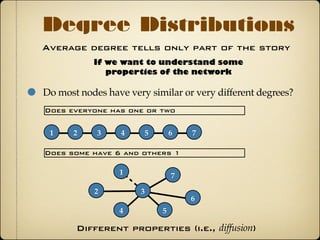
This document provides an overview of social networks and their structure. It discusses how social networks form and influence individual behavior. Key concepts introduced include: - Nodes represent individuals and links represent relationships between nodes in a social network. - Basic network properties like degree, neighborhood, paths, and components help describe network structure. - Real-world networks tend to have short path lengths and exhibit clustering, degree distributions, and transitivity. - Understanding network structure can provide insights into how behaviors and outcomes spread through social ties.

1. Social Networks & Structure
Block 4

2. This block comprises the remaining
second part of the course
Aim Block 4
To understand
The emergence of social networks & their
consequences for individual behavior and well-being
How do networks emerge (form)?
How do networks influence behavior?

3. Lecture 8
B a c k g r o u n d &
F u n d a m e n t a l s o f
Social Networks

4. Lecture 8
Aim Lecture 8
To learn
Basic ways of navigating through a network
How to represent networks
Some elements of the structure of a network
Nodes, links...
Walks, paths, cycles...
Components, Neighborhoods, clustering

5. Network Studies
Social Networks
People’s relationships show patterns
SOCIAL NETWORKS
These social networks affect people’s lives considerably

6. Social Networks
Examples
Western industrialized countries
Marsden & Gorman, 2001
Between 1/3 & 2/3 of the working population
found their job through informal social ties
Chances of illness, recovery or dying
Partly depend on people’s network
House, Landis & Umberson, 1988
Participation in political protest
Affected by friendship and family networks
Opp & Gern, 1993

7. study networks
Many disciplines
Sociology
In the course we will look at networks in which
Phone networks - Email networks - Marriages -
Friendships - co-authorships - collaborations
Decision-making people are the nodes
Economics
Computer Science
Statistical Physics
Mathematics (graphs theory)
Relationships between different
people, organizations, countries

8. Example
Facebook - Friendship relations
Mary
Ana Tom
Link between two people indicates they are friends (relationship)
Ana is friends with Tom & Mary
Centrality - How many paths does a person have between others
If Mary & Tom want to meet they need to go through Ana
Ana lies in the shortest path between Tom & Mary
Popularity

9. There are different kinds
Patterns in Networks
Global patterns
How are the different connectedness of individuals distributed
in the society (people well connected, or not)?
How long does it take me to reach one person from another
(path lengths)?
Segregation patterns
If people have different characteristics (types), do we see
separation between them?

10. There are different kinds
Patterns in Networks
Local patterns
Do we see tight clusters of people connected to each other?
Positions in networks
How influential is somebody in the network (centrality)?
Are my friends friends between each other (transitivity)?
We will be looking at networks overall & also
zooming-in to the individuals
Macro and Micro levels

11. Representing Networks
Some notations
N={1,...n}
gij=1
nodes, vertices, players
g in {0,1}nxn adjacency matrix
a b c d
a
b
c
d
0 1 0 0
1 0 1 1
0 1 0 0
0 1 0 0
a b
cd
link, tie, edge between i and j
ij in g alternative notation
Network (N,g) pair: set of nodes and adj. matrix
g=

12. Ways of navigating through a network
Basic Definitions
A walk from i1 to ik: a sequence of nodes (i1, i2,...,ik) and a
sequence of links (i1i2,i2i3,...,ik-1ik) such that ik-1ik in g for each k
A sequence of links that take you
from the first node to the last node
A path is a walk (i1, i2,...,ik) with each node ik distinct
A cycle is a walk where i1 = ik
A geodesic is a shortest path between two nodes
Represented by its nodes (i1, i2,...,ik)

13. Illustration
1
2 3
4 5
6
7
A path (and a walk) from 1 to 7:
1,2,3,4,5,6,7
1
2 3
4 5
6
7
Walk from 1 to 7 that is not a path
1,2,3,4,5,3,7
1
2 3
4 5
6
7
Simple cycle (and a walk)
from 1 to 1: 1,2,3,1
1
2 3
4 5
6
7
Cycle (and a walk) from 1 to 1:
1,2,3,4,5,3,1

14. walks, paths, cycles
Importance
will help us understand
Centrality
Diffusion
Transmission of information

15. Subgraphs that make up the network
Components
Connectivity
A network (N,g) is connected if there is a path between every
two nodes
I can reach any node from any other node
Component
A maximally connected subgraph
- (N’,g’) is a subset of (N,g)
- (N’,g’) is connected
- i in N’ and ij in g, implies j in N’ and ij in g’
Most social networks(even large) have the property
that a large portion of nodes are connected

16. Illustration
Is this a component?
1
2
3 4
5 10
6
7 8
9
Is the subset of nodes {3,4,5} and links {3-4,4-5,5-3}
maximally connected?
Can we find any player connected to either of the
nodes in the subset {3,4,5} who is not in our
selected “component”?

17. Illustration
This is not a component: player 1 is left out
1
2
3 4
5 10
6
7 8
9
What are the components in this network?

18. Illustration
This is not a component: player 1 is left out
1
2
3 4
5 10
6
7 8
9
1
2
3 4
5 10
6
7 8
9
This is a network with 4 components

19. Tend to have short path lengths
Real life networks
We connect a large number of nodes
using fairly small number of links
Milgram (1967) - Experiment
Ask people to send letters from one part of the US to another
I have to send a letter to John
Smith, who lives in Massachusetts,
who is a lawyer, and I live in
Nebraska
Send the letter to someone you know, tell them to send them
to somebody they know, and so forth...
The intent is reaching the person the letter is sent to

20. Findings
Milgram (1967) - How many steps?
Median 5 for the 25% of the letters that made it
Quite small - consider you start from an individual to reach
another, in the other side of the country, without knowing her
Coauthorship studies - Reaching one author from another
Grossman (1999) Math: mean 7.6, max 27
Newman (2001) Physics: mean 5.9, max 20
Goyal et al. (2004) Economics: mean 9.5, max 29
WWW - Reaching one page from another
Adamik & Pitkow (1999): mean 3.1 (in 85% of 50 million possible
pages
Facebook - Reaching one person from another
Backstrom et al. (2012): mean 4.74 (721 million users)

21. Definitions
Neighborhood & Degree
The neighborhood of a node i: Ni(g)={j|ij in g}
The set of other nodes that i is linked to in g
The degree of a node i: di=#Ni(g)
Count how many neighbors i has in g
Basic ideas that will be very important
along the rest of the course

22. Average degree tells only part of the story
Degree Distributions
Do most nodes have very similar or very different degrees?
Does everyone has one or two
If we want to understand some
properties of the network
1 2 3 4 5 6 7
Does some have 6 and others 1
1
2 3
4 5
6
7
Different properties (i.e., diffusion)

23. What fraction of my friends
are friends with each other
Clustering
Take a given node i i
k
j
Choose two neighbors j and k
What is the chance that j and k are friends?
What is the frequency of links among the friends of i?
Clustering of i: Cli(g)=#{kj in g|k,j in Ni(g)}/#{kj|k,j in Ni(g)}
Fraction: How many pairs of my friends are connected
to each other divided by every pair of friends I have
Average Clustering: Mean of all the individual clusterings
Overall Clustering: Aggregate of all the individual clusterings

24. Illustration
i
Average tends to 1
Overall tends to 0
Friendship network
In groups all friends are friends
They are not friends between the groups
Assume
We add, to player i, more groups of 3, all friends with each other

25. My friends are friends
Transitivity
i
k
j
Tendency towards transitivity
The existence of two links ij in g and jk in g often makes
it more likely that also the link ik in g exists:
prob(ik|ij,jk in g) > prob(ik in g|ij in g and ik not in g)
Observed in many real-life networks:
If people link because they share common attributes (i.e., race),
transitivity is one of the consequences. (Simmel, 1908)
In networks of inter-firm alliances transitivity is common, for it
helps reduce risk of opportunistic behavior by sharing common
partners (Gulati, 1998)

26. Checklist
Many relationships are networked
i
k
j
Understanding network structure can help us
understand behavior & outcomes
Networks are complex
But can be partly described by some characteristics
- Degree distribution
- Clustering
In the next lecture we will check
network characteristics & behavior

27. Questions?