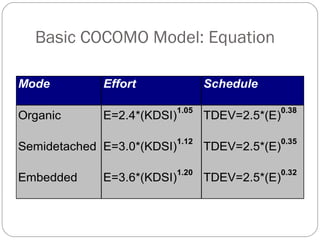
The COCOMO model is a widely used software cost estimation model developed by Barry Boehm in 1981. It predicts effort, schedule, and staffing needs based on project size and characteristics. The Basic COCOMO model uses three development modes (Organic, Semidetached, Embedded) and a simple formula to estimate effort and schedule based on thousands of delivered source instructions. However, its accuracy is limited as it does not account for various project attributes known to influence costs. Function Point Analysis is an alternative size measurement that counts different types of system functions and complexity factors to estimate effort and cost.

1. COCOMO Model
Basic

2. Introduction
COCOMO is one of the most widely used software
estimation models in the world
It was developed by Barry Boehm in 1981
COCOMO predicts the effort and schedule for a software
product development based on inputs relating to the size of
the software and a number of cost drivers that affect
productivity

3. COCOMO Models
COCOMO has three different models that reflect the
complexity:
the Basic Model
the Intermediate Model
and the Detailed Model

4. The Development Modes: Project
Characteristics
Organic Mode
• Relatively small, simple software projects
• Small teams with good application experience work to a
set of less than rigid requirements
• Similar to the previously developed projects
• relatively small and requires little innovation
Semidetached Mode
• Intermediate (in size and complexity) software projects in
which teams with mixed experience levels must meet a mix
of rigid and less than rigid requirements.

5. Contd…
Embedded Mode
• Software projects that must be developed within a set of tight
hardware, software, and operational constraints.

6. COCOMO:
Some Assumptions
Primary cost driver is the number of Delivered Source
Instructions (DSI) / Delivered Line Of Code
developed by the project
COCOMO estimates assume that the project will enjoy
good management by both the developer and the
customer
Assumes the requirements specification is not
substantially changed after the plans and requirements
phase

7. Basic COCOMO
Basic COCOMO is good for quick, early, rough order of
magnitude estimates of software costs
It does not account for differences in hardware
constraints, personnel quality and experience, use of
modern tools and techniques, and other project attributes
known to have a significant influence on software costs,
which limits its accuracy

8. Basic COCOMO Model: Formula
E=ab (KLOC or KDSI) b
b
D=cb(E) d
b
P=E/D
where E is the effort applied in person-months, D is the
development time in chronological months, KLOC / KDSI
is the estimated number of delivered lines of code for the
project (expressed in thousands), and P is the number of
people required. The coefficients ab, bb, cb and db are given in
next slide.

9. Contd…
Software project ab bb cb db
Organic 2.4 1.05 2.5 0.38
Semi-detached 3.0 1.12 2.5 0.35
Embedded 3.6 1.20 2.5 0.32

10. Basic COCOMO Model: Equation
Mode Effort Schedule
Organic E=2.4*(KDSI)
1.05
TDEV=2.5*(E)
0.38
Semidetached E=3.0*(KDSI)
1.12
TDEV=2.5*(E)
0.35
Embedded E=3.6*(KDSI)
1.20
TDEV=2.5*(E)
0.32

11. Basic COCOMO Model: Limitation
Its accuracy is necessarily limited because of its lack of
factors which have a significant influence on software costs
The Basic COCOMO estimates are within a factor of 1.3
only 29% of the time, and within a factor of 2 only 60% of
the time

12. Basic COCOMO Model: Example
 We have determined our project fits the characteristics of Semi-Detached
mode
 We estimate our project will have 32,000 Delivered Source Instructions.
Using the formulas, we can estimate:
 Effort = 3.0*(32) 1.12
= 146 man-months
 Schedule = 2.5*(146) 0.35
= 14 months
 Productivity = 32,000 DSI / 146 MM
= 219 DSI/MM
 Average Staffing = 146 MM /14 months
= 10 FSP

13. Function Point Analysis
What is Function Point Analysis (FPA)?
 It is designed to estimate and measure the time, and thereby the cost, of
developing new software applications and maintaining existing software
applications.
 It is also useful in comparing and highlighting opportunities for productivity
improvements in software development.
 It was developed by A.J. Albrecht of the IBM Corporation in the early 1980s.
 The main other approach used for measuring the size, and therefore the time
required, of software project is lines of code (LOC) – which has a number of
inherent problems.

14. Function Point Analysis
How is Function Point Analysis done?
Working from the project design specifications, the following
system functions are measured (counted):
 Inputs
 Outputs
 Files
 Inquires
 Interfaces

15. Function Point Analysis
These function-point counts are then weighed (multiplied) by
their degree of complexity:
Simple Average Complex
Inputs 2 4 6
Outputs 3 5 7
Files 5 10 15
Inquires 2 4 6
Interfaces 4 7 10

16. Function Point Analysis
A simple example:
inputs
3 simple X 2 = 6
4 average X 4 = 16
1 complex X 6 = 6
outputs
6 average X 5 = 30
2 complex X 7 = 14
files
5 complex X 15 = 75
inquiries
8 average X 4 = 32
interfaces
3 average X 7 = 21
4 complex X 10 = 40
Unadjusted function points 240

17. Function Point Analysis
In addition to these individually weighted function points, there are factors that affect
the project and/or system as a whole. There are a number (~35) of these factors
that affect the size of the project effort, and each is ranked from “0”- no influence to
“5”- essential.
The following are some examples of these factors:
 Is high performance critical?
 Is the internal processing complex?
 Is the system to be used in multiple sites and/or by multiple organizations?
 Is the code designed to be reusable?
 Is the processing to be distributed?
 and so forth . . .

18. Function Point Analysis
Continuing our example . . .
Complex internal processing = 3
Code to be reusable = 2
High performance = 4
Multiple sites = 3
Distributed processing = 5
Project adjustment factor = 17
Adjustment calculation:
Adjusted FP = Unadjusted FP X [0.65 + (adjustment factor X 0.01)]
= 240 X [0.65 + ( 17 X 0.01)]
= 240 X [0.82]
= 197 Adjusted function points

19. Function Point Analysis
But how long will the project take and how much will it cost?
As previously measured, programmers in our organization
average 18 function points per month. Thus . . .
197 FP divided by 18 = 11 man-months
If the average programmer is paid $5,200 per month
(including benefits), then the [labor] cost of the project will
be . . .
11 man-months X $5,200 = $57,200

20. Function Point Analysis
Because function point analysis is independent of language used,
development platform, etc. it can be used to identify the
productivity benefits of . . .
One programming language over another
One development platform over another
One development methodology over another
One programming department over another
Before-and-after gains in investing in programmer training
And so forth . . .

21. Function Point Analysis
But there are problems and criticisms:
 Function point counts are affected by project size
 Difficult to apply to massively distributed systems or to systems with very
complex internal processing
 Difficult to define logical files from physical files
 The validity of the weights that Albrecht established – and the consistency
of their application – has been challenged
 Different companies will calculate function points slightly different, making
intercompany comparisons questionable