The document discusses the properties and behavior of diprotic acids, focusing primarily on carbonic acid and its dissociation steps. It details the interrelations between species, mass balance, and equilibrium constants, alongside the calculation of equivalence points in various scenarios. It emphasizes the importance of concentration and ionization fractions in determining pH levels and equilibrium across aqueous solutions.

1. Diprotic Acids
Tableaux & Equivalence Points
aqion.de
updated 2017-04-15

2. monoprotic acid: HA
diprotic acid: H2A
triprotic acid: H3A
our focus
most prominent representative:
carbonic acid (with A-2 =CO3
-2)

3. pure H2O
OH-
H+
H2O + H2A
H2A
HA-
A-2
OH-
H+
acid H2A
5species
2 components

4. Acid H2A
(Concepts & Notation)
Part 1

5. Two Dissociation Steps
H2A ⇄ H+ + HA- ⇄ 2H+ + A-2
Five Species (NS = 5)
H+, OH-, H2A, HA-, A-2

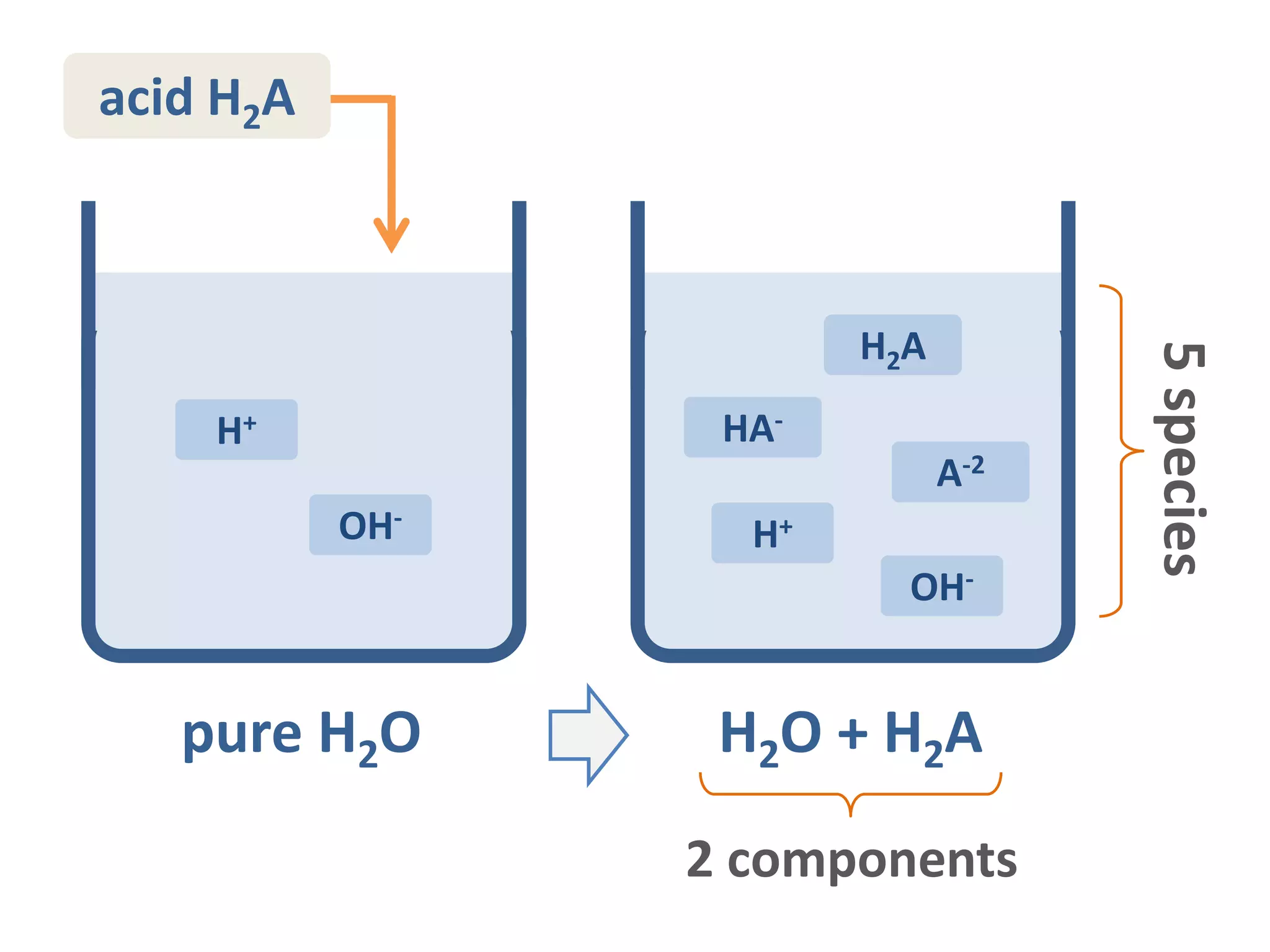
6. (1) Species are interrelated by
conservation rules:
H+ OH- H2A HA- A-2
charge balance
massbalance
[H2A]+[HA-]+[A-2]=CT
[H+] – [OH-] – [HA-] – 2[A-2] = 0
total amount of acid

7. (2) Species are interrelated by
Mass-Action Laws:
H2A = H+ + HA- HA- = H+ + A-2
H2O = H+ + OH- Kw = {H+
}{OH-
}
K1 = {H+
}{HA-
}/{H2A}
H+ OH- H2A HA- A-2
K2 = {H+
}{A-2
}/{HA-
}
EquilibriumReactions
self-ionization of water

8. H+ OH- H2A HA- A-2
Kw = {H+} {OH-} = 10-14
K1 = {H+} {HA-} / {H2A} (1st diss. step)
K2 = {H+} {A-2} / {HA-} (2nd diss. step)
CT = [H2A] + [HA-] + [A-2] (mass balance)
0 = [H+] – [HA-] – 2[A-2] – [OH-] (charge balance)
5 species (unknowns)  5 equations
{..} = activities, [..] = molar concentrations

9. Replace: Activities {..}  Concentrations [..]
Kw = [H+] [OH-]
K1 = [H+] [HA-] / [H2A]
K2 = [H+] [A-2] / [HA-]
CT = [H2A] + [HA-] + [A-2]
0 = [H+] – [HA-] – 2[A-2] – [OH-]
This is valid for small ionic strengths (I0) or apparent equilibrium constants.
Ionization Fractions (a0, a1, a2)
exact relation between pH and CT

10. Ionization Fractions
a0 = [1 + K1/x + K1K2/x2]-1 [H2A] = CT a0
a1 = [x/K1 + 1 + K2/x]-1 [HA-] = CT a1
a2 = [x2/(K1K2) + x/K2 + 1]-1 [A-2] = CT a2
x = [H+] = 10-pH
K1 = 10-6.35
K2 = 10-10.33
carbonic acid
mass balance
a0 + a1 + a2 = 1
pK1 pK2

11. Exact Relations between pH and CT
4th order equation in x = [H+] = 10-pH
0 = x4 + K1x3 + {K1K2– CTK1– Kw} x2
– K1 {2CTK2 + Kw} x – K1K2Kw
x/K21
x/K1K/x
x
K
xC
2
21w
T









total amount CT (of acid H2A) for a given pH
measured quantities

12. x/K21
x/K1K/x
x
K
xC
2
21w
T









constraint: CT  0
CT  (x – Kw/x)
x2  Kw x  Kw
1/2 x  10-7 pH  7
(pure water: CT = 0  pH = 7)

13. Remark:
Don’t confuse CT with [H2A]
CT > [H2A]
total amount of acid H2A
that enters the solution:
CT = [H2A] + [HA-] + [A-2]
amount of
aqueous species H2A(aq)
(dissolved,
but non-dissociated)(measured quantity)

14. Generalization
(Acids, Ampholytes, Bases)
Part 2

15. NS = NC + NR
number of
species
number of
equilibrium
reactions
number of
components
(master species)

16. C1 C2 ...
s1 11 12
s2 21 22
s3 31 32
...
Tableaux Method
TOT C1 = 11 s1 + 21 s2 + 31 s3 + ...
NSNC matrix
of stoichiometric
coefficientsNC components
NSspecies
s2 = 21 C1 + 22 C2 + ...

17. C1 C2 ...
s1 11 12 K1
s2 21 22 K2
s3 31 32 K3
...
Tableaux Method
{C1}21 {C2}21 / {s2} = K2
NC components
NSspecies
s2 = 21 C1 + 22 C2 + ...
equilibrium
constants
mass-action law

18. Example: pure H2A solution
choice is arbitrary
(H+ should be included)
H+
H2A
NC = 2
A set of NC components
defines a basis in the
„vector space“ of chemical species.

19. H+ H2A
H+ 1
OH- -1 -Kw
H2A 1
HA- -1 1 -K1
A-2 -2 1 -K1K2
H2A 0 1
pure H2A solution (NS = 5, NC = 2)
TOT H = [H+] – [HA-] – 2[A-2] – [OH-] = 0
chargebalance=protonbalance

20. Generalization
BnH2-n A
B+ = Na+, K+, NH4
+
n = 0 acid
n = 1 ampholyte
n = 2 base
H2A
BHA
B2A

21. A clever choice of components
simplifies the calculations:
n C1 C2
0 H2A H+ H2A
1 BHA H+ HA-
2 B2A H+ A-2
also called
Proton Reference Level (PRL)

22. H+ H2A B+
H+ 1
OH- -1 -Kw
H2A 1
HA- -1 1 -K1
A-2 -2 1 -K1K2
B+ 0
H2A 0 1 0
pure H2A solution
TOT H = [H+] – [HA-] – 2[A-2] – [OH-] = 0
n=0

23. H+ HA- B+
H+ 1
OH- -1 -Kw
H2A 1 1 K1
HA- 1
A-2 -1 1 -K2
B+ 1
BHA 0 1 1
pure BHA (or HA-) solution
TOT H = [H+] + [H2A] – [A-2] – [OH-] = 0
n=1

24. H+ A-2 B+
H+ 1
OH- -1 -Kw
H2A 2 1 K1K2
HA- 1 1 K2
A-2 1
B+ 2
B2A 0 1 2
pure B2A (or A-2) solution
TOT H = [H+] + 2[H2A] + [HA-] – [OH-] = 0
n=2

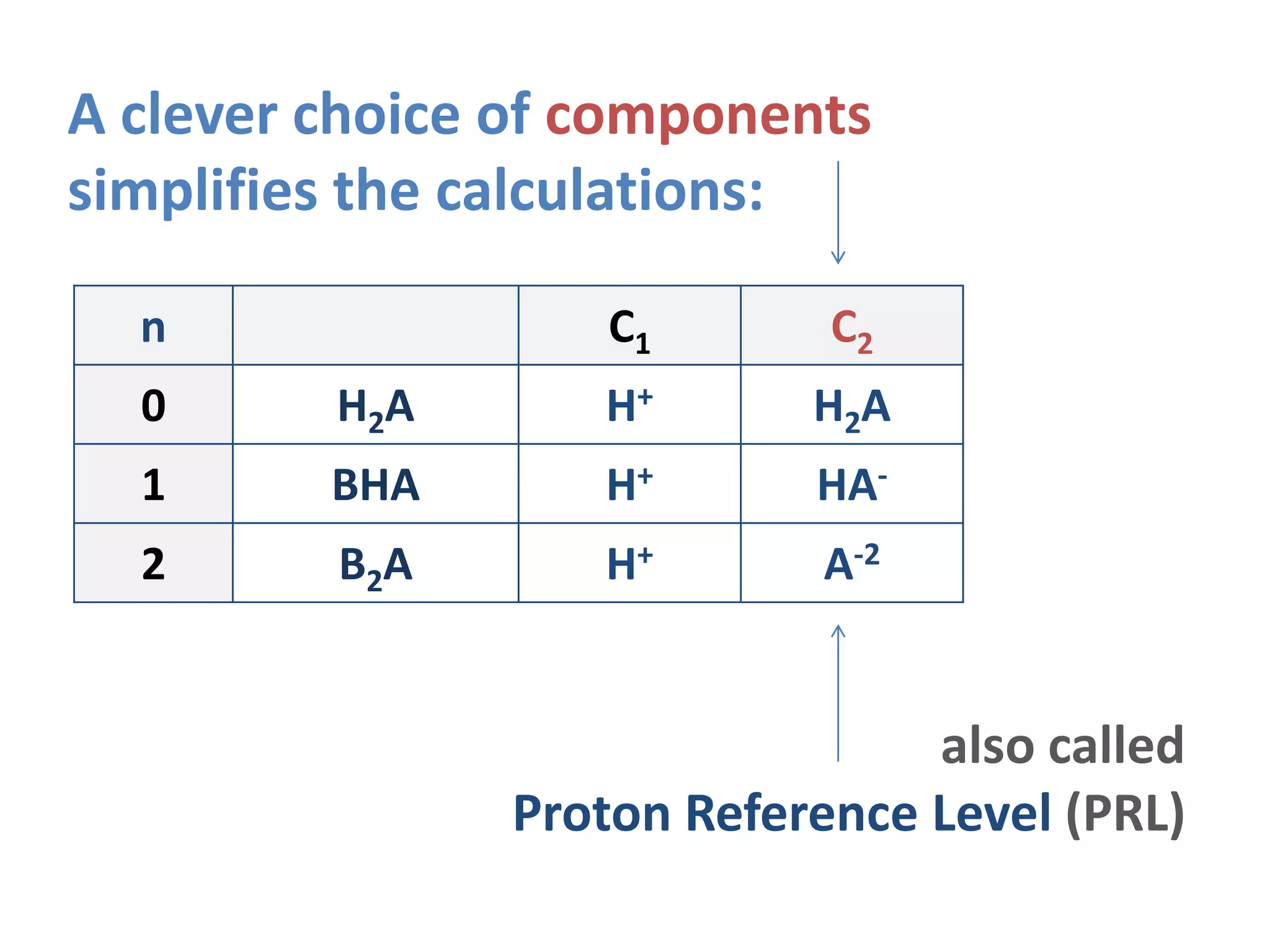
25. H+ H2-nA-n B+ n=0 n=1 n=2
H+ 1
OH- -1 -Kw -Kw -Kw
H2A n 1 1 K1 K1K2
HA- n-1 1 -K1 1 K2
A-2 n-2 1 -K1K2 -K2 1
B+ n
BnH2-nA 0 1 n
General Case: pure BnH2-nA solution
TOT H = [H+] – [OH-] + n[H2A]
+ (n-1)[HA-] + (n-2)[A-2] = 0

26. Kw = {H+} {OH-} = 10-14
K1 = {H+} {HA-} / {H2A} (1st diss. step)
K2 = {H+} {A-2} / {HA-} (2nd diss. step)
CT = [H2A] + [HA-] + [A-2] (mass balance)
0 = [H+] + n[H2A] + (n-1)[HA-] + (n-2)[A-2] – [OH-]
General Case: pure BnH2-nA solution
(proton balance)
Set of 5 equations

27. only for n=0:
proton balance = charge balance
The general case (BnH2-nA) differs from the
pure acid case (H2A) by the proton balance only
TOT H = [H+] + n[H2A] + (n-1)[HA-] + (n-2)[A-2] – [OH-] = 0
[H+] – [HA-] – 2[A-2] – [OH-] = 0
Proton Balance

28. Set of 5 equations
replace activities {..} by concentrations [..]
(or K by conditional equilibrium constants cK)
closed-form 4th order equation in x=[H+]
0 = x4 + {K1+ nCT} x3
+ {K1K2+ (n-1)CTK1– Kw} x2
+ K1 {(n-2)CTK2– Kw} x – K1K2Kw
exact relation between CT and pH=-log x

29. C
C
convert 4th-order equation to CT
12
12w
T
K/x)n0()n1(x/K)n2(
K/x1x/K
x
K
xC









total amount of BnH2-nA
as a function of pH = – log x
1
21
2w
T n
x/KK/x1
x/K21
x
K
xC


















30. Ionization Fractions
a0 = [1 + K1/x + K1K2/x2]-1 [H2A] = CT a0
a1 = [x/K1 + 1 + K2/x]-1 [HA-] = CT a1
a2 = [x2/(K1K2) + x/K2 + 1]-1 [A-2] = CT a2
x = [H+] = 10-pH
are independent of n
(same for pure H2A, HBA, B2A solutions)

31. Equivalence Points
(of Carbonic Acid & Co)
Part 3

32. Equivalence Points (EP)
n=0 pH of pure H2A solution: [H+] = [HA-]
n=1 pH of pure BHA solution: [H2A] = [A-2]
n=2 pH of pure B2A solution: [HA-] = [OH-]
amount
of acid
amount
of base=

33. Carbonic Acid & Co
pH of pure H2CO3 solution: [H+] = [HCO3
-]
pH of pure NaHCO3 solution: [H2CO3] = [CO3
-2]
pH of pure Na2CO3 solution: [HCO3
-] = [OH-]
Equivalence
Points
pK1 = -log K1 6.35
pK2 = -log K2 10.33
pKw = -log Kw 14.0

34. Calculation of
Equivalence Points
1 from Ionization Fractions (a0, a1, a2)
2 from
1
21
2w
T n
x/KK/x1
x/K21
x
K
xC

















3 numerical model (e.g. PhreeqC)
(incl. activity corrections)
exact
approximation

35. x = [H+] = 10-pH
EP based on Ionization Fractions
[H+] = [HA-]  x = CT a1  CT = x2/K1 + x + K2
[H2A] = [A-2]  a0 = a2  x2 = K1K2 (independent of CT)
[HA-] = [OH-]  CT a1 = Kw/x  CT = (Kw/x2)(x2/K1 + x + K2)
pH = -log x
CT[M]
[H+] = [HA-]
[H2A] = [A-2]
[HA-] = [OH-]
Example: Carbonic Acid
This is an
approximation
and fails
for CT  10-7 M.
1
outside range
of applicability
self-ionization
of H2O is ignored

36. pH
CT[M]
H2CO3
NaHCO3
Na2CO3
n= 0
n=1
n=2
)pH(fn
x/KK/x1
x/K21
x
K
xC n
1
21
2w
T 
















Equivalence Points (EP) based on2
n = 0 H2CO3
n = 1 NaHCO3
n = 2 Na2CO3

37. versus
EP based on
ionization fractions
(approximate)
Equivalence Points (exact)
1
pH
CT[M]
H2CO3
NaHCO3
Na2CO3
n=0
n=1
n=2
2
dashed lines
)pH(fn
x/KK/x1
x/K21
x
K
xC n
1
21
2w
T 

















38. Equivalence
Points (EP)
pH
CT[M]
H2CO3
NaHCO3
Na2CO3
I = 0 seawater
pK1 6.35 6.00
pK2 10.33 9.10
pKw 14.0 13.9
dashed: seawater
conditional (apparent)
equilibrium constants at 25 °C
[Millero 1995]
2

39. pH
CT[M]
H2CO3 NaHCO3
Na2CO3
 activity corrections
 NaHCO3 and NaCO3
- species
3
lines: xlogpHwithn
x/KK/x1
x/K21
x
K
xC
1
21
2w
T 
















2
dots: PhreeqC calculations with:
3 EP based on
Numerical
Model

40. Summary of Assumptions
done in previous EP Calculations
approach
self-ionization
of water
activity
corrections
formation of
complexes (e.g.
NaHCO3
-)
no no no
yes no no
yes yes yes
1
2
3
determines behavior
at very low CT
determines behavior
at very high CT
(especially for Na2CO3)

41. CT = 10-4 M
CT = 10-3 M
[H+] = [HCO3
-] [HCO3
-] = [OH-]
Equivalence
Points (EP)
as intersection points
EP
pH at
CT = 10-4 M
pH at
CT = 10-3 M
H2CO3 5.16 4.68
Na2CO3 9.86 10.52
plots based on PhreeqC or aqion calculations
demonstrated for two total
concentrations CT:

42. www.aqion.de/site/122 (EN)
www.aqion.de/site/59 (DE)
Ref
www.aqion.de/file/acid-base-systems.pdf