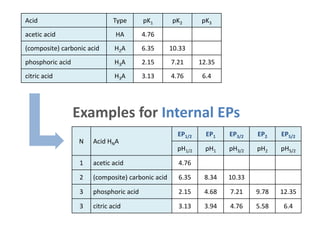
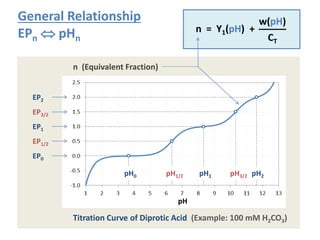
The document provides a comprehensive overview of equivalence points in acid-base systems, detailing the classification and systematics of equivalence and semi-equivalence points for n-protic acids. It elaborates on the concepts of acid-base pairs, different species in diprotic and triprotic acids, and the mathematical relationships governing their titration. The general approach offers a framework for understanding acid behavior in terms of equivalent fractions and pH, emphasizing the role of concentration and acidity constants.

1. Equivalence Points (EP)
Systematics & Classification
aqion.de
updated 2017-09-28

2. The set of Equivalence Points
(EP & semi-EP) is the unique barcode
of an acid-base system.
Motivation
- 2 -

3. An Equivalence Point is a special
equilibrium state at which chemical
equivalent quantities of acids and bases
are mixed:
EP: [acid] = [base]
square brackets indicate
molar concentrations
Common Definition
- 3 -

4. This definition will be extended to
N-protic acid systems in two ways:
Part 1
Simplified Approach General Approach
Part 2
simple & nice equations
(but without self-ionization
of H2O)
based on integer and
half-integer values of
equivalent fraction n = CB /CT
- 4 -

5. Simplified Approach
(valid for High-Concentrated Acids)
Part 1

6. The Simplified Approach
is based on the equivalence of
acid species concentrations.
more precisely:
conjugated pairs of acid species
What is a conjugated acid-base pair?
- 6 -

7. acid
(proton donor)
conj. base
(proton acceptor)
conjugate pair
HA = H+ + A-
- 7 -

8. HA + H2O = A- + H3O+
conjugate pair
conjugate pair
acid base conj. base conj. acid
- 8 -

9. Diprotic Acid
H2A = H+ + HA-
HA- = H+ + A-2
conj. acid base
acid conj. base
1st dissociation step:
2nd dissociation step:
HA- is the conj. base of acid H2A, and
HA- is the conj. acid of base A-2
- 9 -

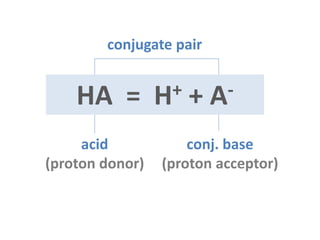
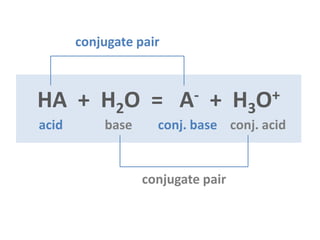
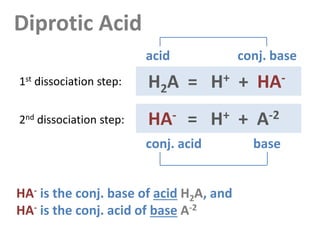
10. HA- is the conj. base of acid H2A, and
HA- is the conj. acid of base A-2
EP of HA-: [H2A] = [A-2]
Diprotic Acid
Notation:
The diprotic acid has 3 species: [H2A], [HA-] and [A-2].
They add up to the total amount: CT = [H2A] + [HA-] + [A-2]  [H2A]T

11. Triprotic Acid (H3A)
EP of H2A-: [H3A] = [HA-2]
EP of HA-2: [HA-2] = [A-3]
In addition, there are much more types of
equivalence points. Let‘s systematize it.
- 11 -

12. Equivalence &
Semi-Equivalence Points of H3A
Part 1a
Triprotic Acid

13. Triprotic Acid (H3A)
The 3-protic acid dissolves into 3+1 species:
H3A0 H2A-1 HA-2 A-3
There are several ways/equations
to define equivalence points
(including semi-equivalence points).
at least there are 23+1 EPs:
EPn with n = 0, ½, 1, ... 3
Note: We abbreviate the dissolved, neutral acid-species H3A0 also by H3A.

14. Triprotic Acid (H3A)
EP0 [H+] = [H2A-]
EP1/2 [H3A] = [H2A-]
EP1 [H3A] = [HA-2]
EP3/2 [H2A-] = [HA-2]
EP2 [H2A-] = [A-3]
EP5/2 [HA-2] = [A-3]
EP3 [HA-2] = [OH-]
H+ H3A H2A- HA-2 A-3 OH-
EP0 EP2
EP1 EP3
Equivalence Points
H3A H2A- HA-2 A-3
EP1/2 EP5/2
EP3/2
Semi-EPs

15. Triprotic Acid
1st diss. step: H3A = H+ + H2A- K1 = [H+][H2A-]/[H3A]
2nd diss. step: H2A- = H+ + HA-2 K2 = [H+][HA-2]/[H2A-]
3rd diss. step: HA-2 = H+ + A-3 K3 = [H+][HA-3]/[HA-2]
stepwise equilibrium constants
K1 = K1 = [H+]  pH = pK1
[H2A-] = [H3A]
(semi-EP)
[H+][H2A-]
[H3A]
K1K2 = K1K2 = [H+]2  pH = ½(pK1+pK2)
[HA-2] = [H3A]
(EP)
[H+]2[HA-2]
[H3A]
Each EP (or semi-EP) is characterized by one specific pH value
that relies directly on the acidity constants K: EP  pH  pK
pH = lg [H+]
pK = lg K

16. EP0 [H+] = [H2A-]
EP1/2 [H3A] = [H2A-]  pH1/2 = pK1
EP1 [H3A] = [HA-2]  pH1 = ½(pK1+pK2)
EP3/2 [H2A-] = [HA-2]  pH3/2 = pK2
EP2 [H2A-] = [A-3]  pH2 = ½(pK2+pK3)
EP5/2 [HA-2] = [A-3]  pH5/2 = pK3
EP3 [HA-2] = [OH-]
Each EP (or semi-EP) is characterized by one pH value
that relies directly on the acidity constants K: EP  pH  pK
The two “external EPs” EP0 and EP3 are non-trivial;
they depend, in addition, on the total amount of acid, CT.
- 16 -

17. EP1/2 EP1 EP3/2 EP2 EP5/2
pH1/2 pH1 pH3/2 pH2 pH5/2
phosphoric acid 2.15 4.68 7.21 9.78 12.35
citric acid 3.13 3.94 4.76 5.58 6.4
pK1 pK2 pK3
phosphoric acid 2.15 7.21 12.35
citric acid 3.13 4.76 6.4
pK1 pK2
EP1/2 EP1
pK3
pH
EP5/2EP2EP3/2
(midpoint) (midpoint)
pH1 pH2
EP0 EP3
Examples
- 17 -

18. Equivalence &
Semi-Equivalence Points of HNA
Part 1b
N-protic Acid
(N = 1, 2, 3, ...)

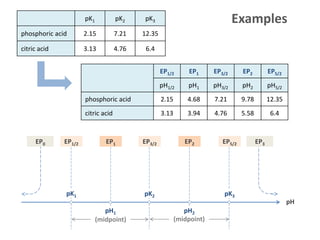
19. EP0 [H+] = [1]
EP1/2 [0] = [1]  pH1/2 = pK1
EP1 [0] = [2]  pH1 = ½(pK1+pK2)
EP3/2 [1] = [2]  pH3/2 = pK2
EP2 [1] = [3]  pH2 = ½(pK2+pK3)
⁞
EPN-½ [N-1] = [N]  pHN-½ = pKN
EPN [N-1] = [OH-]
An N-protic acid HNA has
internalEPs
two external EPs
and 2N+1 EPs:
N+1 acid-species: [j]  [HN-jA-j] with j = 0,1, ... N

20. N Acid HNA
EP1/2 EP1 EP3/2 EP2 EP5/2
pH1/2 pH1 pH3/2 pH2 pH5/2
1 acetic acid 4.76
2 (composite) carbonic acid 6.35 8.34 10.33
3 phosphoric acid 2.15 4.68 7.21 9.78 12.35
3 citric acid 3.13 3.94 4.76 5.58 6.4
Acid Type pK1 pK2 pK3
acetic acid HA 4.76
(composite) carbonic acid H2A 6.35 10.33
phosphoric acid H3A 2.15 7.21 12.35
citric acid H3A 3.13 4.76 6.4
Examples for Internal EPs

21. Unified Notation
for Internal EPs
EPn 
 pHn = ½ (pKn +pKn+1)
 pHn = pKn+1/2
[n-1] = [n+1]
[n-½] = [n+½]
integer n = j
(n = 1,2, ... N-1)
half-integer n = j-½
(n = ½, ³/₂, ... N-½)
semi-EPs:
Note: j is integer and indicates the acid-species [j] and acidity constants Kj;
n is integer and half-integer and labels the EPs and semi-EPs.
the true, chemical meaning of n
becomes clear in Part 2

22. External EPs
EPN [N-1] = [OH-]  pHN  14
EP0 [H+] = [1]  pH0  0
There is no simple relationship between EP  pH.
pH of EP0 and EPN depend on K1 to KN and on CT (= total
amount of acid).
However,
for CT   the following asymptotic behavior exists:
- 22 -

23. pH
CT[M]CT[M]
n=0 n=0.5 n=1.5n=1
n=2
n=0
n=0.5
n=1.5n=1 n=2
n=2.5
n=3
H3A (phosphoric acid)
H2A (carbonic acid)
Examples
Internal EPs:
red lines
(independent of CT)
External EPs:
blue & green lines
(CT-dependent)
Curves as dashed (and not solid) lines remind us that the simplified approach is an approximation.

24. Caution:
The simplified approach fails
for highly diluted acids
This restriction is
removed in the General Approach Part 2
(because self-ionization of H2O is ignored)

25. General Approach
based on Equivalent Fraction n
Part 2
n = CB/CT

26. (B+ = Na+, K+, NH4
+, ...)
n = =
CB amount of base
CT amount of acid
HNA BOH+ n
Titration of
weak acid HNA with strong base BOH
Equivalent Fraction n
- 26 -

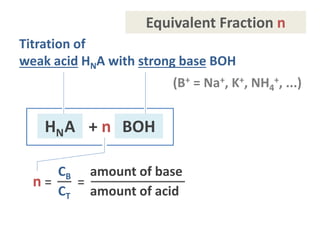
27. EP1  1 = CB /CT
EP½  ½ = CB /CT
EP1: [acid]T = [base]T
Generalization to other EPs:
EPn  n = CB /CT
⁞
CT CB T = total amount
- 27 -

28. equivalent fraction n =
CB
CT
Equivalent Points are special states
where the
n = 0, 1, ... N  EPn
n = ½, 3/2, ... N-½  semi-EPn
Definition
becomes an integer or half-integer
value:
- 28 -

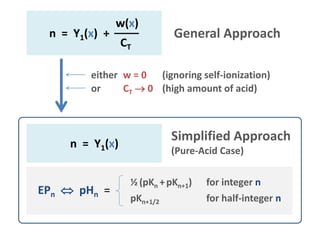
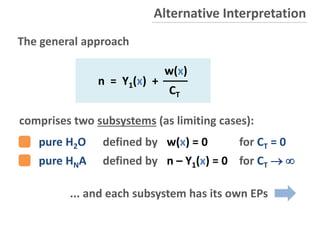
29. Basic Equation for HNA
n = Y1(x) +
w(x)
CT
self-ionization H2O
x
x
K
w w

N211 Naa2aY  
0j
j
j a
x
k
a 






1
N
N
2
21
0
x
k
...
x
k
x
k
1a








ionization fractions (j = 0, 1, ... N)
with
cumulative equilibrium constants: k1 = K1, k2 = K1K2, ...
total amount of acid
x  [H+] = 10-pH
Ref: www.aqion.de/file/acid-base-systems.pdf

30. Plots of EPn in pH-CT Diagrams
for an integer or half-integer n
you get from
one curve CT = CT(n,x) with x = 10-pH
)x(Yn
)x(w
C
1
T


n
Given: N-protic acid HNA  2N+1 curves
Note: You can perform the calculations by Excel, for example.
- 30 -

31. General Relationship
EPn  pHn
pH
n (Equivalent Fraction)
pH1/2 pH3/2pH0 pH1 pH2
EP1/2
EP3/2
EP0
EP1
EP2
Titration Curve of Diprotic Acid (Example: 100 mM H2CO3)
n = Y1(pH) +
w(pH)
CT

32. n=0 n=0.5 n=1
n=0 n=0.5 n=1 n=1.5
n=2
HA (acetic acid)
H2A (carbonic acid)
CT[M]
n=0
0.5 1.51 2 2.5
n=3
H3A (phosphoric acid)
n=0 0.5 1.51 2 2.5
n=3
H3A (citric acid)
pH
CT[M]
pH
EP & semi-EP
internal EP
external EP0
external EPN
dashed lines refer to the
“pure-acid case” in Part 1

33. n = Y1(x) +
w(x)
CT
General Approach
n = Y1(x)
Simplified Approach
(Pure-Acid Case)
either w = 0 (ignoring self-ionization)
or CT  0 (high amount of acid)
EPn  pHn =
½ (pKn +pKn+1) for integer n
pKn+1/2 for half-integer n

34. comprises two subsystems (as limiting cases):
pure H2O defined by w(x) = 0 for CT = 0
pure HNA defined by n – Y1(x) = 0 for CT  
n = Y1(x) +
w(x)
CT
The general approach
Alternative Interpretation
... and each subsystem has its own EPs
- 34 -

35. The general approach
decouples into two subsystems:
CT = 0 CT  
pure H2O pure HNA
with one single EP at pH 7 with EPn at pHn = ½(pKn +pKn+1)
and semi-EPn at pHn = pKn+1/2
w = 0 n – Y1 = 0 (poles of CT)
)x(Yn
)x(w
C
1
T

EPn 
- 35 -

36. The diagrams on the next two slides illustrate the situation
before and after both subsystems are joined together:
1st Diagram
The two uncoupled subsystems are located at both ends of the
CT scale:
• pure H2O at CT = 0 with one EP at pH 7
• pure acid at CT   with EPs at pHn
2nd Diagram
Starting at pH 7 the curves fan out when CT increases until they
fit the ‘pure acid’ values at the top of the chart.
- 36 -

37. Example H3PO4
CT[M]
pure acid (H3A)
pure H2O
two uncoupled subsystems
pH
pH=7
EP1/2 EP3/2EP1 EP2 EP5/2EP0 EP3
- 37 -

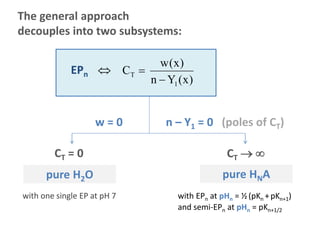
38. Example H3PO4
CT[M]
acid + H2O
pH
EP1/2 EP3/2EP1 EP2 EP5/2EP0 EP3
)x(Yn
)x(w
C
1
T


Coupling of two Subsystems
- 38 -

39. Summary

40. An N-protic acid has 2N+1 equivalence points:
EPn  n = CB /CT for n = 0, ½, 1, ... N
Equivalence points are special equilibrium states where
the equivalent fraction n = CB/CT becomes an integer or
half-integer value.
The relationship EPn  pHn is given by
where Y1 describes the acid and w the water.
n = Y1(pH) + w(pH)/CT
For high-concentrated acids (CT  ) the relationship
simplifies to: n = Y1(pH)
which yields the direct
link to acidity constants:
½ (pKn +pKn+1)  EP
pKn+1/2  semi-EP
pHn =

41. For high-concentrated acids (CT  ) there is
an alternative definition of EPs
based on equal species concentrations:
EPn: [n-1] = [n+1]
semi-EPn: [n-½] = [n+½]
Example: In carbonate systems EP1 is often introduced
as state where [H2CO3] = [CO3
-2].
The equivalent fraction n = Y1+ w/CT (titration curve)
describes the buffer capacity. Its pH-derivative is the
buffer intensity β = dn/dpH. EPs are extrema of β:
EPn  minimum buffer intensity
semi-EPn  maximum buffer intensity

42. Titration & Buffer Intensity
EPn (integer n)  minimum buffer intensity
semi-EPn (half-integer n)  maximum buffer intensity
pH
titration curve n(pH)
(buffer capacity)
buffer intensity β
EP1/2
EP3/2
EP0
EP1
EP2
pH1/2 pH3/2pH0 pH1 pH2
Diprotic Acid (100 mM H2CO3)

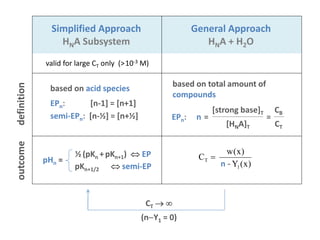
43. Simplified Approach
HNA Subsystem
General Approach
HNA + H2O
valid for large CT only (>10-3 M)
definition
based on acid species
EPn: [n-1] = [n+1]
semi-EPn: [n-½] = [n+½]
outcome
½ (pKn +pKn+1)  EP
pKn+1/2  semi-EP
pHn =
CT  
(nY1 = 0)
)x(Yn
)x(w
C
1
T


n
based on total amount of
compounds
EPn: n = =
[HNA]T
[strong base]T
CT
CB
- 43 -

44. Ref
www.aqion.de/file/acid-base-systems.pdf
www.aqion.de/site/68 (EN)
www.aqion.de/site/24 (DE)