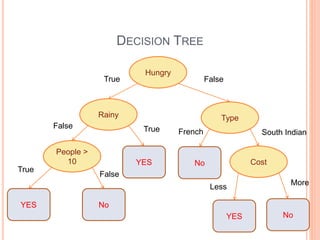
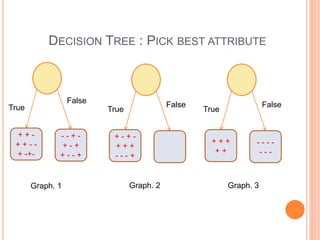
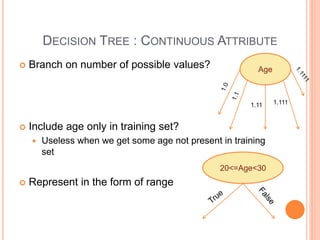
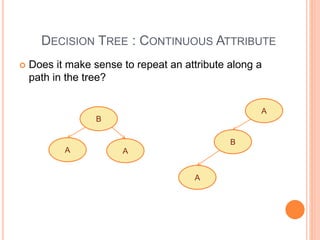
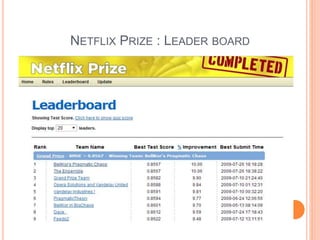
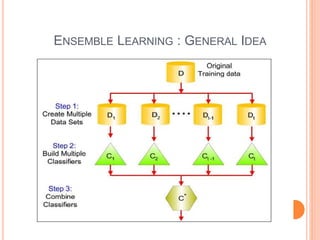
This document discusses decision trees, softmax regression, and ensemble methods in machine learning. It provides details on how decision trees use information gain to split nodes based on attributes. Softmax regression is described as a generalization of logistic regression for multi-class classification problems. Ensemble methods like bagging, random forests, and boosting are covered as techniques that improve performance by combining multiple models.

1. DECISION TREE, SOFTMAX
REGRESSION AND ENSEMBLE
METHODS IN MACHINE LEARNING
- Abhishek Vijayvargia

2. WHAT IS MACHINE LEARNING
 Formal Approach
 Filed of study that gives computers the ability to learn
without explicitly programmed.
 Informal Approach

3. MACHINE LEARNING
 Supervised Learning
 Supervised learning is the machine learning task of
inferring a function from labeled training data.
 Approximation
 Unsupervised Learning
 Trying to find hidden structure in unlabeled data.
 Examples given to the learner are unlabeled, there is no
error or reward signal to evaluate a potential solution.
 Shorter Description
 Reinforcement learning
 Learning by interacting with an environment

4. SUPERVISED LEARNING
 Classification
 Output variable takes class labels.
 Ex. Predicting a mail is spam/ham
 Regression
 Output variable is numeric or continuous.
 Ex. Measuring temperature

5. DECISION TREES
 Is this restaurant good?
 ( YES/ NO)

6. DECISION TREES
 What are the factors which decide that restaurant is
good for you or not?
 Type : Italian, South Indian, French
 Atmosphere: Casual, Fancy
 How many people inside it? (10< people > 30 )
 Cost
 Weather outside : Rainy, Sunny, Cloudy
 Hungry : Yes/No

7. DECISION TREE
Hungry
True False
Rainy
People >
10
YES No
YES
Type
Cost
YES No
No
True
False
True
False
French South Indian
More
Less

8. DECISION TREE LEARNING
 Pick best attribute
 Make a decision tree node containing that attribute
 For each value of decision node create a
descendent of node
 Sort training example to leaves
 Iterate on subsets using remaining attributes

9. DECISION TREE : PICK BEST ATTRIBUTE
True
+ + -
+ + - -
+ -+-
False
- - + -
+ - +
+ - - +
True
+ - + -
+ + +
- - - +
False
True
+ + +
+ +
False
- - - -
- - -
Graph. 1 Graph. 2 Graph. 3

10. DECISION TREE : PICK BEST ATTRIBUTE
 Select the attribute which gives MAXIMUM Information
Gain.
 Gain measures how well a given attribute separates
training examples into targeted classes.
 Entropy is a measure of the amount of uncertainty in the
(data) set.
H(S) = − 푥∈푋 푝(푥) log2 푝(푥)
S: Current data set for which entropy is calculated.
X: Set of classes in X.
p(x) : The proportion of the number of elements in class to
the number of elements in set.

11. DECISION TREE : INFORMATION GAIN
 Information gain IG(A) is the measure of the
difference in entropy from before to after the set S
is split on an attribute A.
 In other words, how much uncertainty in S was
reduced after splitting set S on attribute A.
IG(A,S) = H(S) - 푡∈푇 푝 푡 퐻(푡)
H(S) : Entropy of set S
T : The subsets created from splitting set S by
attribute A such that S = 푡∈푇 푡
p(t) : The proportion of the number of elements in t to
the number of elements in set S

12. DECISION TREE ALGORITHM : BIAS
 Restriction Bias : All type of possible decision tree.
 Preference Bias : Which decision tree algorithm
prefer?
 Good split at TOP
 Correct over Incorrect
 Shorter tree

13. DECISION TREE : CONTINUOUS ATTRIBUTE
 Branch on number of possible values?
 Include age only in training set?
 Useless when we get some age not present in training
set
 Represent in the form of range
Age
1.11 1.111
20<=Age<30

14. DECISION TREE : CONTINUOUS ATTRIBUTE
 Does it make sense to repeat an attribute along a
path in the tree?
B
A A
A
B
A

15. DECISION TREE : WHEN DO WE STOP?
 Everything classified correctly? (same example/
noisy two answer for same)
 No more attribute? ( not good for continuous
attribute/ infinite possibility)
 Pruning

16. SOFTMAX REGRESSION
 Softmax Regression ( or multinomial logistic
regression) is a classification method that
generalizes logistic regression to multiclass
problems. (i.e. with more than two possible discrete
outcomes.)
 Used to predict the probabilities of the different
possible outcomes of a categorically distributed
dependent variable, given a set of independent
variables (which may be real-valued, binary-valued,
categorical-valued, etc.).

17. LOGISTIC REGRESSION
 Logistic regression is used to refer specifically to
the problem in which the dependent variable is
binary ( only two categories).
 As output variable y ∈ 0,1 , it seems natural to
choose Bernoulli family of distribution to model
conditional distribution of y given x.
 Logistic function (which always takes on values
between zero and one)
퐹 푡 = 1
1+푒−푡 = 1
푒−휃푇푥

18. SOFTMAX REGRESSION
 Used in classification problem in which response
variable y can take on any one of k values.
 푦 ∈ 1,2, … , 푘 .
 Ex. Classify emails into three classes { Primary,
Social, Promotions }
 Response variable is still discrete but can take
more than two values.
 To derive General Linear Model for multinomial data
we begin by expressing the multinomial as an
exponential family distribution.

19. SOFTMAX REGRESSION
 To parameterize a multinomial over k-possible
outcomes, we could use k parameters ∅1, … , ∅푘
specifying probability of each outcomes.
푘 ∅푖 =
 These parameters are redundant because 푖=1
1. So ∅푖 = 푝 푦 = 푖; ∅
푘 ∅푖
 and 푝(푦 = 푘; ∅) = 1 − 푖=1
 Indicator Function 1{.} takes a value of 1 if it’s
argument is true, and 0 otherwise.
 1{True} = 1, 1{False} = 0.

20. SOFTMAX REGRESSION
 Multinomial is member of exponential family.
1{푦=1} ∅2
푝 푦; ∅ = ∅1
1{푦=2} … … . ∅푘
1{푦=푘}
1{푦=1} ∅2
= ∅1
1− 푖=1
1{푦=2} … … . ∅푘
푘−1{푦=푖}
=푏 푦 exp 휔푇 푇 푦 − a ω
Where 휔 =
log ∅ 1 ∅푘
log ∅ 2 ∅푘
⋮
log ∅ 푘 − 1 ∅푘
푎 휔 = − log ∅푘
푏 푦 = 1 푇 푦 ∈ 푅푘
_1

21. SOFTMAX REGRESSION
 The link function is given as
휔푖 = log
∅푖
∅푘
To invert the link function and derive the response
function
푒휔푖 =
∅푖
∅푘
∅푘푒휔푖 = ∅푖
∅푘
푘
푖=1
푒휔푖 =
푘
푖=1
∅푖 = 1

22. SOFTMAX REGRESSION
 So we get ∅푘= 1
푘 푒휔
푖=1
푖
we can substitute it back in
the equation to give response function
∅푖=
푒휔
푖
푘 푒휔
푖=1
푖
 Conditional distribution of y given x is given by
푝 푦 = 푖 푥; 휃 = 휔푖
=
푒휔
푖
푘 푒휔
푖=1
푖
=
푒−휃푖푇
푥
푖
푘 푒−휃푇
푖=1
푥
푖

23. SOFTMAX REGRESSION
 Softmax regression is a generalization of logistic
regression.
 Our Hypothesis will output
ℎ휃 푥 =
∅1
∅2
⋮
∅푘
 In other words, our hypothesis will output the
estimated probability 푝 푦 = 푖 푥; 휃 for every value of
i = 1, .. k.

24. ENSEMBLE LEARNING
 Ensemble learning use multiple learning algorithms
to obtain better predictive performance than could
be obtained from any of the constituent learning
algorithms.
 Ensemble learning is primarily used to improve the
prediction performance of a model, or reduce the
likelihood of an unfortunate selection of a poor one.

25. HOW GOOD ARE ENSEMBLES?
 Let’s look at NetFlix Prize Competition…

26. NETFLIX PRIZE : STARTED IN OCT 2006
 Supervised Learning Task
 Training Data is a set of users and rating (1,2,3,4,5
stars) those users have given to movies.
 Construct a classifier that given a user and an unrated
movie, correctly classified that movie as either 1,2,3,4 or
5 stars.
 $1 Million prize for a 10% improvement over Netflix
current movie recommender/Classifier.

27. NETFLIX PRIZE : LEADER BOARD

28. ENSEMBLE LEARNING : GENERAL IDEA

29. ENSEMBLE LEARNING : BAGGING
 Given :
 Training Set of N examples
 A class of learning models ( decision tree, NB, SVM,RF
etc. )
 Training :
 At each iteration I a training set Si of N tuples is
sampled with replacement from S.
 A classifier model Mi is learned for each training set Si.
 Classification : Classify an unknown sample x
 Each classifier Mi returns it’s class prediction.
 The bagged classifier M* count the votes and assign the
class with the most votes.

30. ENSEMBLE LEARNING : BAGGING
 Bagging reduces variance by voting/averaging.
 Can help a lot when data is noisy.
 If learning algorithm is unstable, then Bagging
almost always improves performance.

31. ENSEMBLE LEARNING : RANDOM FORESTS
 Random Forests grows many classification trees.
 To classify a new object from an input vector, put
the input vector down each of the trees in the
forest.
 Each tree gives a classification, and we say the tree
"votes" for that class.
 The forest chooses the classification having the
most votes (over all the trees in the forest).

32. ENSEMBLE LEARNING : RANDOM FORESTS
 Each tree is grown as follows:
 If the number of cases in the training set is N,
sample N cases at random - but with replacement,
from the original data. This sample will be the
training set for growing the tree.
 If there are M input variables, a number m<<M is
specified such that at each node, m variables are
selected at random out of the M and the best split
on these m is used to split the node. The value of m
is held constant during the forest growing.
 Each tree is grown to the largest extent possible.
There is no pruning.

33. FEATURES OF RANDOM FORESTS
 Better in accuracy among current algorithms.
 Runs efficiently on large data bases.
 It can handle thousands of input variables without
variable deletion.
 It gives estimates of what variables are important in
the classification.
 Effective method for estimating missing data and
maintains accuracy when a large proportion of the
data are missing.
 Generated forests can be saved for future use on
other data.

34. ENSEMBLE LEARNING : BOOSTING
 Create a sequence of classifiers, giving higher
influence to more accurate classifiers.
 At each iteration, make examples currently
misclassified more important( get larger weight in
the construction of the next classifier)
 Then combine classifier by weighted vote (weight
given by classifier accuracy)

35. ENSEMBLE LEARNING : BOOSTING
 Suppose there are just 7 training examples
{1,2,3,4,5,6,7}
 Initially each example has a 0.142 (1/7) probability of
being sampled.
 1st round of boosting samples ( with replacement) 7
examples { 3,5,5,4,6,7,3} and build a classifier from
them.
 Suppose examples {2,3,4,6,7} are correctly predicted by
this classifier and examples {1,5} are wrongly predicted:
 Weight of examples {1,5} are increased.
 Weight of examples {2,3,4,6,7} are decreased.
 2nd round of boosting again take 7 examples, but now
examples {1,5} are more likely to be sampled.
 And so on until some convergence is achieved.

36. ENSEMBLE LEARNING : BOOSTING
 Weights models according to performance.
 Encourage new model to become an “expert” for
instances misclassified by earlier model.
 Combines “Weak Learner” to generate “strong
learner”.

37. ENSEMBLE LEARNING
 Netflix 1st prize winner gradient boosted decision
tree.
 http://www.netflixprize.com/assets/GrandPrize2009
_BPC_BellKor.pdf

38. THANK YOU FOR YOUR ATTENTION

39.  Ask Question to narrow down possiblity
 Informatica building example
 Mango machine learning
 Cannot look all trees