1. 実践データ分析基礎
10 December 2014
Toshifumi Kuga CEO of TOSHI STATS SDN. BHD.
1

2. 目次
1. ワイン価格の予測式
2. データの扱い方（ベクトルと行列）
3. Rを使った線形回帰分析
2

3. 公開されているワイン価格の予測式
• オーリー・アッシェンフェルター教授
（Orley Ashenfelter アメリカ経済学会会長
2011）
• 1990年に公開
3
1. ワイン価格の予測式
http://www.liquidasset.com/winedata.html

4. ワイン価格＝-12.145+0.00117×冬の降雨+ 0.06163×育成期平
均気温- 0.00386×収穫期降雨+ 0.02385×1983年からの年数
• パラメータ：θ=[ -12.145, 0.00117, 0.06163, -0.00386, 0.02385 ]
• 説明変数：X=[1, 冬の降雨, 育成期平均気温, 収穫期降雨, 年数]
• ワイン価格：Y=θ0+θ1×X1＋θ2×X2+θ3×X3+θ4×X4
• ワイン価格は簡単に「Y=θX」と書けます！
4
1. ワイン価格の予測式
※「ワイン価格」は1961年の平均価格に対する当該年の平均価格の比を作りlogをとったもの、説明のため単純化してます

5. 価格予測のステップ
• ワイン価格：Y=θX
• Yは予測したい値（ここでは将来のワイン価格、まだわからない）
• Xは既知のデータ（過去の気温データ等は既にわかっている）
• パラメータθはまだわからない
→ θを求められれば、将来のワイン価格Yが求まります！
• 過去のYのデータも既知（過去のワイン価格も既にわかっている）
→ 過去のXとYのデータはセットで利用可能→これからθを求めます
5
1. ワイン価格の予測式

6. 分析に使われたデータ
6
1. ワイン価格の予測式
OBS VINT Y:LPRICE2 X1:WRAIN X2:DEGREES X3:HRAIN X4:TIME_SV
1 1952 -0.99868 600 17.1167 160 31
2 1953 -0.4544 690 16.7333 80 30
3 1954 430 15.3833 180 29
4 1955 -0.80796 502 17.15 130 28
5 1956 440 15.65 140 27
… … … … … … …
35 1986 563 16.2833 171 -3
36 1987 452 16.9833 115 -4
37 1988 808 17.1 59 -5
38 1989 443 82 -6
Y X

7. θの求め方：最小２乗法
• 観測された値（過去の価格）と予測値を比較してその差の
２乗和が最も小さくなるようにパラメータθを定めます
• コンピュータにより自動的に計算するプログラム（アルゴ
リズム）があります
• 実務上パラメータを手計算で求めることはまずありません
（ほとんどの場合手計算では解けない）
7
1. ワイン価格の予測式

8. コンピュータによるパラメータ計算
8
1. ワイン価格の予測式
過去の気温・価格等データ
Y パラメータを計算価格予測モデルが完成
θ
X
Y=θX

9. θとXは一つの数ではありません
• 数のあつまり、かたまり
• 数学で言えば、「ベクトル・行列」
• 大量の数をθ、Xとシンプルに表現できます！
• コンピュータではデータを「ベクトル・行列」で処理します
• R, MATLAB, pythonなど主なプログラム言語では「ベクト
ル・行列」を簡単に構成し、制御できます
9
1. ワイン価格の予測式

10. 「ベクトル・行列」に強くなりましょう！
• これがわかればデータの扱いが自由自在
• プログラムも自分で記述できます
• 実践データ分析の第一歩
10
1. ワイン価格の予測式

11. 2. データの扱い方（ベクトルと行列）
高校数学で学習した内容で充分です
• 演算を中心に説明します
• 四則演算以上のものではありません
• 初めは実際に手で計算して慣れる事をお勧め
します
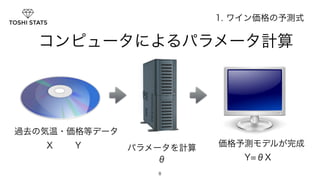
• 計算結果を確かめるためにRで検算しましょう
11

12. ベクトルは一行で表せます
12
• ベクトルの例
2. データの扱い方（ベクトルと行列）
［1 3 7］ ［5 13 ］
］
］5 1
b=c(5,13)
d=c(1,5)
a=c(1,3,7)
統計ツール「R」で確認しましょう

13. 2. データの扱い方（ベクトルと行列）
ベクトルの足し算
＋ ＝
6 7
2 7 ＋ ＝
13
［1 3 7］
］
］5 1
［２４ 1］
］
［3 7 8］
］
］
］
a=c(1,3,7)
b=c(2,4,1)
a+b
a=c(1,5)
b=c(6,2)
a+b

14. 2. データの扱い方（ベクトルと行列）
ベクトルの引き算
- ＝
6 -５
2 ３ - ＝
14
［1 ４ 7］
］
］5 1
［２３ 1］
］
［-１１ 6］
］
］
］
a=c(1,4,7)
b=c(2,3,1)
a-b
a=c(1,5)
b=c(6,2)
a-b

15. 2. データの扱い方（ベクトルと行列）
ベクトルの整数倍
3 ［２４ 1］
6 12
2 4 2 × ＝
15
］
［6 12 3］
］
× ＝
］
］
a=c(2,4,1)
3*a
b=c(6,2)
2*b

16. 2. データの扱い方（ベクトルと行列）
ベクトルのかけ算 (内積）
× ＝
16
［２４ 1］
］3
6 32
2
］
a=c(2,4,1)
b=c(3,6,2)
2×3+ 4×6+1×2 =32 a%*%b

17. 2. データの扱い方（ベクトルと行列）
行列の例
a=matrix(c(1,3,2,4),2,2) ２×２ ２×２ ３×２
• 次元：行の数×列の数 （m×nと表します）
17

18. 行列の要素
２行１列目の要素：３
18
• 行列の要素
2. データの扱い方（ベクトルと行列）
１行１列目の要素：１
１行２列目の要素：２
２行２列目の要素：４

19. 2. データの扱い方（ベクトルと行列）
行列の足し算
＋ =
19
＋
=

20. 2. データの扱い方（ベクトルと行列）
行列の引き算
ー=
20
ー
=

21. 2. データの扱い方（ベクトルと行列）
行列の整数倍・整数除
21
=
×
=
2 ×
/ 2 = 1/2

22. 2. データの扱い方（ベクトルと行列）
行列のかけ算
22
×
×
=
=
ちょっと
難しいかも？

23. 2. データの扱い方（ベクトルと行列）
かけ算を詳しくみてみましょう
［× 52 49］
［１ 2］ 3 4
［
a=matrix(c(1,3,2,4),2,2)
b=matrix(c(2,5,9,4),2,2)
1×9+ 2×4 =17
3×9+ 4×4 =43］＝
23
＝
a%*%b
［ 17］ 26 43
1×2+ 2×5 =12 12
3×2+ 4×5 =26

24. 2. データの扱い方（ベクトルと行列）
行列のかけ算は交換できません！
24
×
×
× = ×
=

25. 2. データの扱い方（ベクトルと行列）
ベクトルのかけ算 2
［２４］
25
］3
］6 × ＝ ［6 12］ 12 24
a=matrix(c(3,6),2,1)
b=c(2,4)
a%*%b

26. 2. データの扱い方（ベクトルと行列）
単位行列
• 対角が１で他の要素が0の行列
• 単位行列をかけても変わらない
× = × =
26
diag(2)

27. 2. データの扱い方（ベクトルと行列）
逆行列
• 行列が正方行列（行数＝列数）のとき、逆行列をかけ
ると単位行列になる
-１ -１
× = × =
a=matrix(c(1,3,2,4),2,2)
> a
[,1] [,2]
[1,] 1 2
[2,] 3 4
27
> inv=solve(a)
> inv
[,1] [,2]
[1,] -2.0 1.0
[2,] 1.5 -0.5
-１=

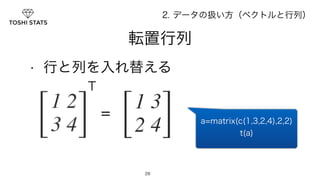
28. 転置行列
28
2. データの扱い方（ベクトルと行列）
• 行と列を入れ替える
a=matrix(c(1,3,2,4),2,2)
t(a)
=
T

29. 最小２乗法への応用
• ベクトルのかけ算を最小２乗法の計算に使ってみます
• J = 1/(2*m) * T(X*θ-Y)*(X*θ-Y) ： コスト関数と呼ばれます
• mはサンプル数
• XとYは既知のデータ、θはパラメータ
• T（ ）は転置行列を表します
• Jが最小になる(実際の値と予測値が近い）θをみつける
29
→最小２乗法
2. データの扱い方（ベクトルと行列）

30. 線形回帰関数『lm』で分析
> wineprice=lm(LPRICE2~WRAIN+DEGREES+HRAIN+TIME_SV, data=wine)
> wineprice
30
3. Rでの線形回帰分析
lmのあとに予測したい変数、そのあとに”~”と説明変数、data=のあとに使うデータ名（このwineは行列です！）を入力
> ▼▼▼=lm(◯◯◯~△△△+■■■, data=◎◎◎)
> ▼▼▼
説明変数
予測したい変数
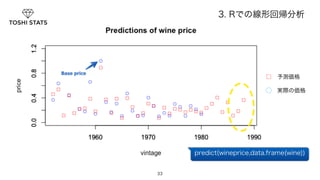
http://www.liquidasset.com/winedata.html データはこちら

31. 3. Rでの線形回帰分析
パラーメータが求まりました！
• Call:
• lm(formula = LPRICE2 ~ WRAIN + DEGREES + HRAIN + TIME_SV,
ワイン価格の予測式と比べてみましょう
31
data =wine)
• Coefficients:
• (Intercept) WRAIN DEGREES HRAIN TIME_SV
• -12.145007 0.001167 0.616365 -0.003861 0.023850

32. 32
3. Rでの線形回帰分析
RStudio
see p38

33. 33
3. Rでの線形回帰分析
□ 予測価格
◯ 実際の価格
predict(wineprice,data.frame(wine))

34. データ分析も関数で自動計算！
• 線形関数「lm」を使えば１行で分析を実行し、パラメータを求めることができます
• Rには様々な関数が用意されており、それらを利用すれば高度なデータ分析もすぐに
実行可能
• ただし、関数がどのような計算をしているのか概略の理解は必要。ブラックボック
ス化は危険
• 関数の理解が深まれば、どのようなケースにどの関数を使えば良いか判断できます
• まずは線形関数「lm」を使いこなしてみましょう。これがわかれば他の関数の理解
も容易になります
34
3. Rでの線形回帰分析

35. レコメンダーシステム
• amazon.comやNetflixのレコメンデー
ションが有名
• 様々なレコメンデーションが実用化
• 人気投票で第1位の商品を推奨
→だれにでも同じものを推奨
• 購買履歴から顧客毎に最適な商品を推奨
→効果的なパーソナライズ手法が必要
35

36. パーソナライゼイション
• パーソナライズされたレコメンデーションの求め方の一例
• θ：顧客の趣向（当該商品をクリックしたか？、当
該商品にレーティングを付与したか？）
• X：商品の属性（映画の場合：ホラー・ロマンス・
SF・監督・主役・年代・制作国など）
• ロジスティック回帰分析を用いθXから確率を求める
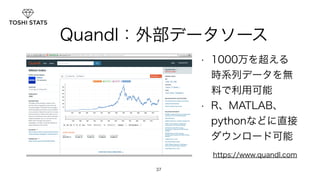
• 確率が高い場合、顧客にその商品を推奨する
36

37. Quandl：外部データソース
37
• 1000万を超える
時系列データを無
料で利用可能
• R、MATLAB、
pythonなどに直接
ダウンロード可能
https://www.quandl.com

38. Website of R and RStudio
• 弊社のwebでRの入門コースが閲覧できます. ダウンロードの方法も紹介していま
す。無料ですので覗いてみて下さい
http://www.toshistats.net/introduction-to-r-language/
• Rは以下のwebからダウンロードできます。R is a language and environment
for statistical computing. R Foundation for Statistical Computing, Vienna,
Austria. ISBN 3-90005107-0 URL http://www.R-project.org
• RStudio は Rの統合開発環境(IDE)で最も優れたものの一つです. 無料で利用可能
http://www.rstudio.com/products/rstudio/download/
38

39. Thanks for your attentions
• TOSHI STATS SDN. BHD. Digital-learning center for statistical computing in
Asia
• CEO : Toshifumi Kuga, Certified financial services auditor
• Company web site : www.toshistats.tokyo (日本語のサイトです）
• Company blog : http://toshistats.wordpress.com/aboutme/
• Company FB page : www.facebook.com/toshistatsco
• ブログはデータ分析の最新情報を御伝えするため毎週木曜日の10:00に更新してます !
39

40. Disclaimer
• TOSHI STATS SDN. BHD. and I do not accept any responsibility or
liability for loss or damage occasioned to any person or property
through using materials, instructions, methods, algorithm or ideas
contained herein, or acting or refraining from acting as a result of
such use. TOSHI STATS SDN. BHD. and I expressly disclaim all
implied warranties, including merchantability or fitness for any
particular purpose. There will be no duty on TOSHI STATS SDN.
BHD. and me to correct any errors or defects in the codes and the
software
© 2014 TOSHI STATS SDN. BHD. All rights reserved
40