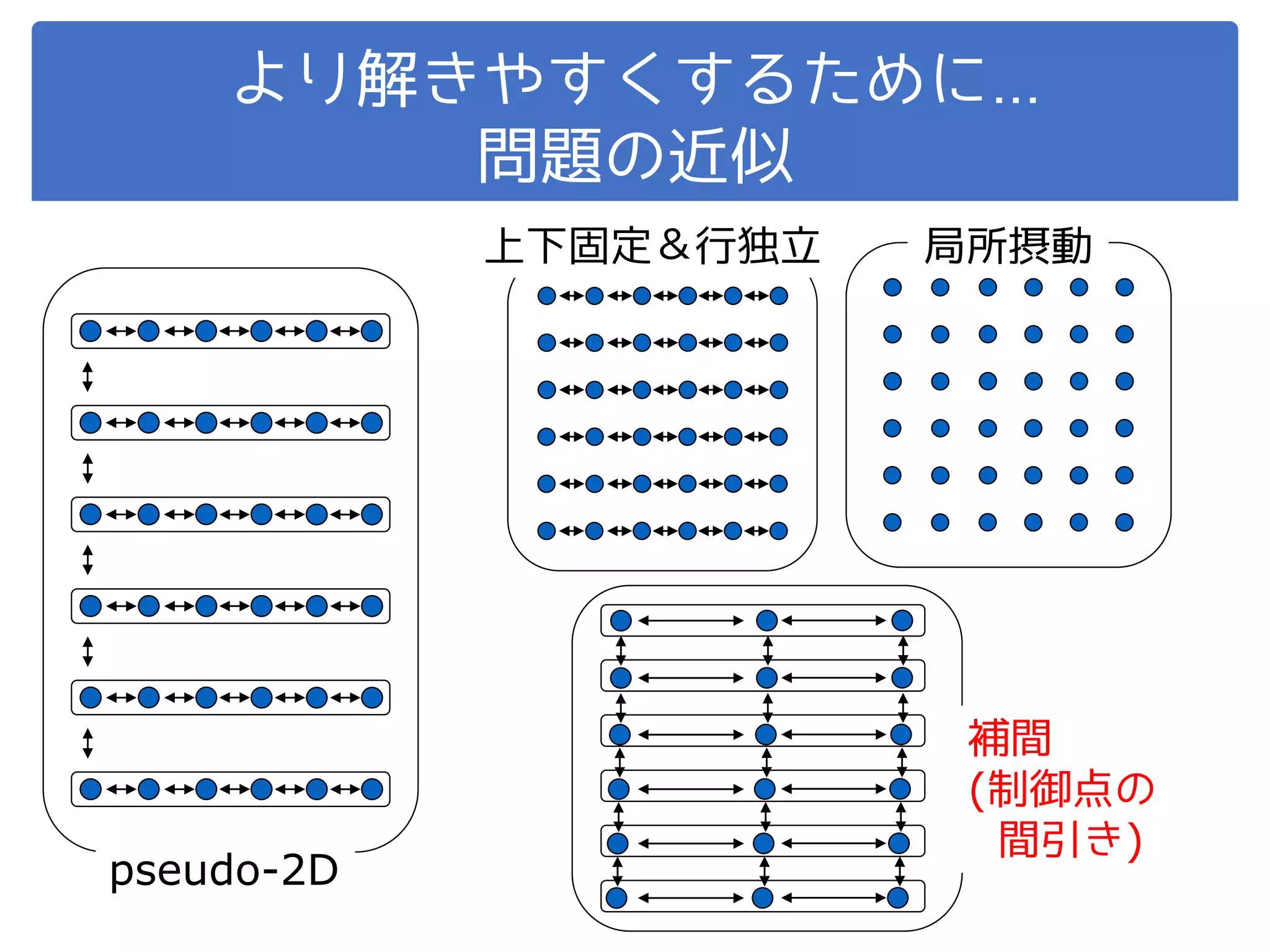
動的計画法(DP)は,バイオインフォマティクスのペアワイズアライメントの基本技術として,生物学においても広く知られていることと思います.古典的ながら,大局的最適解が保証される点をはじめ,実装が簡単、数値的に安定、学習も不要、多様な応用・拡張が可能といった利点を持っています.この性質から,画像情報学分野においても,アライメント(マッチング)だけでなく,トラッキングやセグメンテーションなど様々に利用されています.本講演ではDPの原理や用途,使いこなすためのノウハウ,そしていくつかの発展形についてご紹介いたします.