Shinichi Mogami, Norihiro Takamune, Daichi Kitamura, Hiroshi Saruwatari, Yu Takahashi, Kazunobu Kondo, Hiroaki Nakajima, and Nobutaka Ono,
in Proc. 2018 Autumn Meeting of Acoustical Society of Japan, 2018, pp. 215--218.
最上伸一, 高宗典玄, 北村大地, 猿渡洋, 高橋祐, 近藤多伸, 中嶋広明, 小野順貴,
「一般化反復射影法に基づく時変劣ガウス独立低ランク行列分析」,
日本音響学会2018年秋季研究発表会3-1-10,215--218ページ

![独立低ランク行列分析 (ILRMA) [Kitamura+, 2016]
⋄ ブラインド音源分離手法の一つ
Time
Frequency
Frequency
Time
STFT周波数毎の
分離行列
観測信号 分離信号 低ランク近似 (NMF)
(i:周波数インデックス,j:時間インデックス,n:音源インデックス)
⋄ 以下の条件を満たす分離行列 Wi と音源モデル Tn, Vn を求める
▶ 分離信号間が互いに独立である
▶ 個々の分離信号が低ランクな時間周波数構造を持つ
⋄ 分離行列 Wi の更新と音源モデル Tn, Vn の更新を交互に反復
1 / 18](https://image.slidesharecdn.com/all-180918053718/75/slide-2-2048.jpg)
![GGD-ILRMA [Kitamura+, 2018], [Ikeshita+, 2018]
⋄ 複素一般化 Gauss 分布 (GGD) に基づく ILRMA
▶ 音源の生成モデルに原点対称な時変複素 GGD を用いる
▶ 形状⺟数 β を変えると分布形状(尖度)が変わる
▶ 音源の特性に合致した β を選べば性能向上が期待できる
▶ β > 2 における効率的かつ収束性の保証された更新則は未提案
0 < β ≤ 2 β = 2 β > 2
優ガウス分布 ガウス分布 劣ガウス分布
(尖度大) (尖度小)
(β = 1) (β = 4)
2 / 18](https://image.slidesharecdn.com/all-180918053718/75/slide-3-2048.jpg)


![GGD-ILRMA の更新式:分離行列 Wi
⋄ 最小化したいコスト関数(Wi にのみ注目):
LGGD = −2J
∑
i
log |det Wi| +
∑
i,j,n
wH
inxij
β
rijn
β
+ const.
⋄ 従来法:MM 法 + 反復射影法 (IP) [Ono, 2011]
1. |wHx|β を w の二次形式で上からおさえる補助関数を設計
LGGD ≤ −2J
∑
i
log |det Wi| + J
∑
i,n
wH
inFinwin + const.
2. 補助関数に IP を適用
⋄ 問題点:従来法は劣ガウス GGD-ILRMA には適用できない!
▶ IP は− log det 項と二次形式の和の形にのみ適用可能
▶ しかし,β > 2 のときは |z|β
を |z|2
で上から評価できない
Ex. |z|
4
を上からおさえられる 2 次関数は存在しない
5 / 18](https://image.slidesharecdn.com/all-180918053718/75/slide-6-2048.jpg)

![一般化 IP:分離行列最適化における変数分離
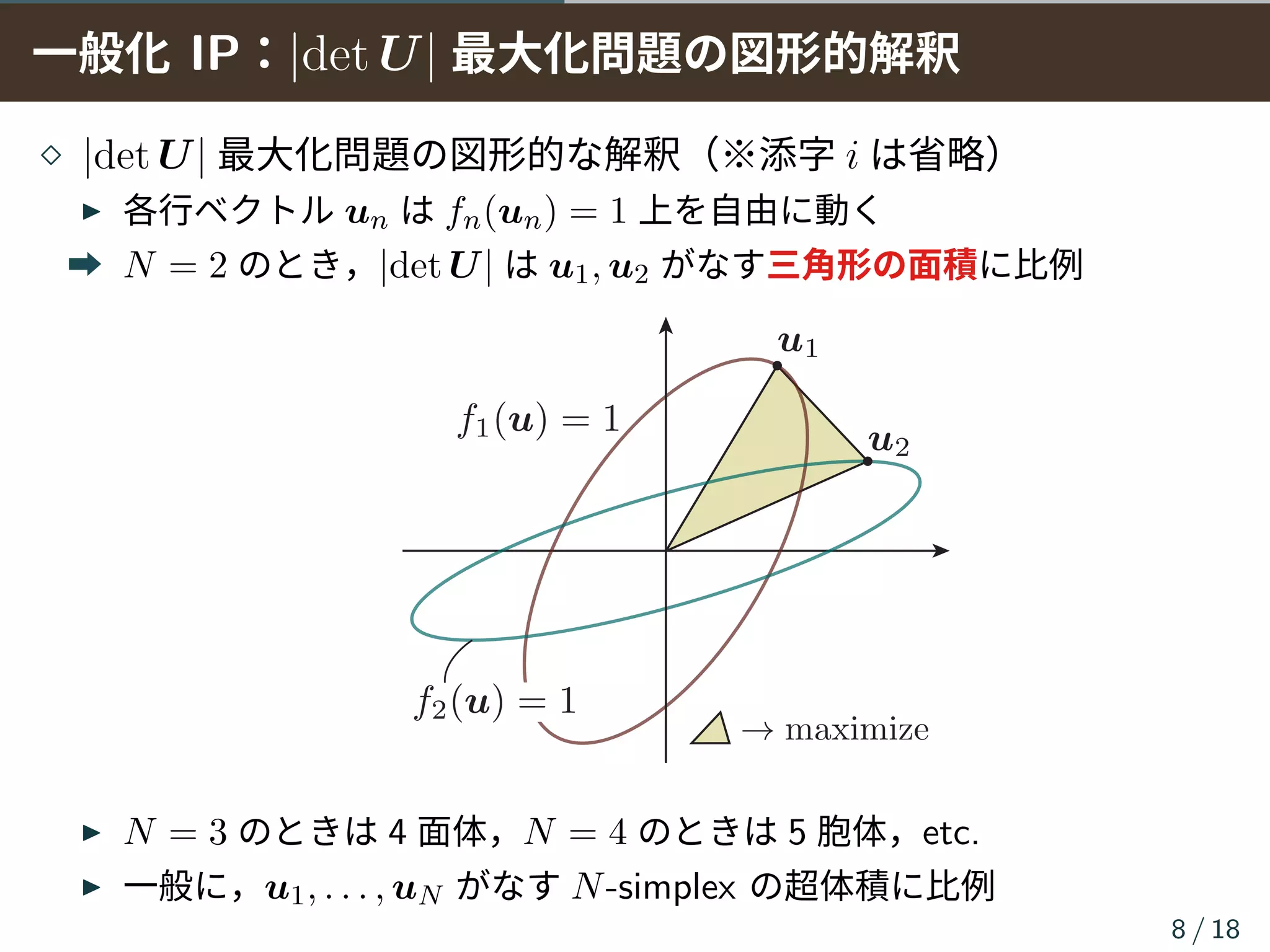
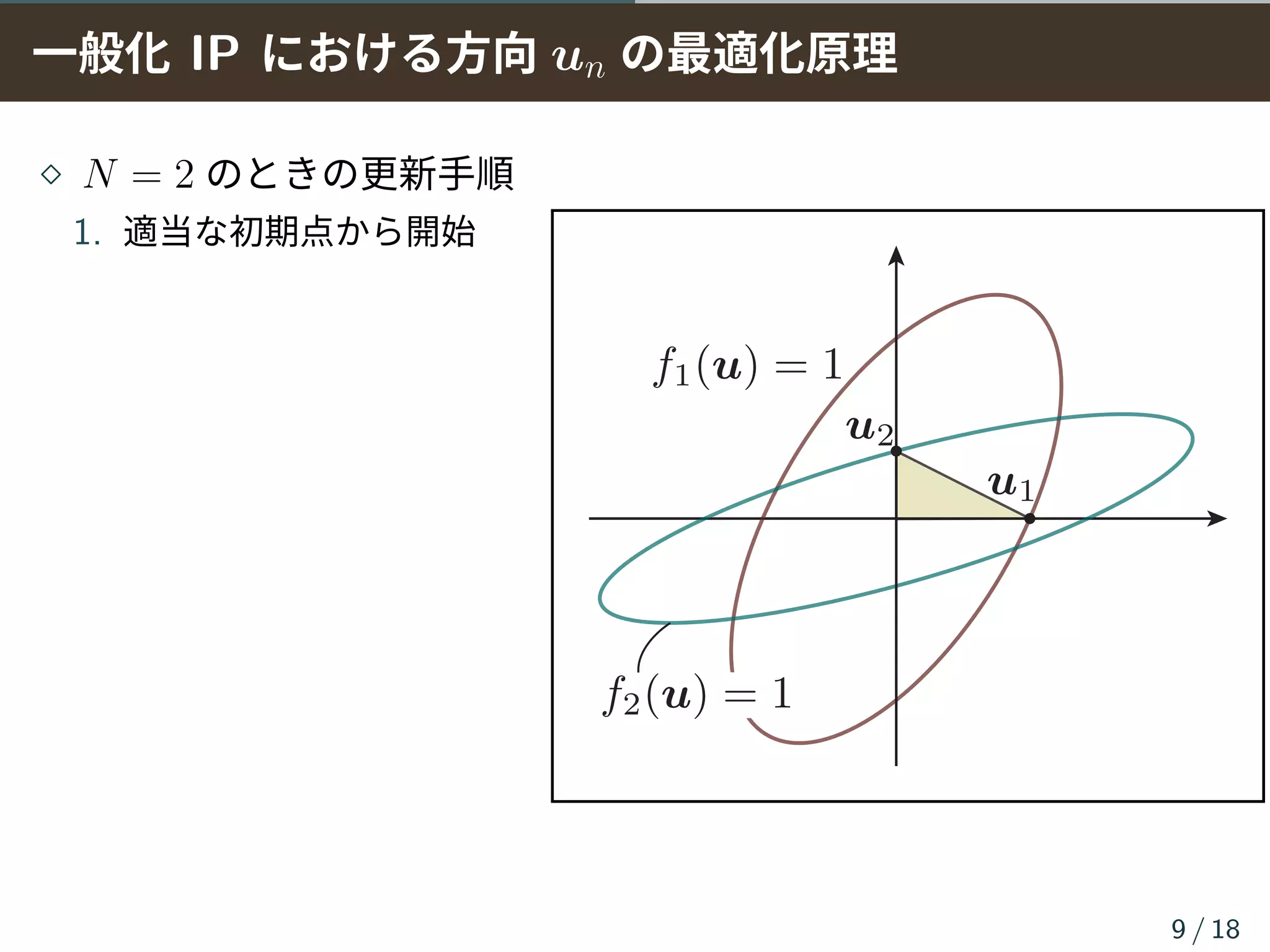
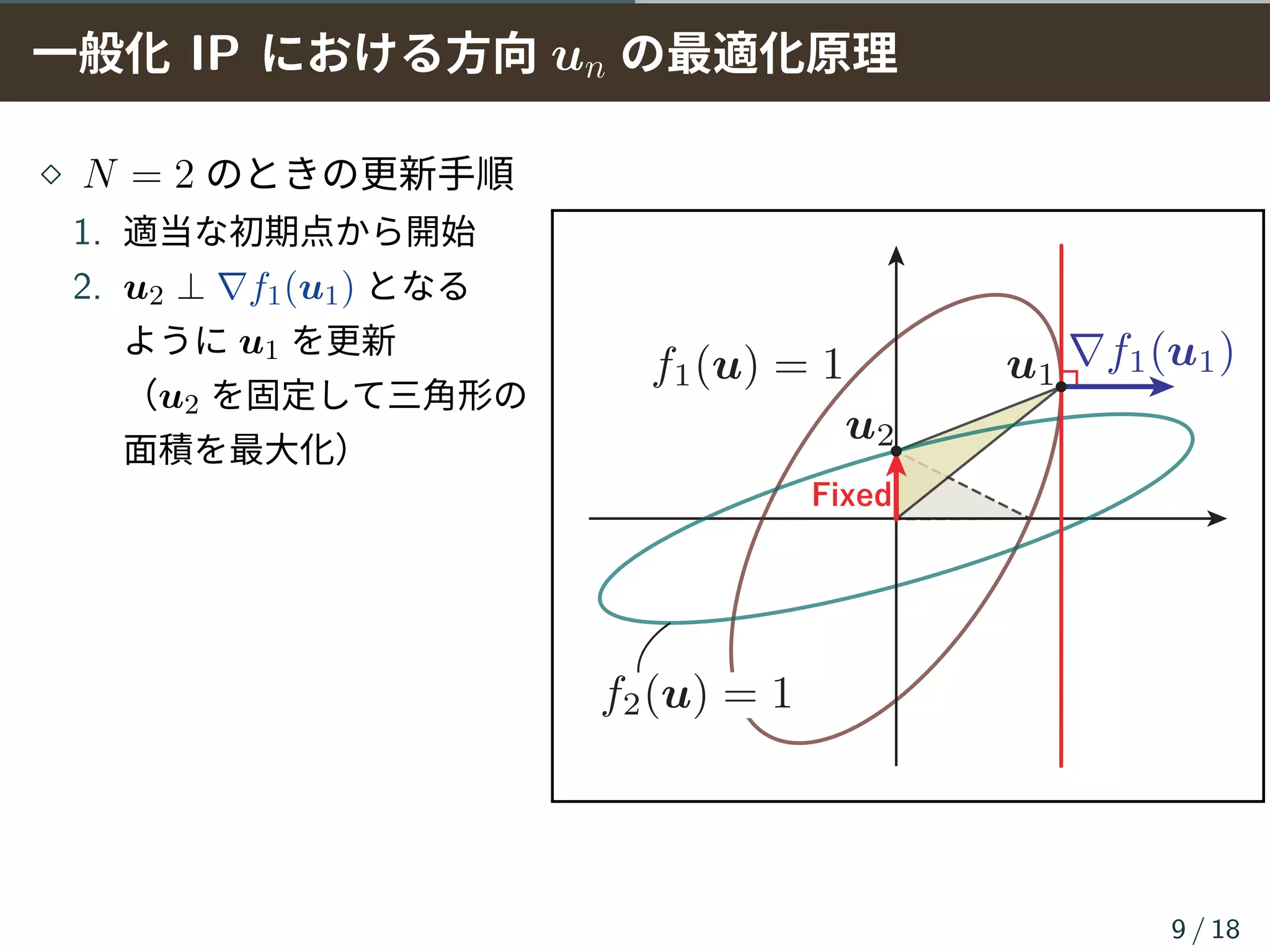
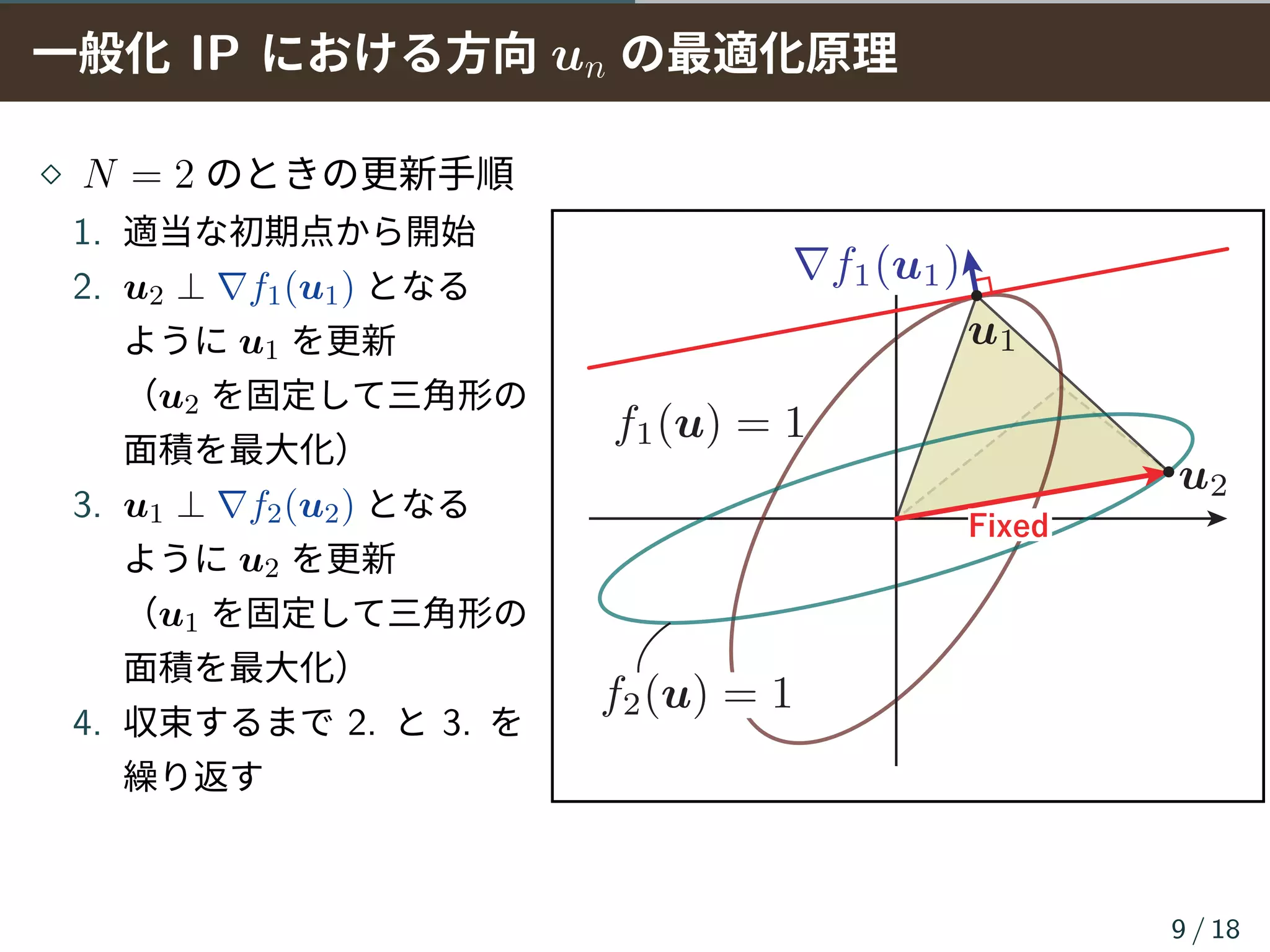
⋄ 分離行列の各行ベクトルを win = ηinuin と分けてコストを記述
▶ uin は fin(uin) = 1 を満たすベクトル(win の方向を表す)
▶ ηin は正の実数(win のスケールを表す)
L = −2 log |det Wi| +
N∑
n=1
fin(win)
= −2 log det
[
ηi1ui1 · · · ηiN uiN
]H
+
N∑
n=1
fin(ηinuin)
= −2 log
(
∏
n
ηin · |det Ui|
)
+
N∑
n=1
ηin
d
fin(uin)
= −2 log |det Ui| +
N∑
n=1
[
−2 log ηin + ηin
d
]
➡ Ui = [ui1, · · · , uiN ]H
の行列式の絶対値を最大化する問題に帰着
7 / 18
容易に最小化可能
ηin = (2/d)1/d](https://image.slidesharecdn.com/all-180918053718/75/slide-8-2048.jpg)




![β = 4 における GGD-ILRMA の補助関数
定理 1 ※詳細は予稿参照
任意の ˜w ∈ CN をとり
H =
[
1
r1
x1 · · · 1
rJ
xJ
]
,
˜q =
[
˜q1 · · · ˜qJ
]
= HH
˜w,
G = H ·
1
√
J
∑
j |˜qj|
4
∥˜q∥
2
−˜q1 ˜q∗
2 · · · −˜q1 ˜q∗
J
−˜q2 ˜q∗
1 ∥˜q∥
2
· · · −˜q2 ˜q∗
J
...
...
...
...
−˜qJ ˜q∗
1 −˜qJ ˜q∗
2 · · · ∥˜q∥
2
· HH
とすると,任意の w に対して
1
J
J∑
j=1
|wH
xj|4
rj
4
≤ (wH
Gw)2
となり,w = ˜w のとき等号が成立する.
※ 一般化 IP の式は ∇(w′H
Gu)2 = (w′H
Gw′)Gw′ ∥ W −1
i en となり,
解きやすい線形方程式に帰着 (w′ ∥ G−1W −1
i en)
12 / 18
特殊な係数行列
G を持つ
二次形式の二乗](https://image.slidesharecdn.com/all-180918053718/75/slide-17-2048.jpg)
![β = 4 における GGD-ILRMA の更新式
以下の更新を周波数及び n = 1, . . . , N について繰り返す.
1. 方向の最適化
Hin =
[
1
ri1n
xi1 · · · 1
riJn
xiJ
]
,
qin =
[
qi1n · · · qiJn
]⊤
= HH
inwin,
Gin = Hin ·
1
√
J
∑
j |qijn|
4
∥qin∥
2
−qi1nq∗
i2n · · · −qi1nq∗
iJn
−qi2nq∗
i1n ∥qin∥
2
· · · −qi2nq∗
iJn
...
...
...
...
−qiJnq∗
i1n −qiJnq∗
i2n · · · ∥qin∥
2
· HH
in,
win ← G−1
in W −1
i en
2. スケールの最適化
win ← w′
in
4
√
J
2
∑
j(|w′
in
H
xin|4
/rijn
4
)
13 / 18](https://image.slidesharecdn.com/all-180918053718/75/slide-18-2048.jpg)
![評価実験:概要
⋄ ILRMA による音楽信号の分離
▶ 2 音源の音楽信号の混合音を 6 種類用意
▶ 音楽信号の生成には Microsoft GS Wavetable Synth を使用
▶ 音楽信号は劣ガウス信号になりやすい [Naik+, 2012]
➡ 時変劣ガウス分布に基づく提案手法が高い性能を示すと考えられる
⋄ ILRMA による音声信号の分離
▶ 2 音源の音声信号の混合音を 4 種類用意
▶ 音声信号は MIDI 音源に比べて劣ガウス性が弱いと考えられる
➡ 時変劣ガウス分布は優ガウス分布も表せるから,提案手法も従来法と
同程度には分離できると期待できる
14 / 18](https://image.slidesharecdn.com/all-180918053718/75/slide-19-2048.jpg)



