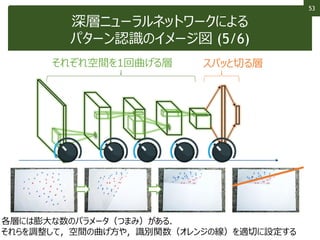
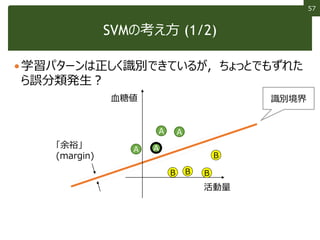
The document discusses pattern recognition and classification. It begins by defining pattern recognition as a method for determining what something is based on data like images, audio, or text. It then provides examples of common types of pattern recognition like image recognition and speech recognition. It notes that while pattern recognition comes easily to humans, it can be difficult for computers which lack abilities like unconscious, high-speed, high-accuracy recognition. The document then discusses the basic principle of computer-based pattern recognition as classifying inputs into predefined classes based on their similarity to training examples.






![7
それでも身近になりつつあるパターン認識:
画像認識の例
顔認識
物体認識
食事認識(さらにカロリー推定)
医用画像認識
電気通信大学 柳井研究室
https://mm.cs.uec.ac.jp/research/?res=naritomi-s&utf8=1
[Natarajan+, JAMA Ophthalmol., 2019]
Mtheiler@Wikipedia 物体検出](https://image.slidesharecdn.com/13-210821073957/85/13-7-320.jpg)