Download to read offline
![[DL輪読会]Scalable Training of Inference Networks for Gaussian-Process Models](https://cdn.slidesharecdn.com/ss_thumbnails/mainslideshare1-190927025239-thumbnail.jpg?width=640&height=640&fit=bounds)
![[PRML] パターン認識と機械学習（第1章：序論）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter1-170903070406-thumbnail.jpg?width=640&height=640&fit=bounds)
一般化線形モデル
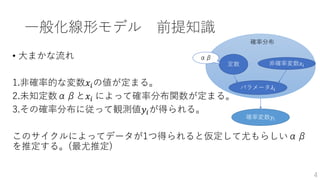
- 1.
- 2.
- 3.
- 4. 一般化線形モデル 前提知識 • 大まかな流れ 1.非確率的な変数𝑥𝑖の値が定まる。 2.未知定数αβと𝑥𝑖によって確率分布関数が定まる。 3.その確率分布に従って観測値𝑦𝑖が得られる。 このサイクルによってデータが1つ得られると仮定して尤もらしいαβ を推定する。(最尤推定) 定数 パラメータ𝜆𝑖 確率変数𝑦𝑖 確率分布 αβ 非確率変数𝑥𝑖 4
- 5.
- 6.
- 7.
- 8. GLMM 最尤推定 場所差・個体差を表すランダム効果の導入 𝑔(𝜆𝑖) =𝛼 + 𝛽𝑥𝑖 + 𝑟𝑖 ランダム効果の項＝個体差パラメーターはすべての個体で独立 に同じ正規分布に従うと仮定する。(平均０) ∀𝑖 , 𝑟𝑖~𝑁(0, 𝑠2 ) 固定効果 ランダム効果ある確率分布のパラ メータとリンク関数 個体差によって GLMの予測から多 少はずれてしまう ことを表す 8
- 9. GLMM 最尤推定 𝑟1 𝑟2 𝑟𝑛 従来通り最尤推定すると推 定すべきパラメータが (観測回数＋変数の数+2)個 rの数βの次元 𝛼, 𝑠2 ここだけを自分 で決定できる 定数 確率変数 パラメータ𝜆𝑖 確率変数𝑦𝑖 正規分布 ある確率分布 ここだけを観測 できる 𝑟𝑖αβ 𝑠2 非確率変数𝑥𝑖 反復 9
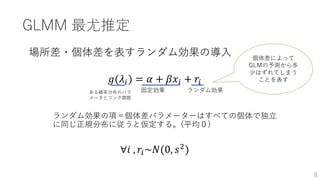
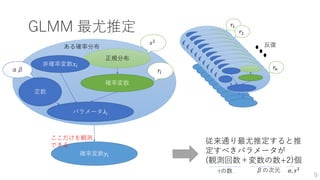
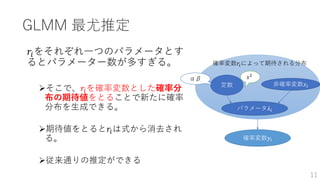
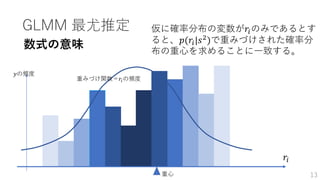
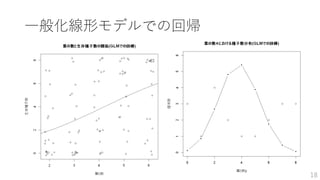
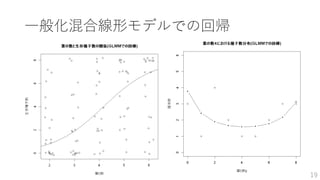
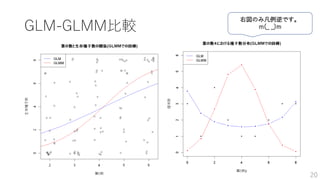
- 10. GLMM 最尤推定 式に表すと、 𝑔(𝜆𝑖) =𝛼 + 𝛽𝑥𝑖 + 𝑟𝑖 (𝑟𝑖~𝑁 0, 𝑠2 , 𝑔: リンク関数) 𝐿𝑖(𝑦𝑖) = 𝑓 𝑦𝑖 𝜆𝑖 = 𝑓 𝑦𝑖 𝛼, 𝛽, 𝑟𝑖, 𝑠2 (𝑓: 確率分布関数) 𝐿 = 𝑖 𝐿𝑖 = 𝑖 𝑝 𝑦𝑖 𝛼, 𝛽, 𝑟𝑖, 𝑠2 𝛼, 𝛽, 𝑠2 , 𝑟1, 𝑟2, , , , 𝑟𝑛 に依存する 10
- 11.
- 12. GLMM 最尤推定 つまり、新たな確率分布𝑓′を下のように定義する。 𝑓′ (𝑦𝑖|𝛼, 𝛽,𝑠2 ) = −∞ ∞ 𝑓(𝑦𝑖| 𝛼, 𝛽, 𝑟𝑖)𝑝 𝑟𝑖 𝑠2 𝑑𝑟𝑖 12
- 13.
- 14.
- 15. GLMM 最尤推定 新たにできた確率分布関数を使うと尤度は以下のように 計算できる。 𝐿𝑖 𝑦𝑖= 𝑓′ (𝑦𝑖|𝛼, 𝛽, 𝑠2 ) = −∞ ∞ 𝑓 𝑦𝑖 𝛼, 𝛽, 𝑟𝑖)𝑝 𝑟𝑖 𝑠2 𝑑𝑟𝑖 𝐿 = 𝑖 𝐿𝑖 = 𝑖 −∞ ∞ 𝑓 𝑦𝑖 𝛼, 𝛽, 𝑟𝑖)𝑝 𝑟𝑖 𝑠2 𝑑𝑟𝑖 15
- 16. 例題 問) 植物の葉の枚数と種子の生存比率の関係を回帰する。 • 植物の葉を枚数を観測し説明変数xとする。 •種子をランダムに8つ選び、その生存数を数える。 • データは次ページ ⇒二項分布とできる。(試行数：８) （一般化線形モデルの資料を参照） 16
- 17.
- 18.
- 19.
- 20.
- 21.
- 22. 参考文献 データ解析のための統計モデリング入門: 一般化線形モデル・階 層ベイズモデル・MCMC • 著者:久保拓弥 • 出版社: 岩波書店, シリーズ「確率と情報の科学」 • 編集: 甘利俊一，麻生英樹，伊庭幸人 22