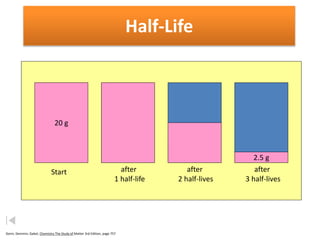
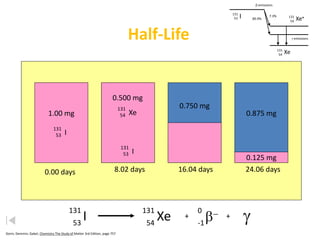
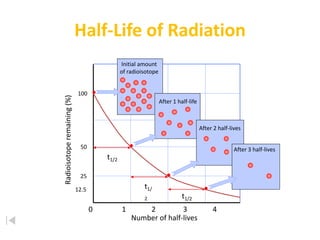
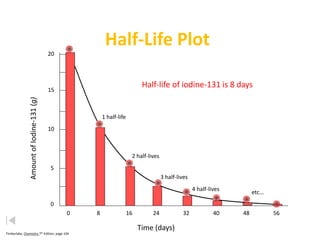
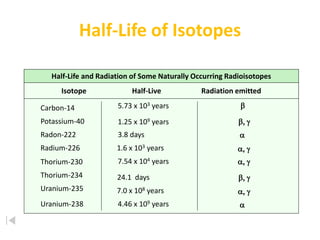
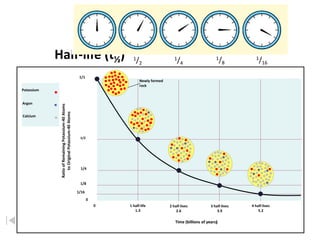
The document contains information about radioactive decay and half-lives. It includes tables and graphs showing how the amount of a radioactive substance decreases over time and after successive half-lives. Examples are provided for different radioactive isotopes, including carbon-14 and iodine-131. Calculations are presented for determining the age of samples and amount of material remaining after a given number of half-lives.

1. Half-Life

2. 20 g
10 g
5 g
2.5 g
after
1 half-life
Start after
2 half-lives
after
3 half-lives
Dorin, Demmin, Gabel, Chemistry The Study of Matter 3rd Edition, page 757
Half-Life

3. 1.00 mg 0.875 mg
0.500 mg
0.250 mg
0.125 mg
8.02 days0.00 days 16.04 days 24.06 days
Half-Life
Dorin, Demmin, Gabel, Chemistry The Study of Matter 3rd Edition, page 757
131
53 I
131
53 I
0.500 mg
0.750 mg
b emissions
g emissions
89.9%
7.3%
131
53 I
131
54 Xe
131
54 Xe*
131
54 Xe
I
131
53
Xe
131
54
b-0
-1
+ g+

4. 0 1 2 3 4
Number of half-lives
Radioisotoperemaining(%)
100
50
25
12.5
Half-Life of Radiation
Initial amount
of radioisotope
t1/2
t1/
2 t1/2
After 1 half-life
After 2 half-lives
After 3 half-lives

5. Half-Life Plot
Timberlake, Chemistry 7th Edition, page 104
AmountofIodine-131(g)
20
15
10
5
0
40 48 560 8
1 half-life
16
2 half-lives
24
3 half-lives
32
4 half-lives
etc…
Time (days)
Half-life of iodine-131 is 8 days

6. Half-Life of Isotopes
Isotope Half-Live Radiation emitted
Half-Life and Radiation of Some Naturally Occurring Radioisotopes
Carbon-14 5.73 x 103 years b
Potassium-40 1.25 x 109 years b, g
Thorium-234 24.1 days b, g
Radon-222 3.8 days a
Radium-226 1.6 x 103 years a, g
Thorium-230 7.54 x 104 years a, g
Uranium-235 7.0 x 108 years a, g
Uranium-238 4.46 x 109 years a

7. Half-life (t½)
– Time required for half the atoms of a
radioactive nuclide to decay.
– Shorter half-life = less stable.
1/2
1/4
1/8
1/16
1/1
1/2
1/4
1/8
1/16
0
RatioofRemainingPotassium-40Atoms
toOriginalPotassium-40Atoms
0 1 half-life
1.3
2 half-lives
2.6
3 half-lives
3.9
4 half-lives
5.2
Time (billions of years)
Newly formed
rock
Potassium
Argon
Calcium

8. How Much Remains?
After one half-life, of the original atoms remain.
After two half-lives, ½ x ½ = 1/(22) = of the original atoms remain.
After three half-life, ½ x ½ x ½ = 1/(23) = of the original atoms remain.
After four half-life, ½ x ½ x ½ x ½ = 1/(24) = of the original atoms remain.
After five half-life, ½ x ½ x ½ x ½ x ½ = 1/(25) = of the original atoms remain.
After six half-life, ½ x ½ x ½ x ½ x ½ x ½ = 1/(26) = of the original atoms remain.
1
4
1
2
1
8
1
16
1
32
1
64
1 half-life 2 half-lives 3 half-lives
1
2
1
4
1
8 1
16 1
32 1
64 1
128
Accumulating
“daughter”
isotopes
4 half-lives 5 half-lives 6 half-lives 7 half-lives
Surviving
“parent”
isotopes
Beginning

9. The iodine-131 nuclide has a half-life of 8 days. If you originally have a
625-g sample, after 2 months you will have approximately?
a. 40 g
b. 20 g
c. 10 g
d. 5 g
e. less than 1 g
625 g
312 g
156 g
78 g
39 g
20 g
10 g
5 g
2.5 g
1.25 g
0 d
8 d
16 d
24 d
32 d
40 d
48 d
56 d
64 d
72 d
0
1
2
3
4
5
6
7
8
9
Data Table: Half-life Decay
~ Amount Time # Half-Life
Assume 30 days = 1 month
60 days
8 days
= 7.5 half-lives
N = No(1/2)n
N = amount remaining
No = original amount
n = # of half-lives
N = (625 g)(1/2)7.5
N = 3.45 g

10. ln 2
Given that the half-life of carbon-14 is 5730 years, consider a
sample of fossilized wood that, when alive, would have contained 24 g
of carbon-14. It now contains 1.5 g of carbon-14.
How old is the sample?
24 g
12 g
6 g
3 g
1.5 g
0 y
5,730 y
11,460 y
17,190 y
22,920 y
0
1
2
3
4
Data Table: Half-life Decay
Amount Time # Half-Life
ln = - k tN
No
t1/2 =
0.693
k
5730 y =
0.693
k
k = 1.209 x 10-4
ln = - (1.209x10-4) t1.5 g
24 g
t = 22,933 years

11. Half-Life Practice Calculations
• The half-life of carbon-14 is 5730 years. If a sample originally contained 3.36 g of
C-14, how much is present after 22,920 years?
• Gold-191 has a half-life of 12.4 hours. After one day and 13.2 hours, 10.6 g of
gold-19 remains in a sample. How much gold-191 was originally present in the
sample?
• There are 3.29 g of iodine-126 remaining in a sample originally containing 26.3 g of
iodine-126. The half-life of iodine-126 is 13 days. How old is the sample?
• A sample that originally contained 2.5 g of rubidium-87 now contains 1.25 g. The
half-life of rubidium-87 is 6 x 1010 years. How old is the sample? Is this possible?
Why or why not?
0.21 g C-14
84.8 g Au-191
39 days old
6 x 1010 years
(60 billion years old)

12. 22,920 years
The half-life of carbon-14 is 5730 years. If a sample originally contained
3.36 g of C-14, how much is present after 22,920 years?
3.36 g
1.68 g
0.84 g
0.42 g
0.21 g
0 y
5,730 y
11,460 y
17,190 y
22,920 y
0
1
2
3
4
Data Table: Half-life Decay
Amount Time # Half-Lifet1/2 = 5730 years
n =
5,730 years
n = 4 half-lives
(4 half-lives)(5730 years) = age of sample
(# of half-lives)(half-life) = age of sample
22,920 years