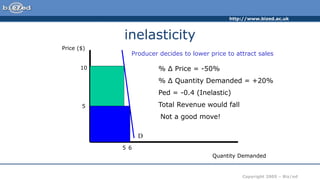
The document discusses methods for determining the elasticity of demand, specifically the total revenue method. It explains that demand is elastic when total revenue moves in the opposite direction of a price change, and inelastic when total revenue moves in the same direction. An example is provided to illustrate determining elasticity using the total revenue method. Additionally, the midpoint method for calculating elasticity is introduced as a more accurate approach.