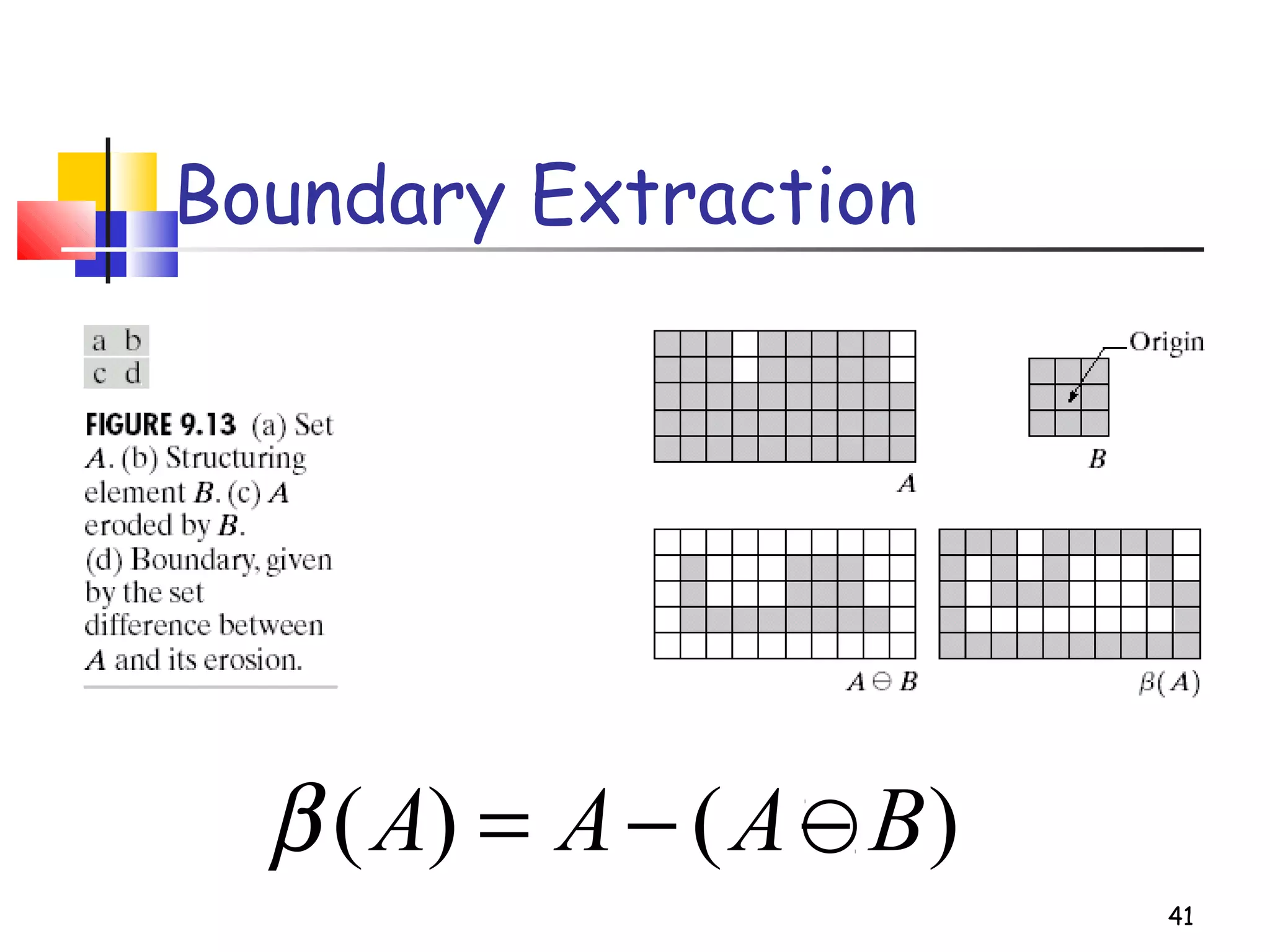
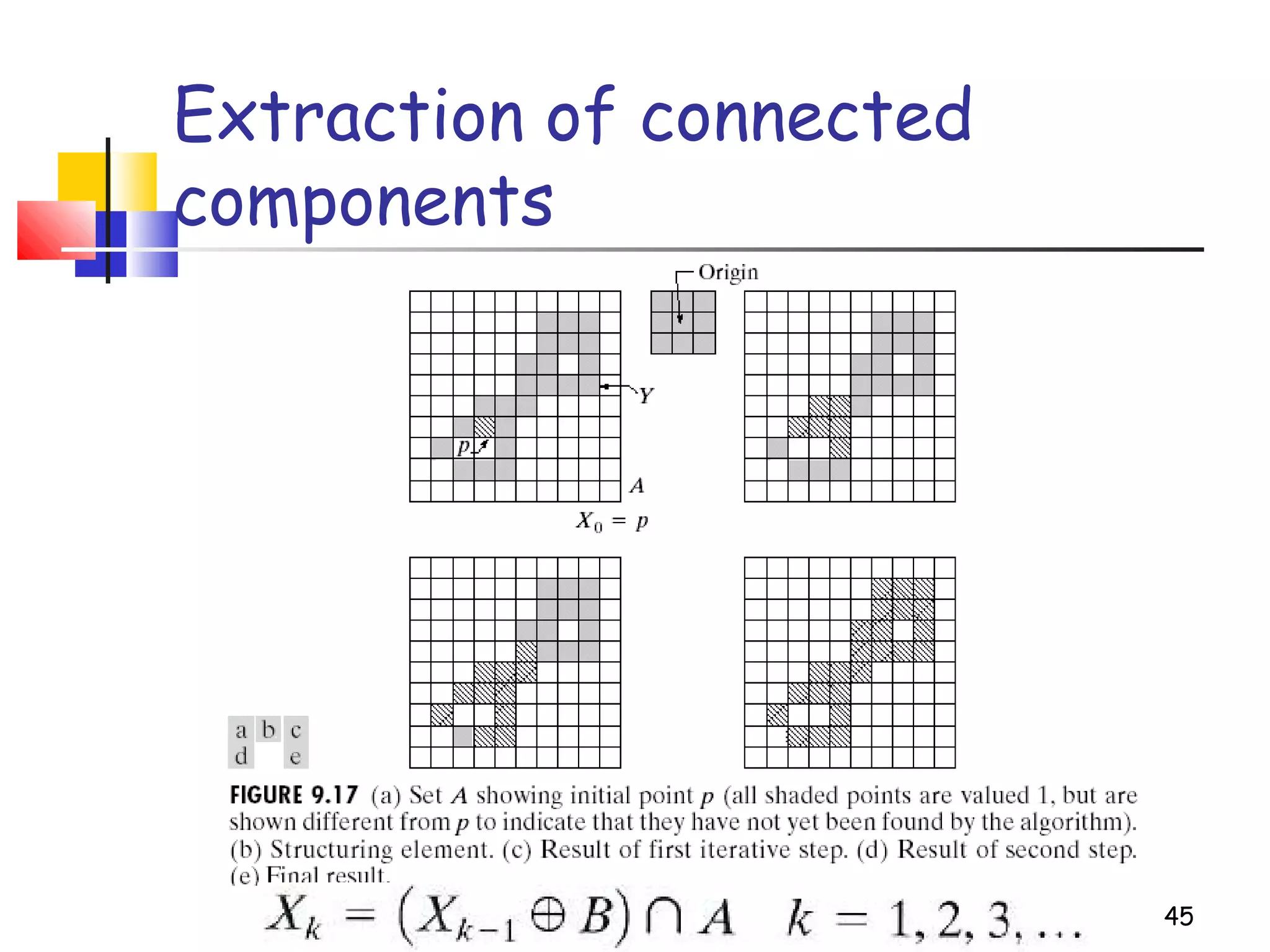
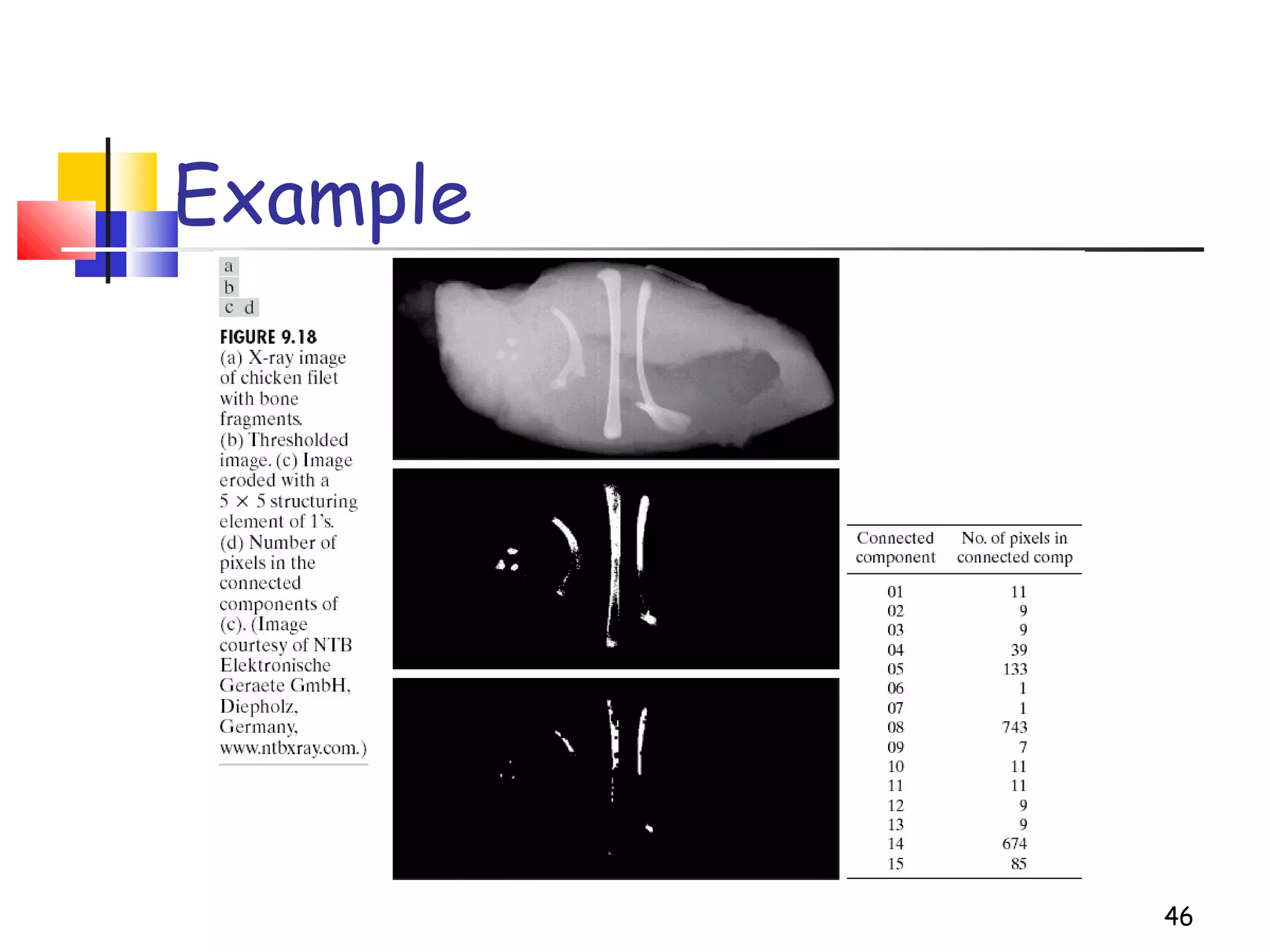
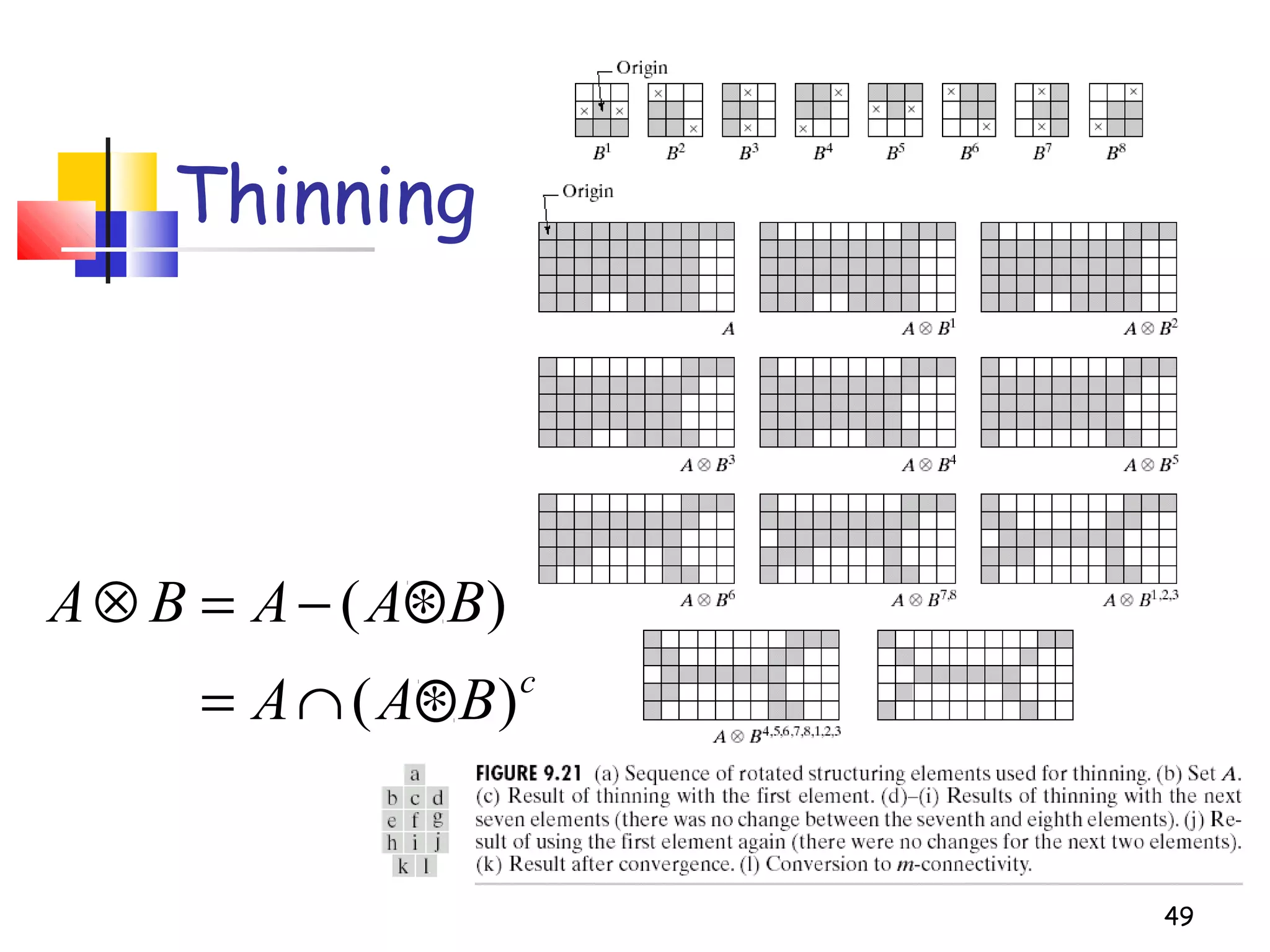
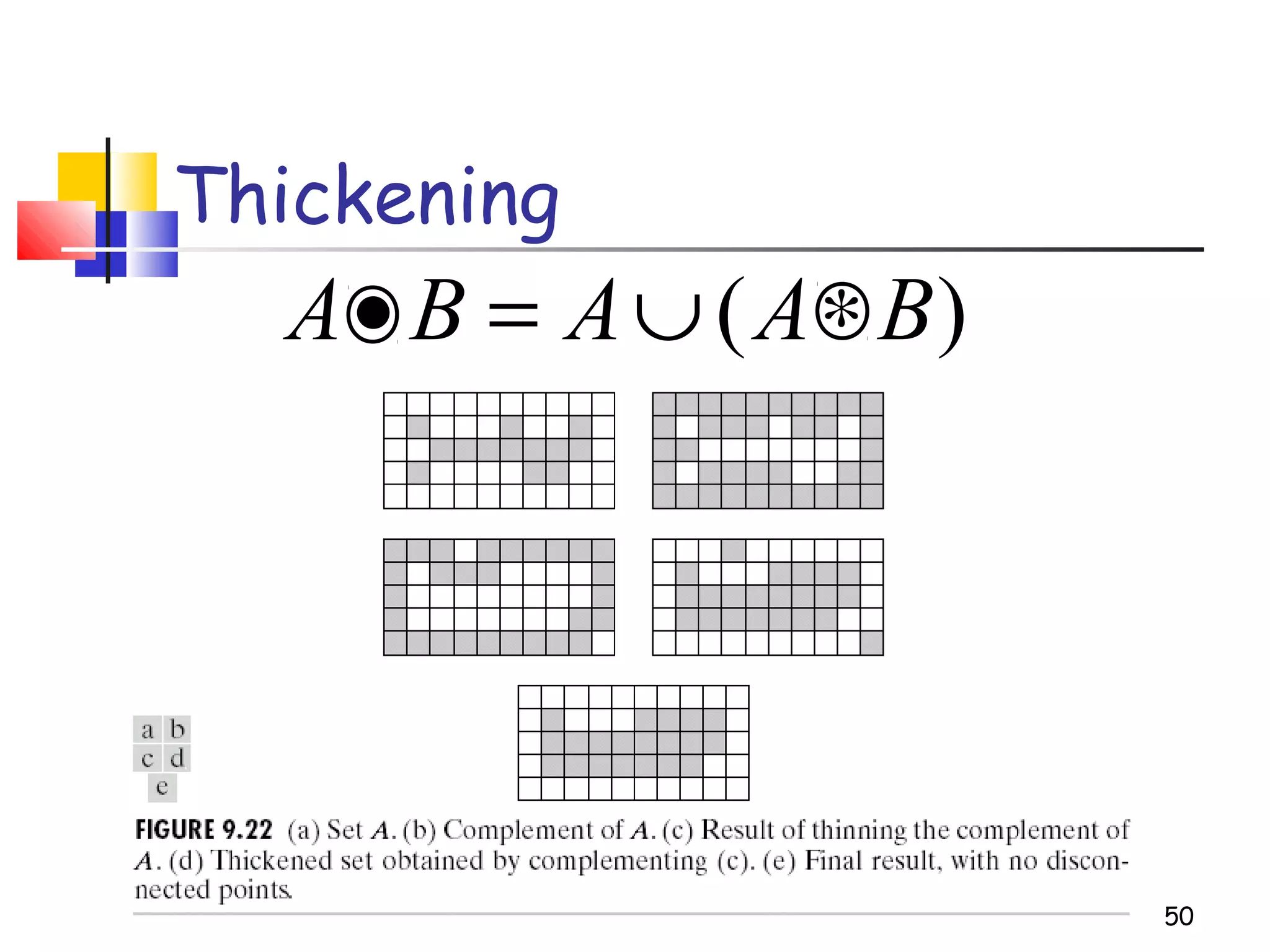
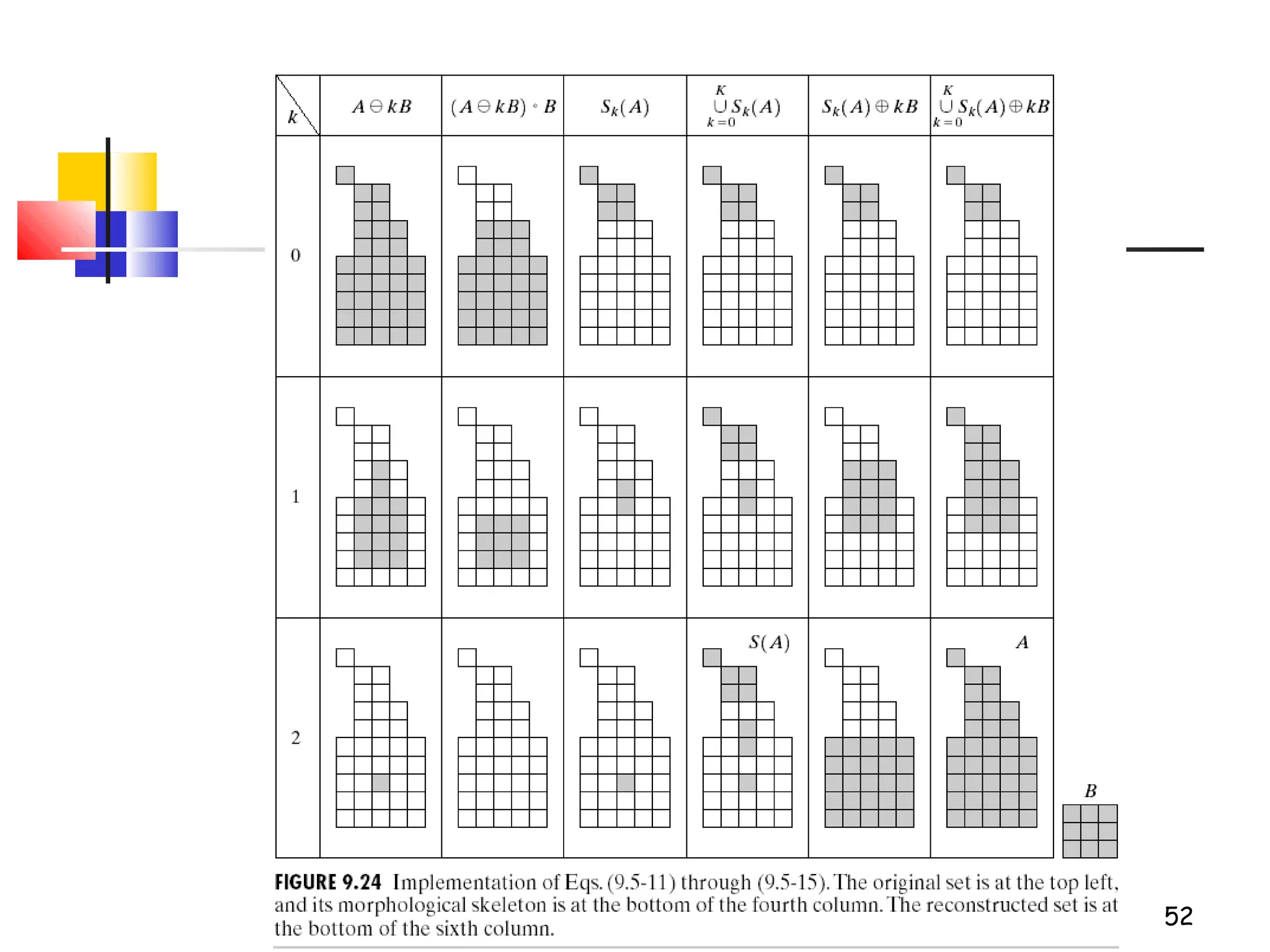
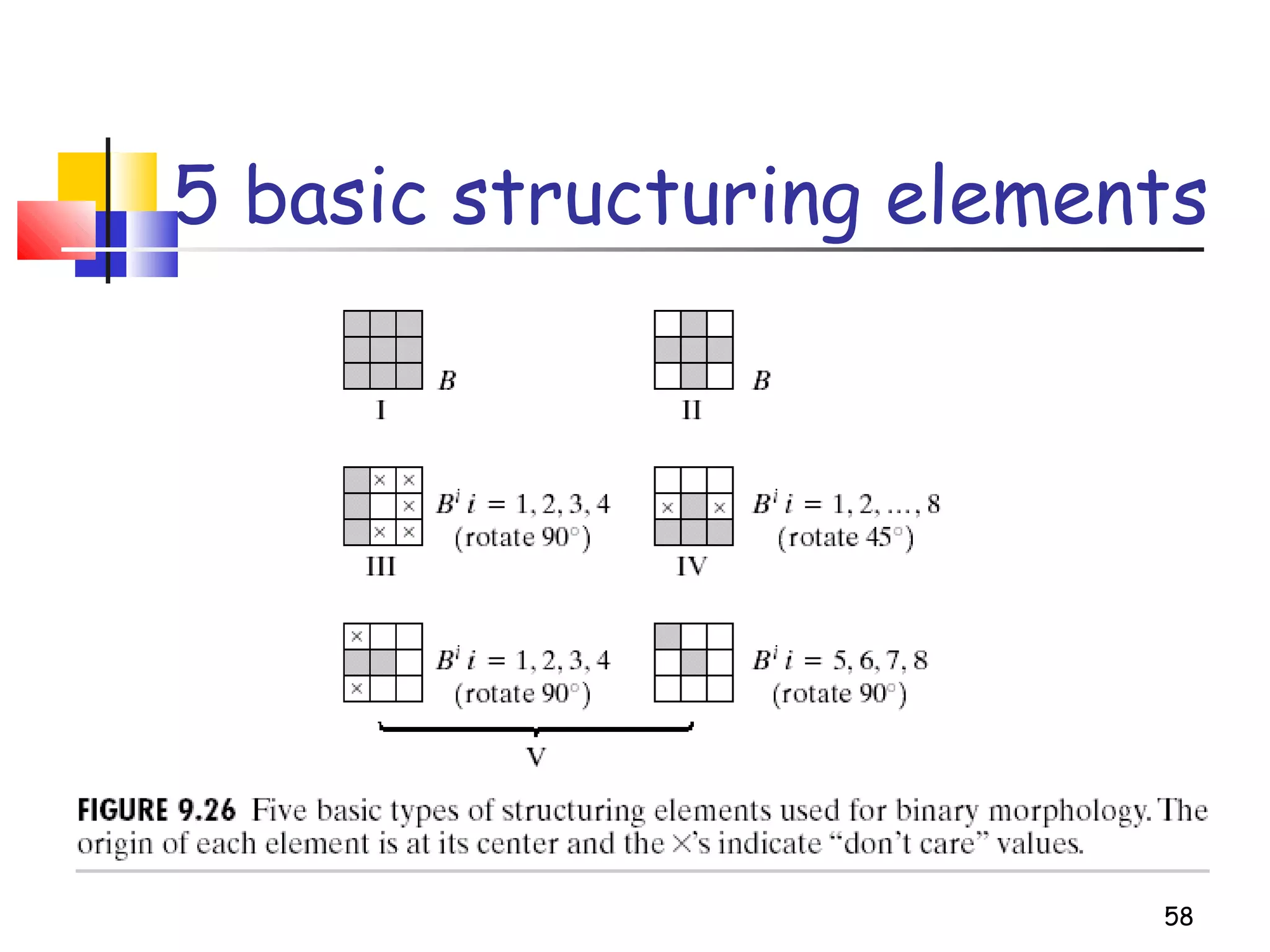
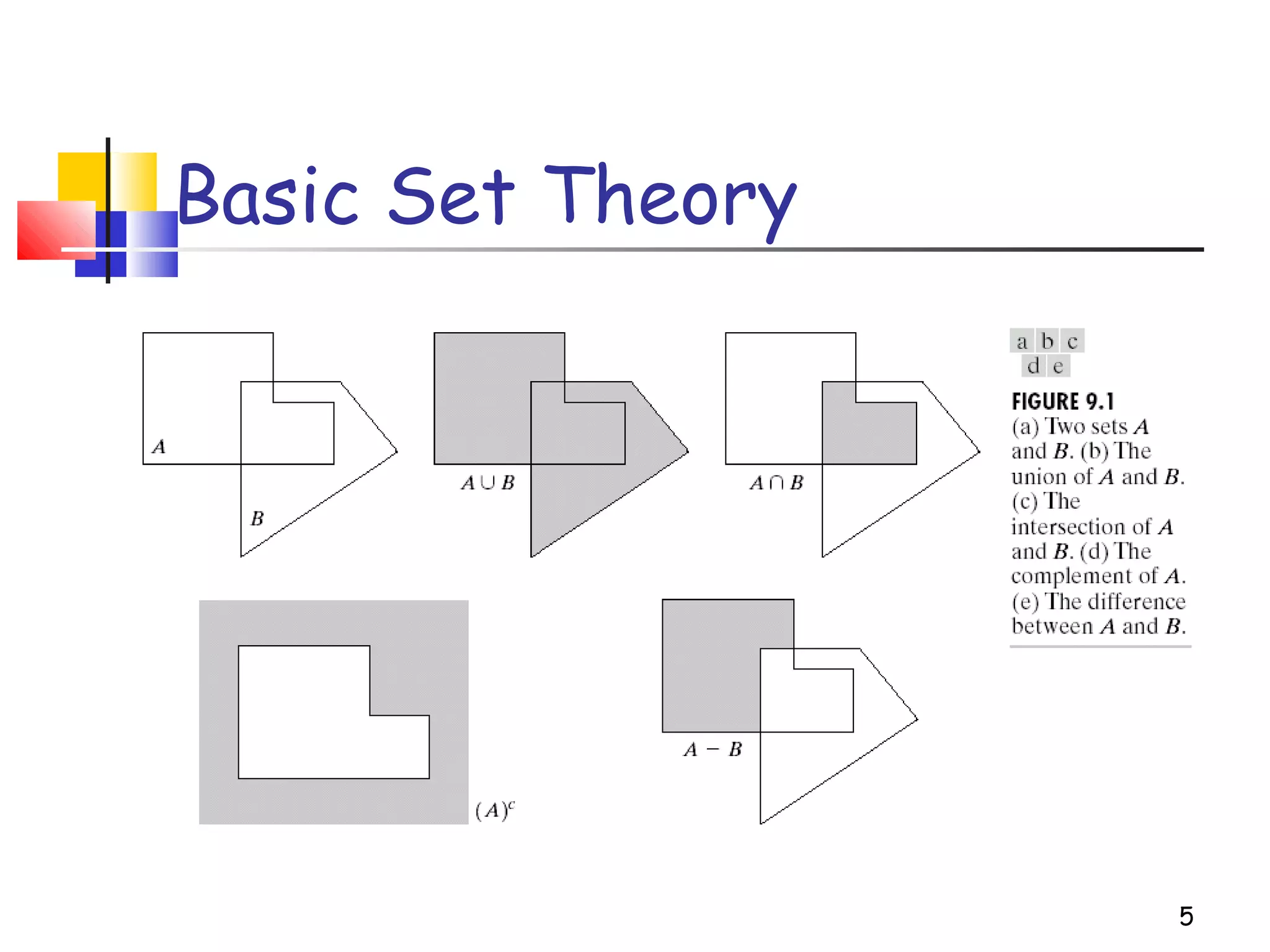
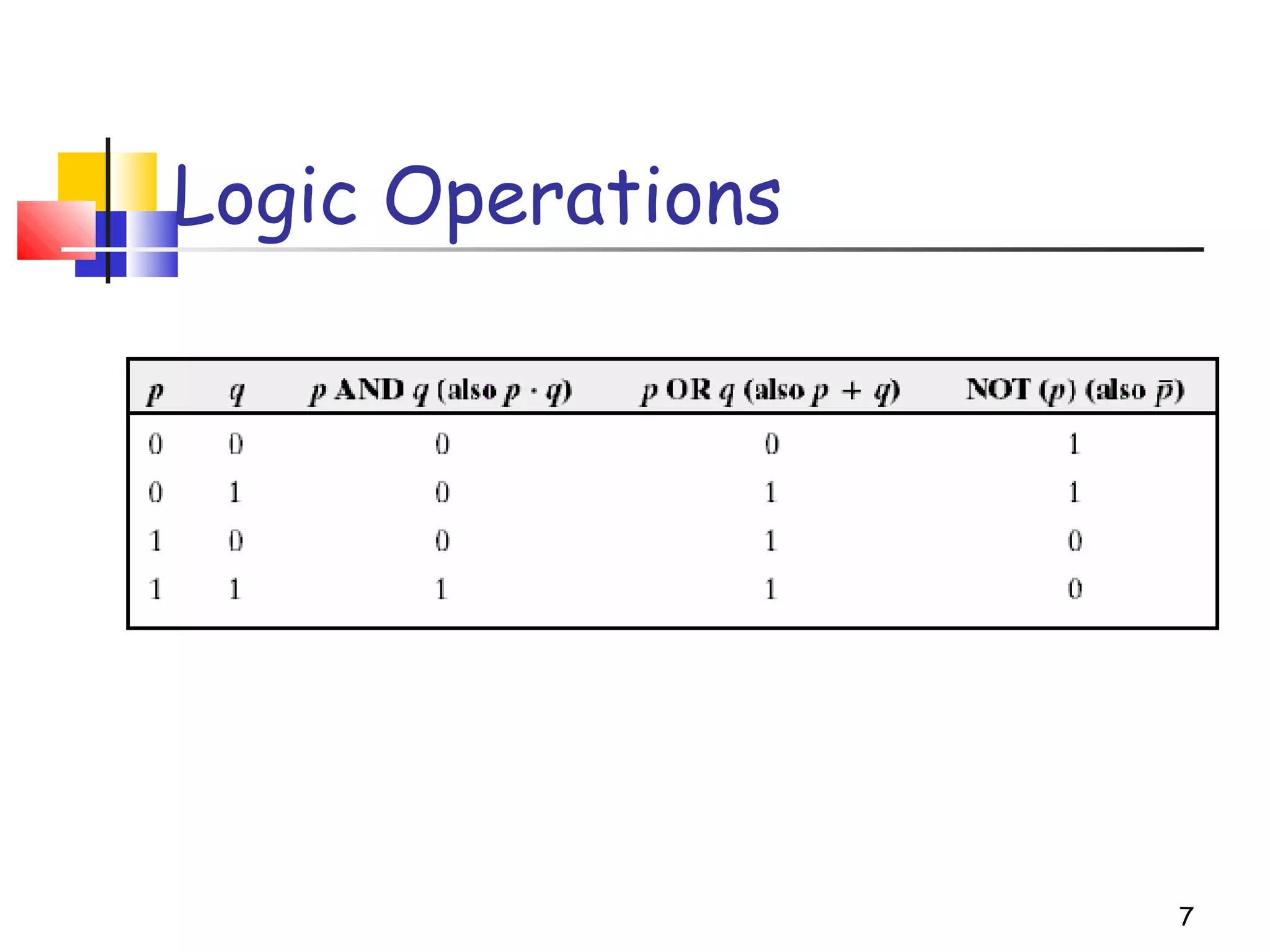
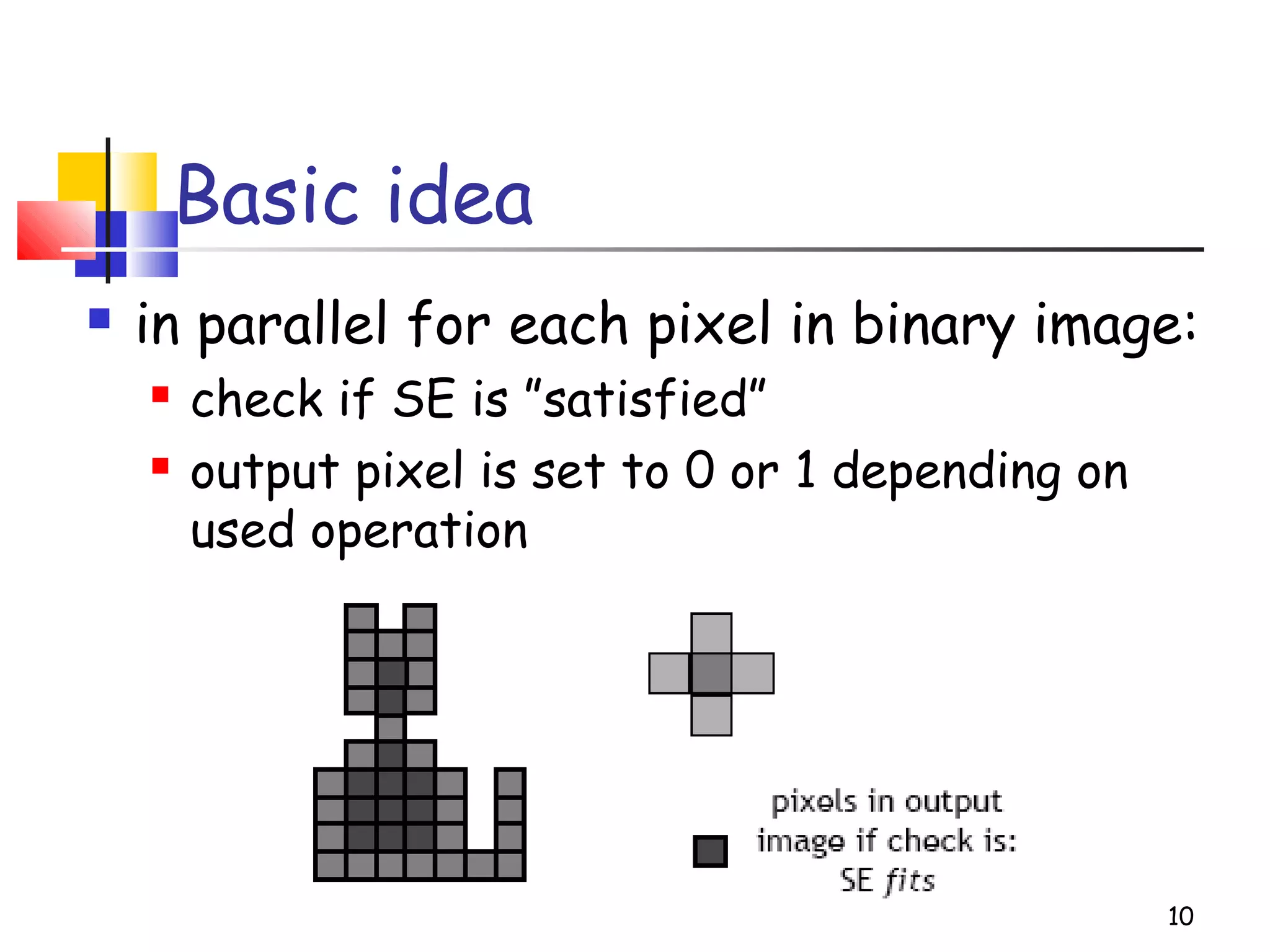
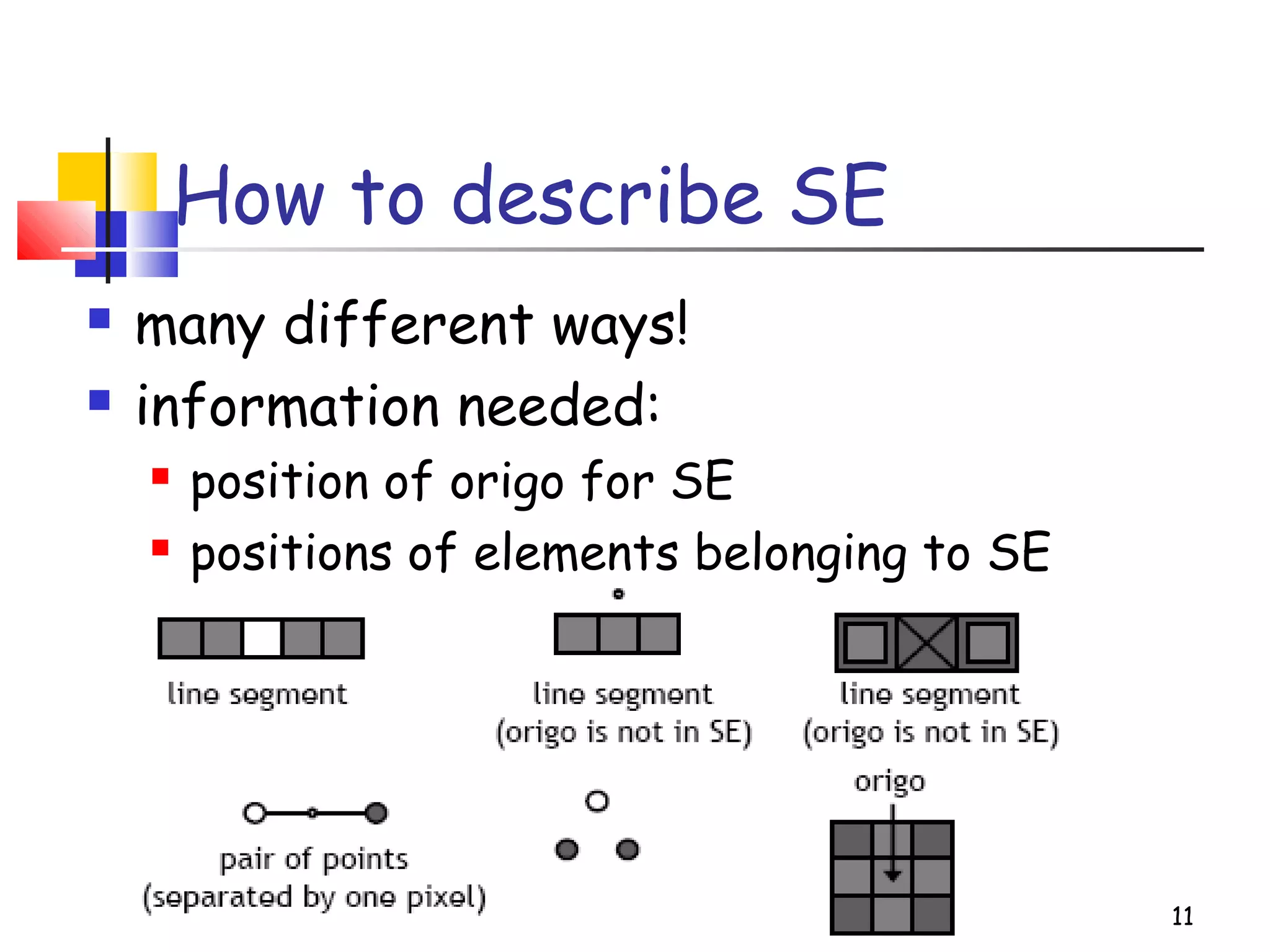
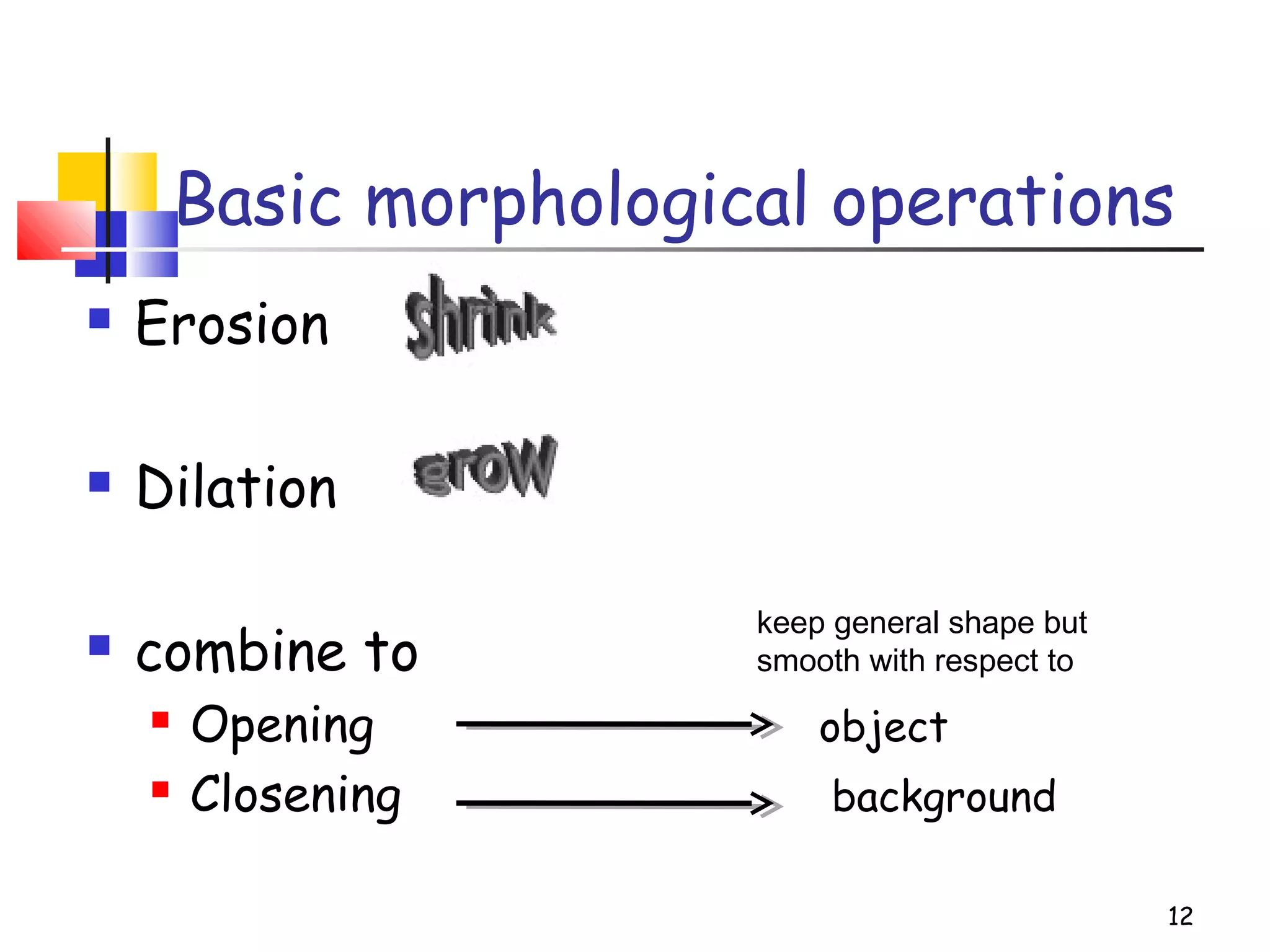
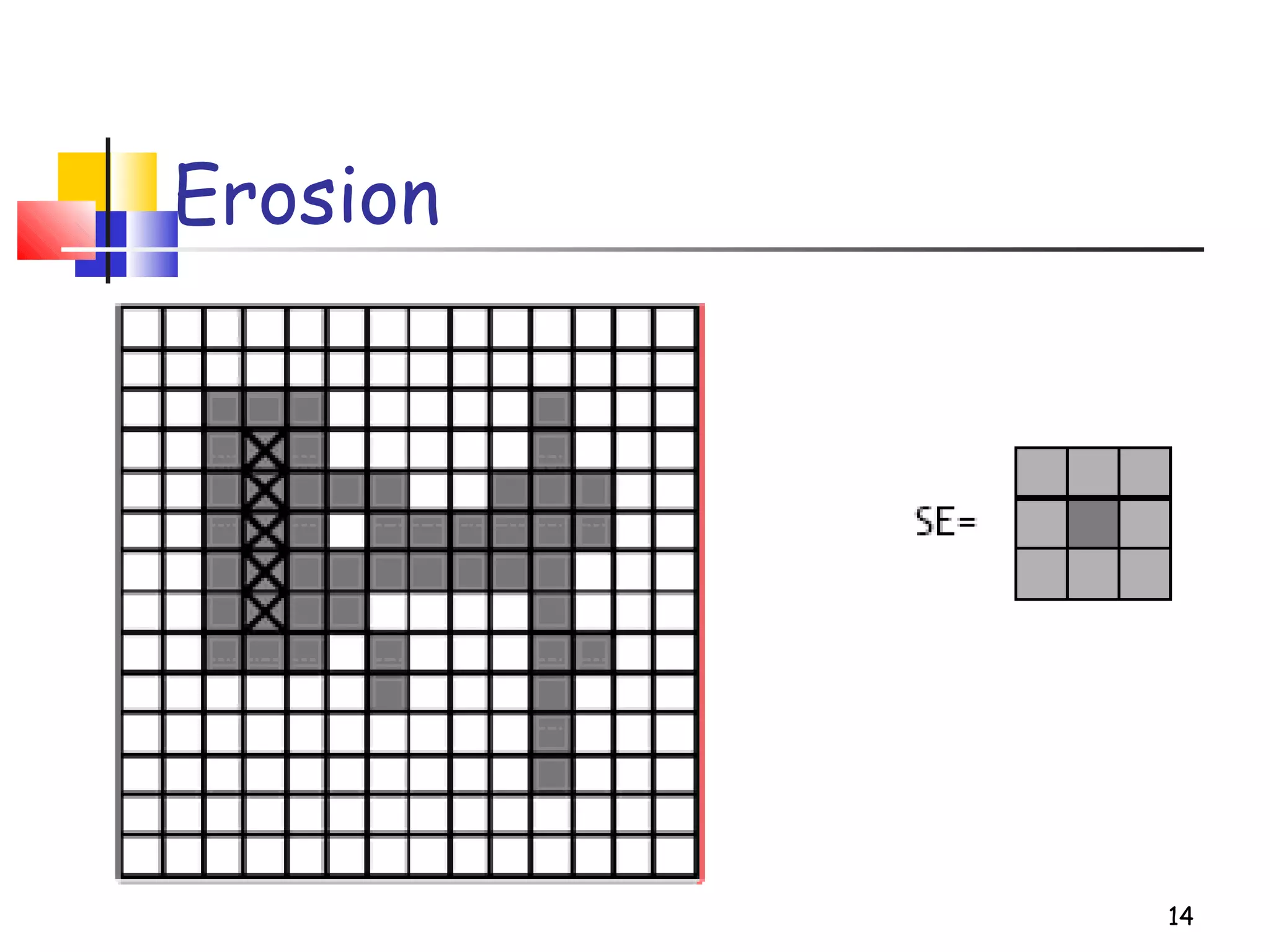
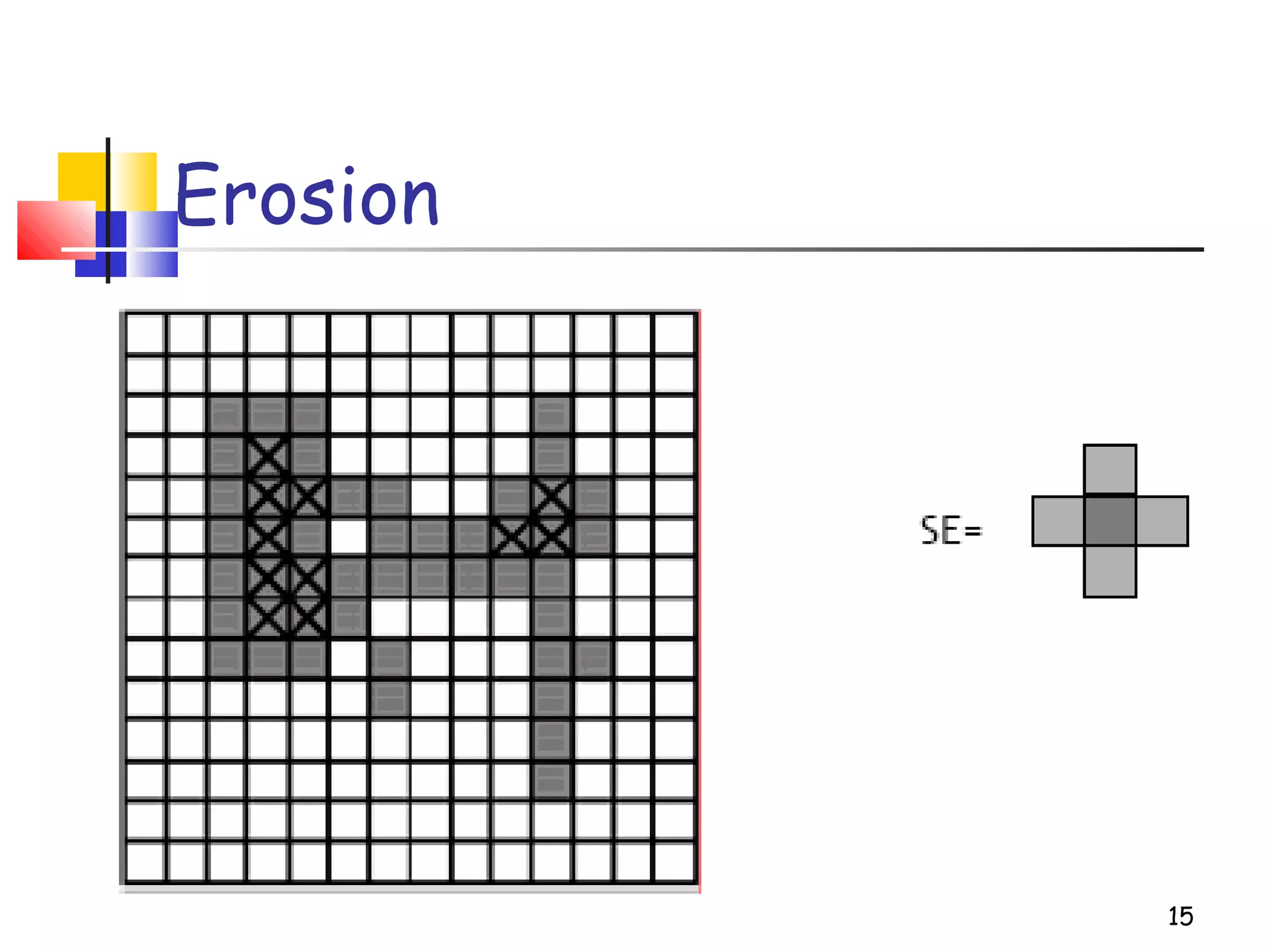
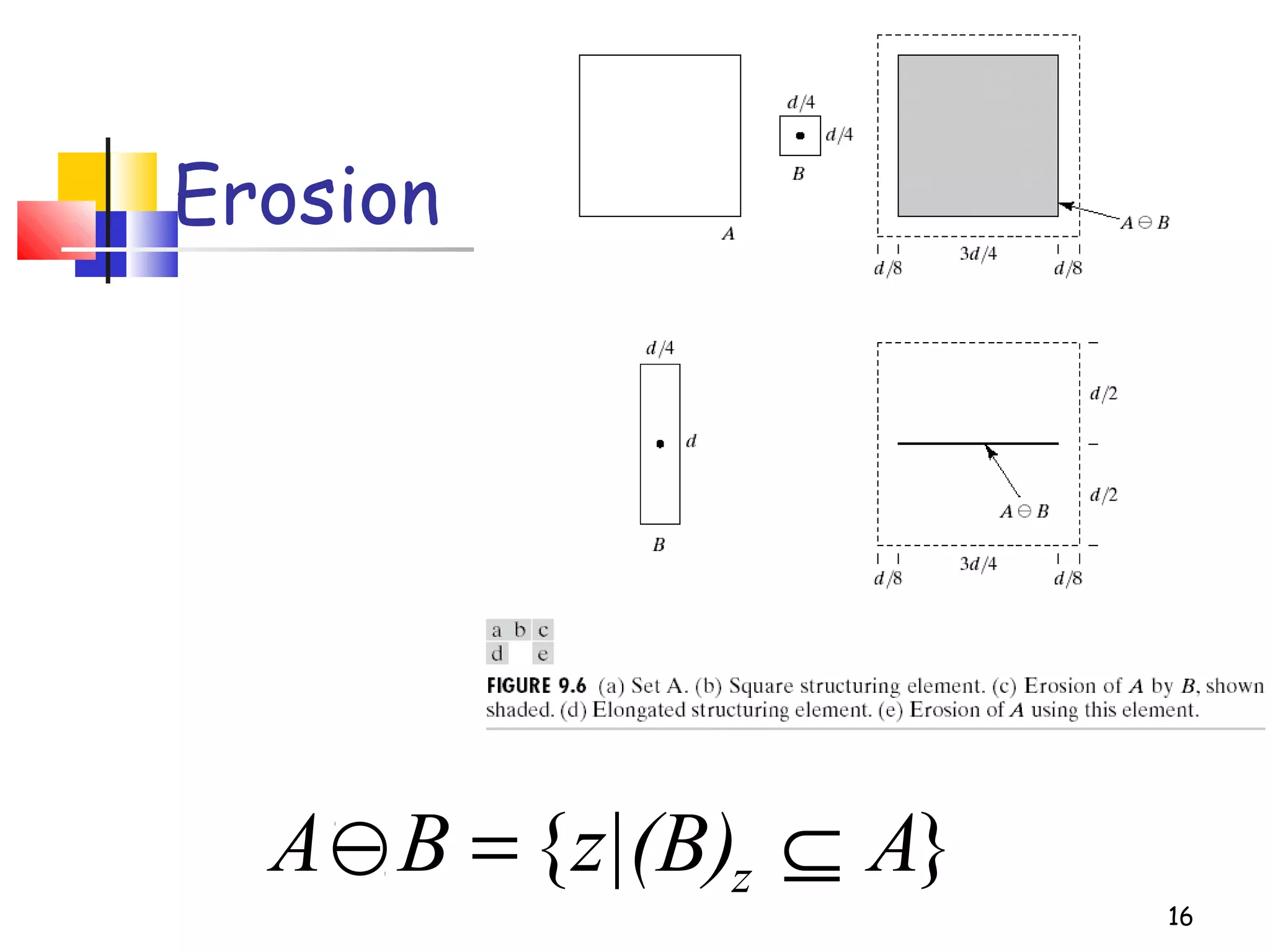
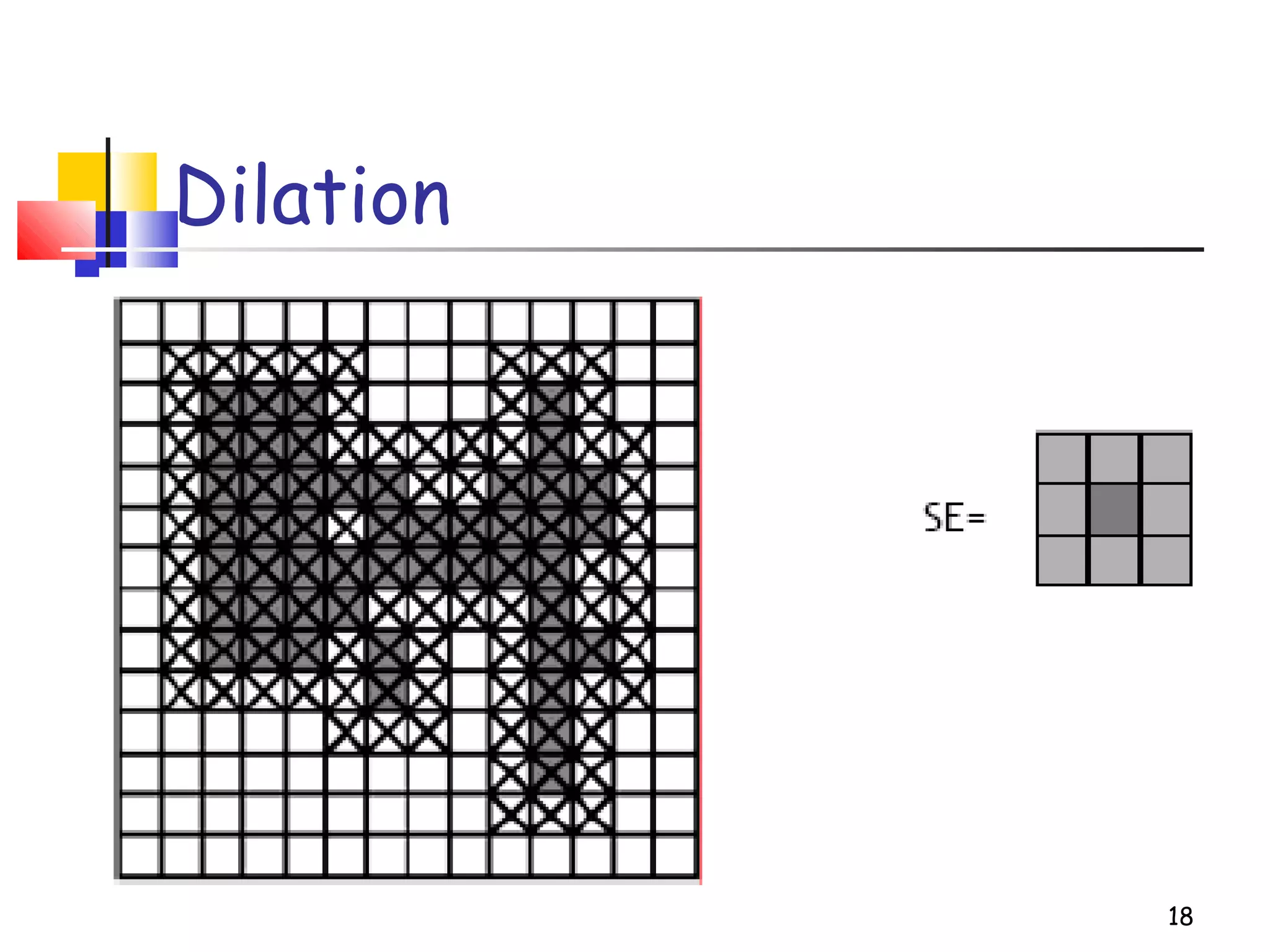
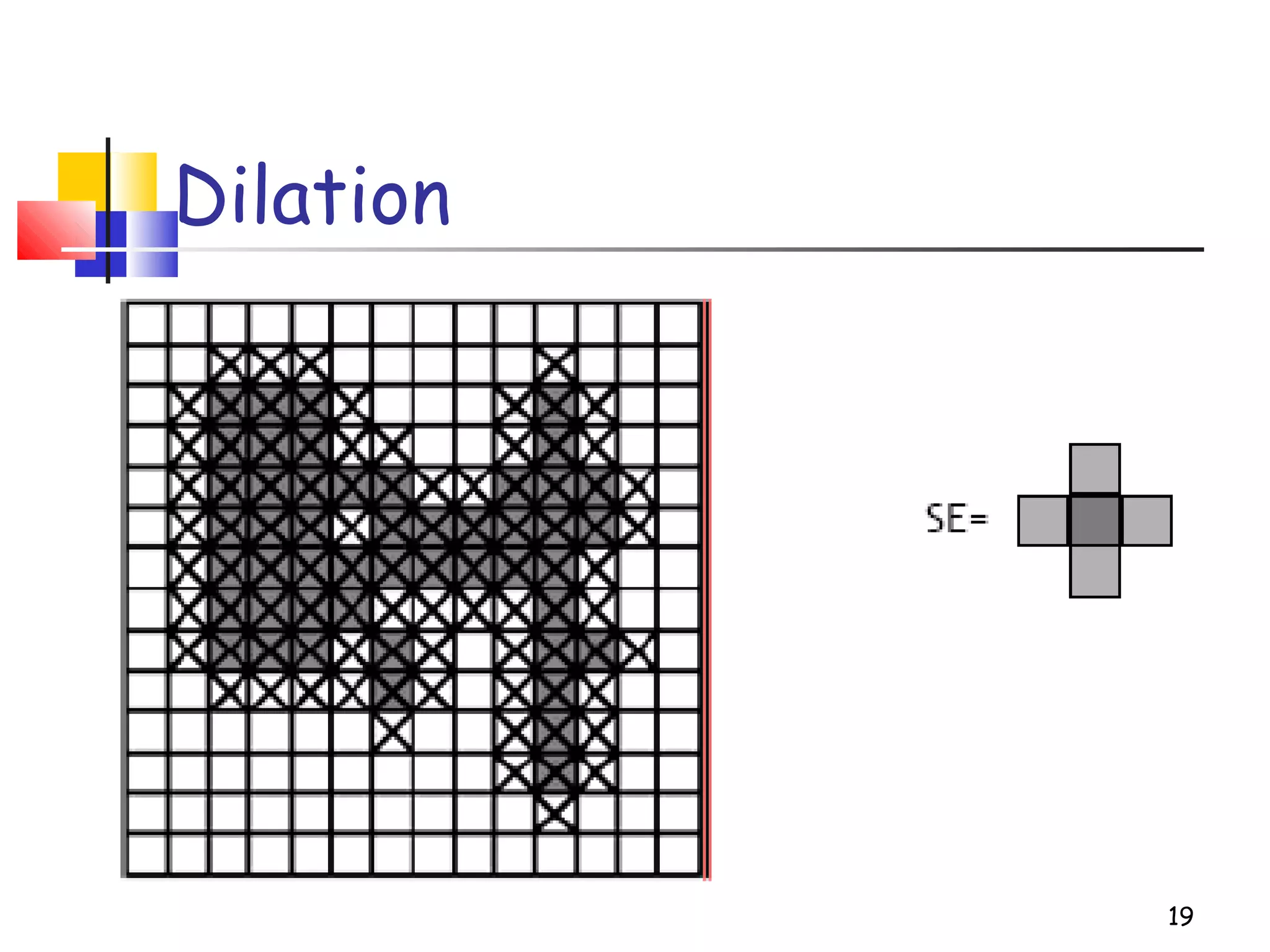
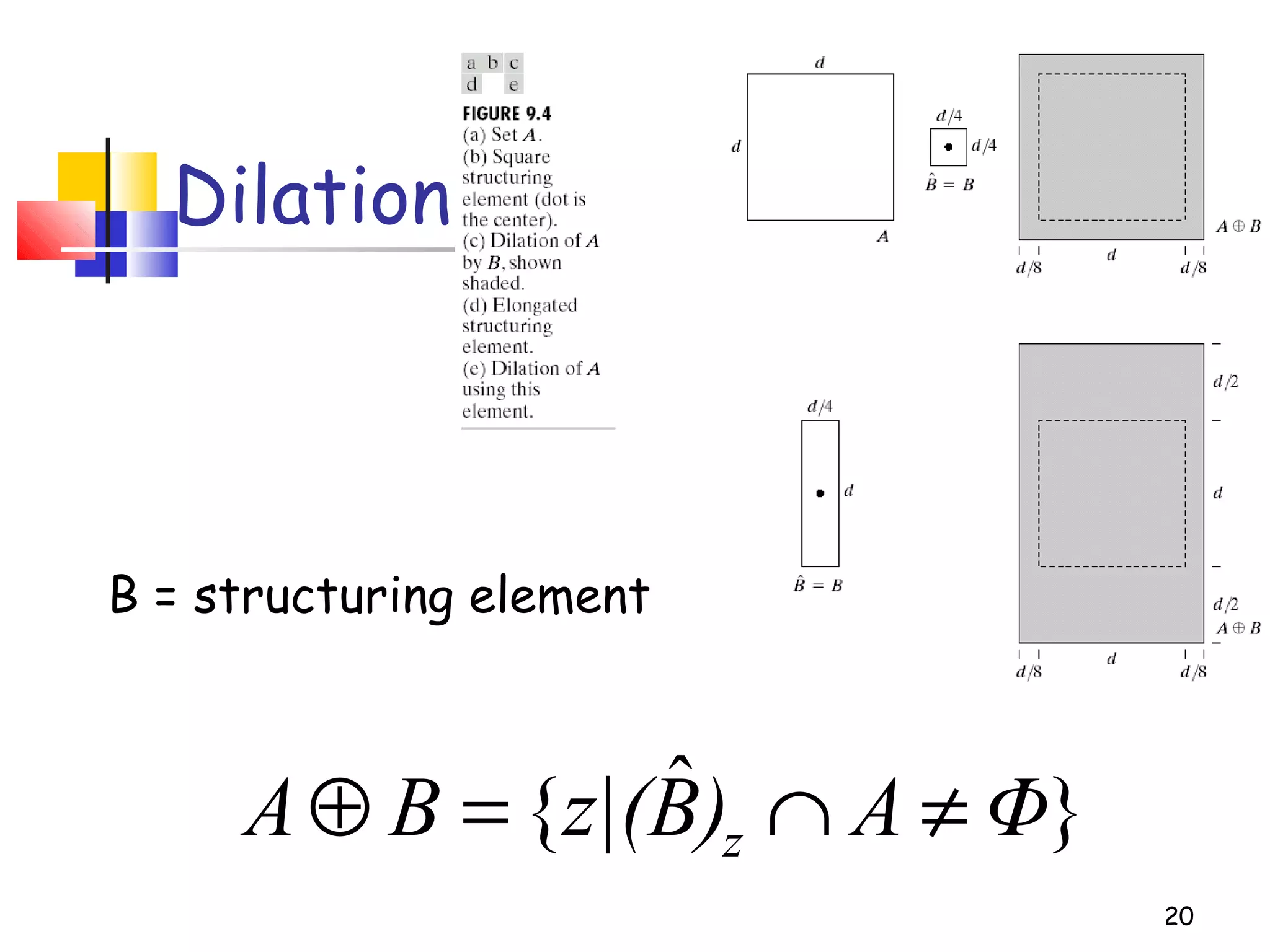
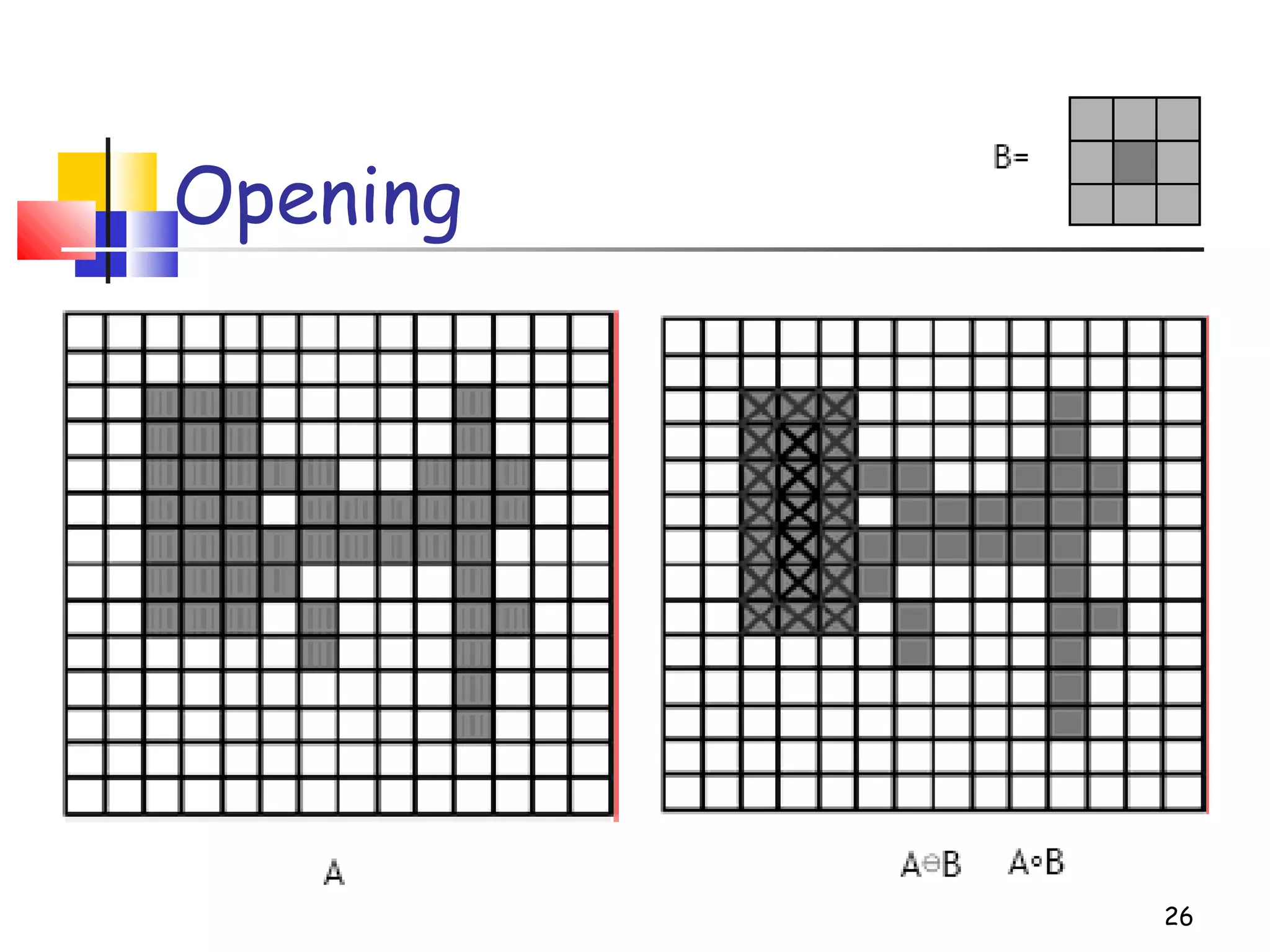
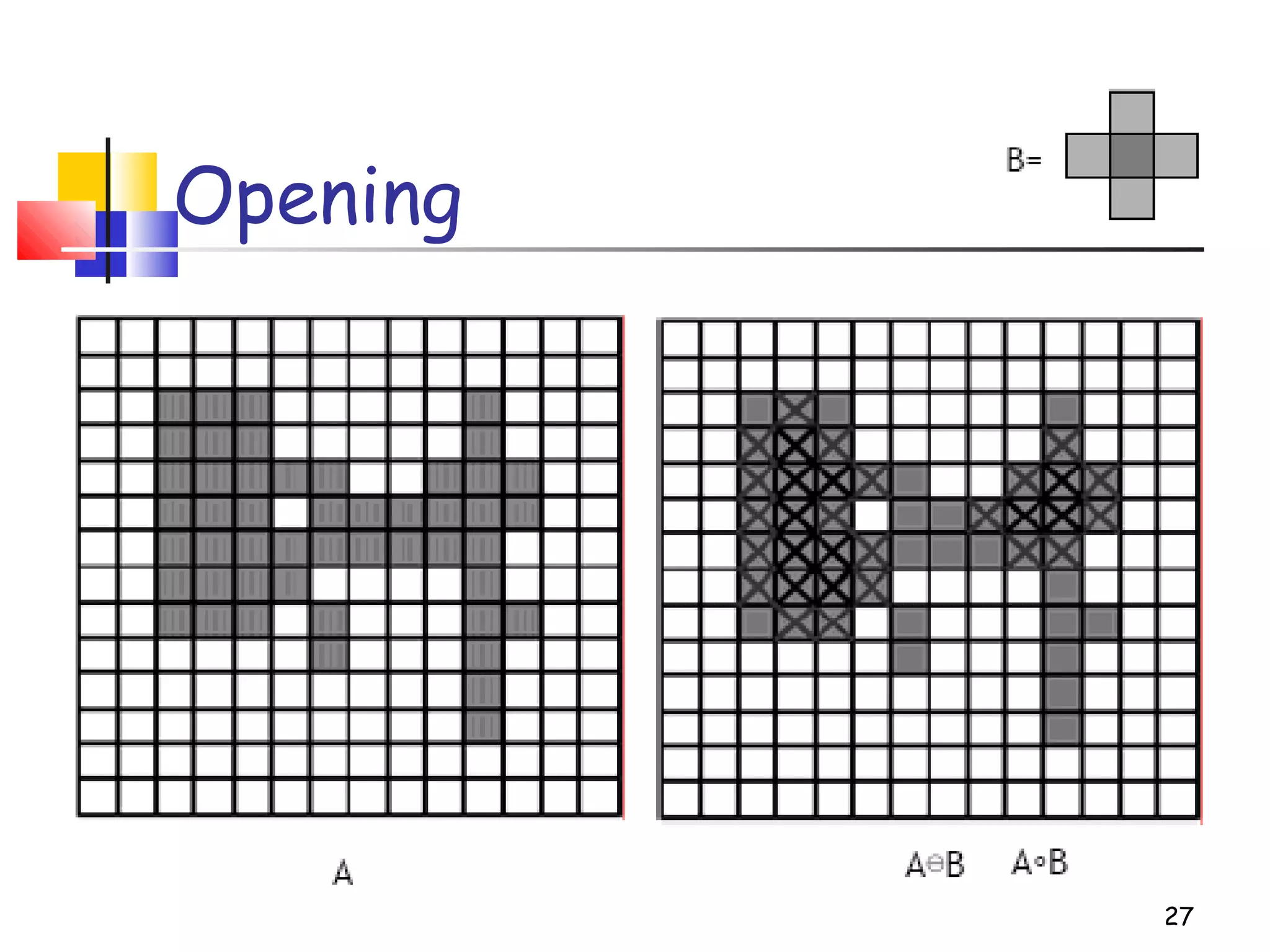
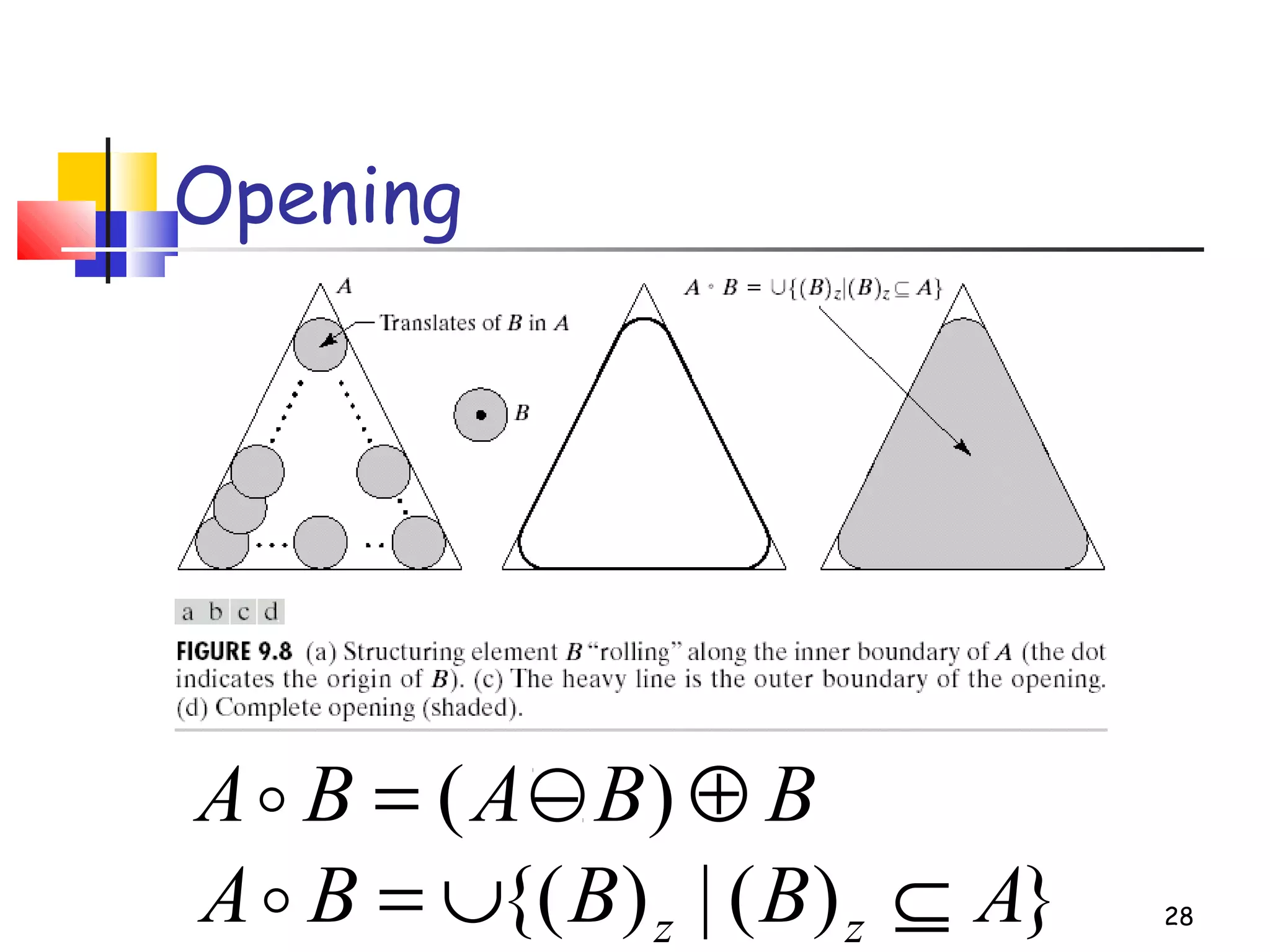
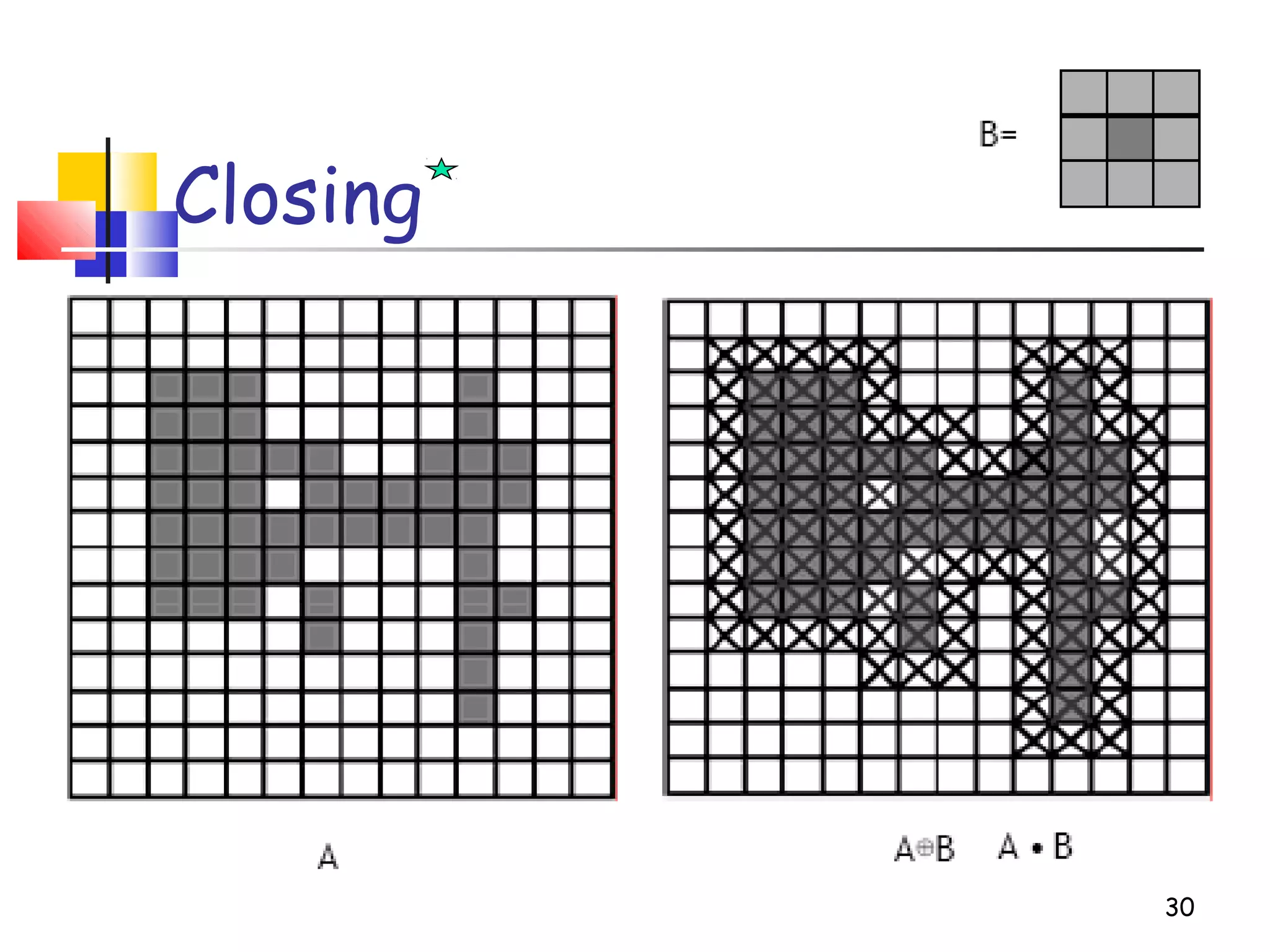
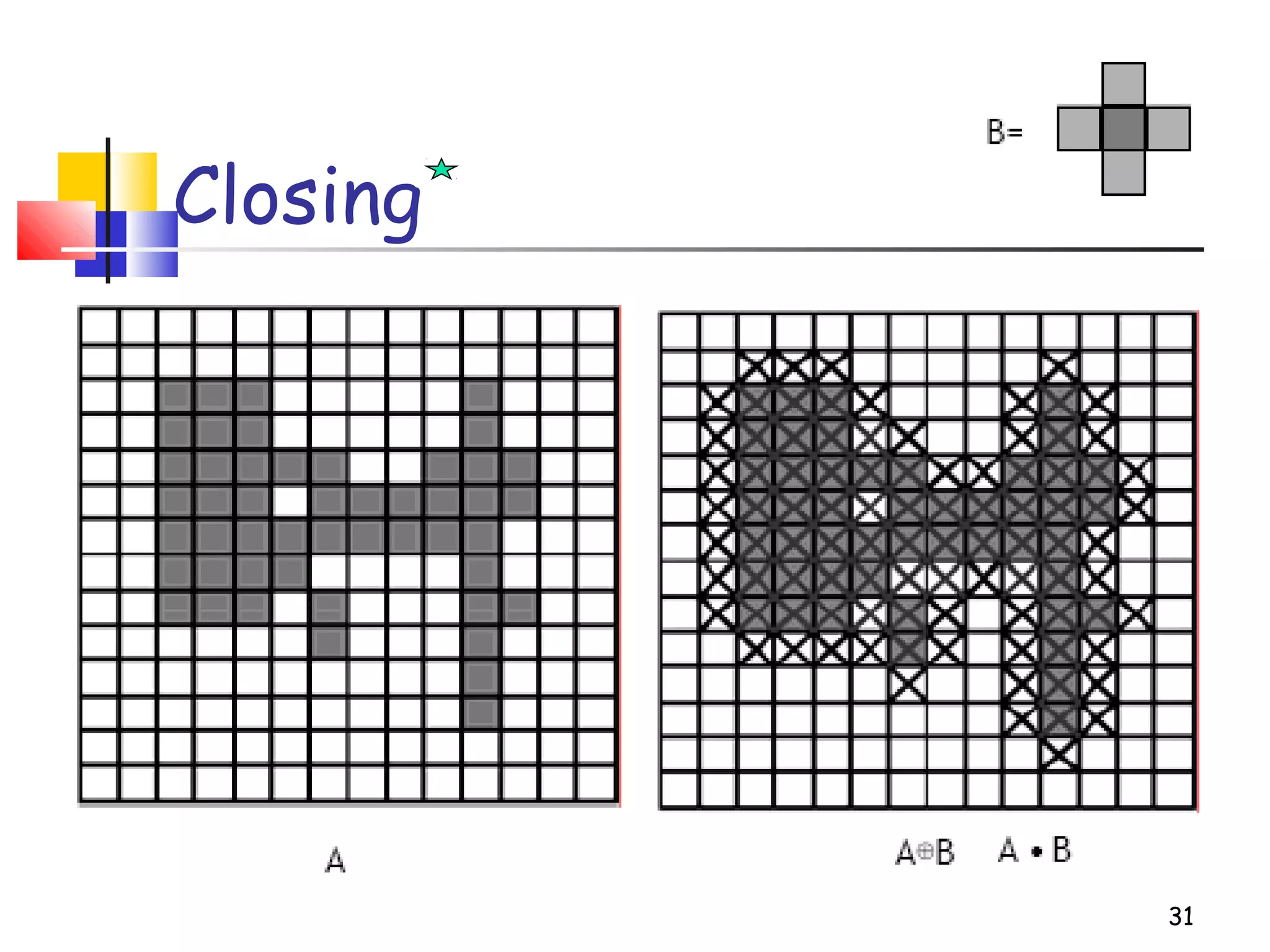
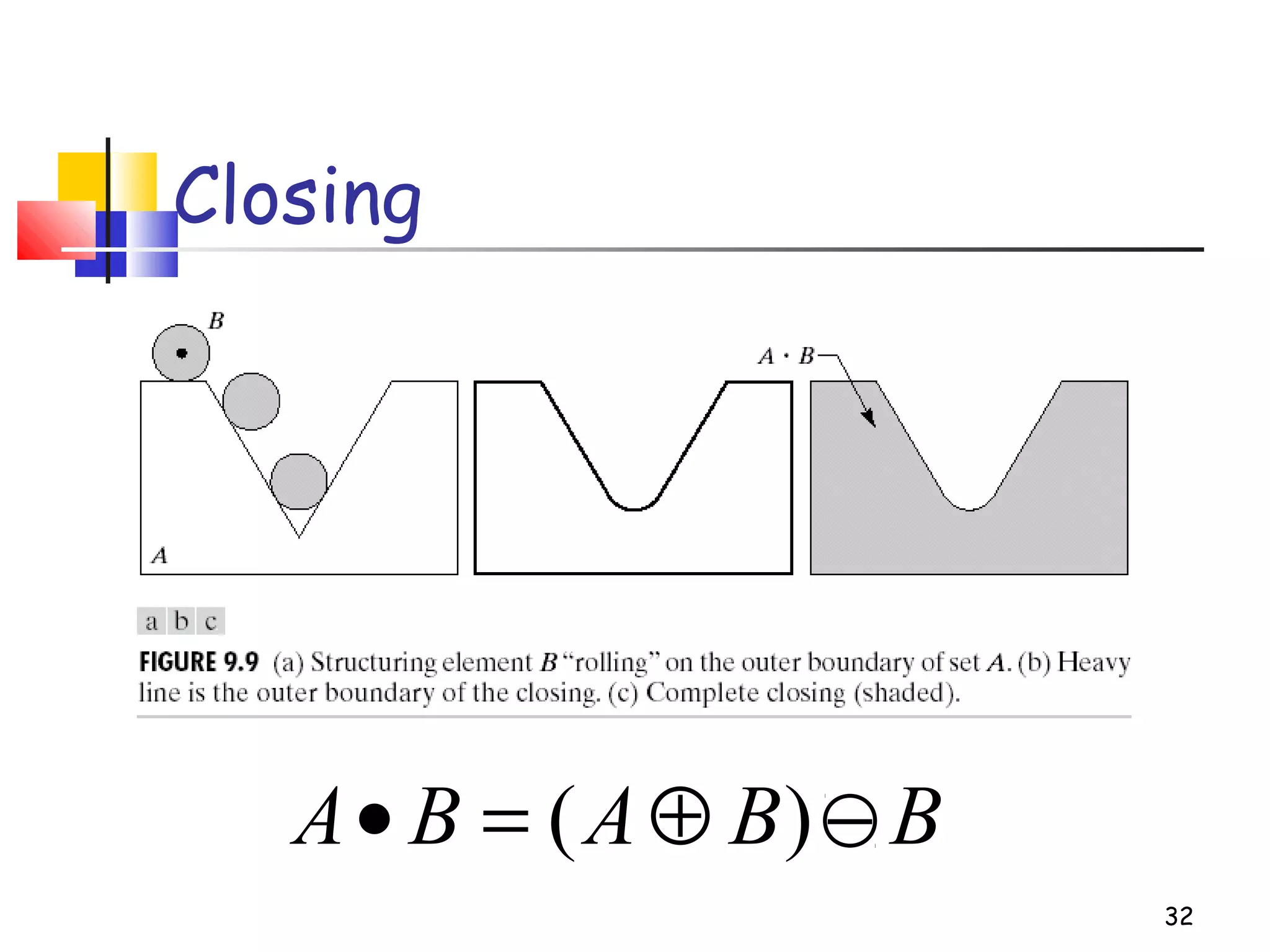
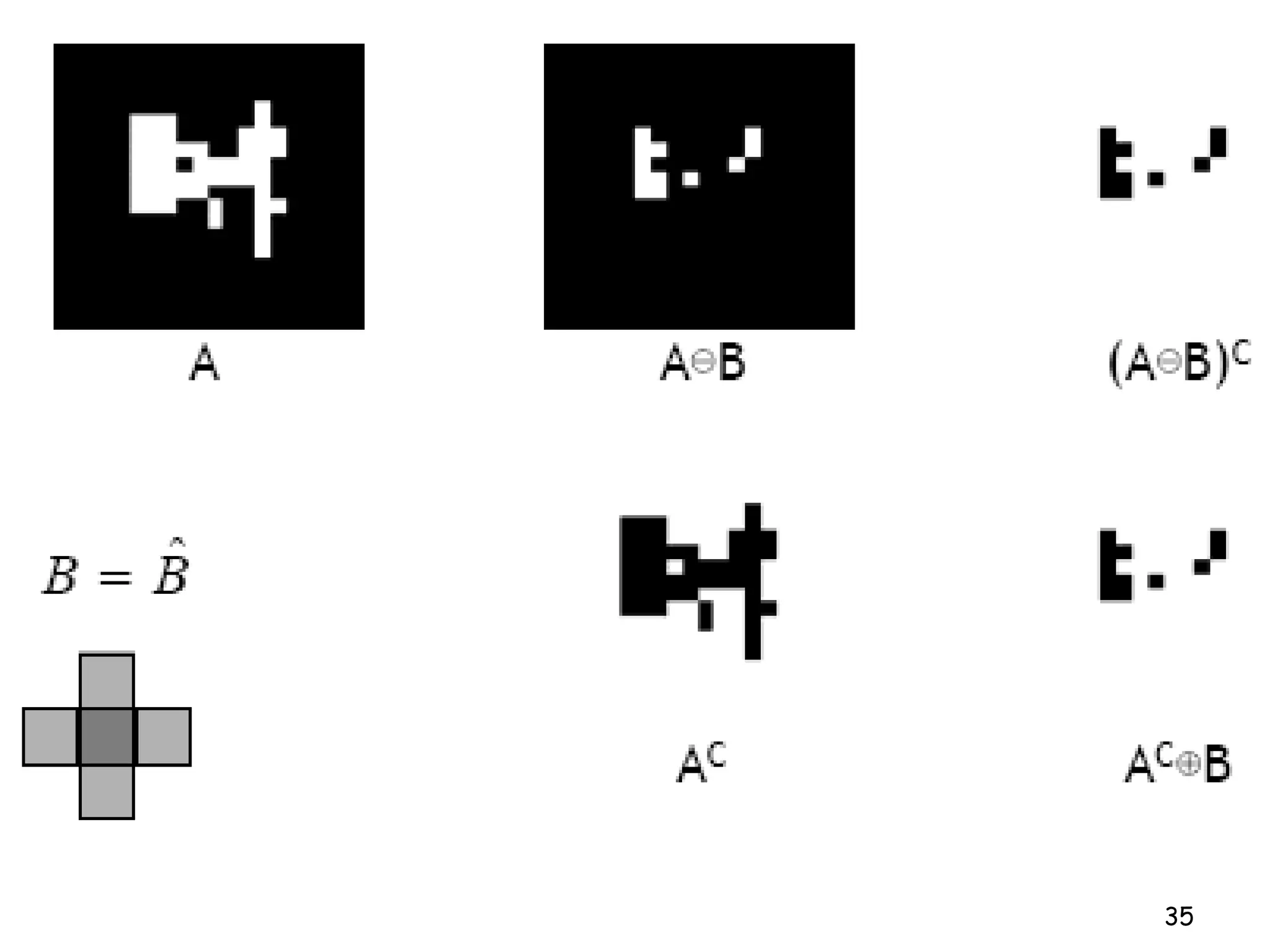
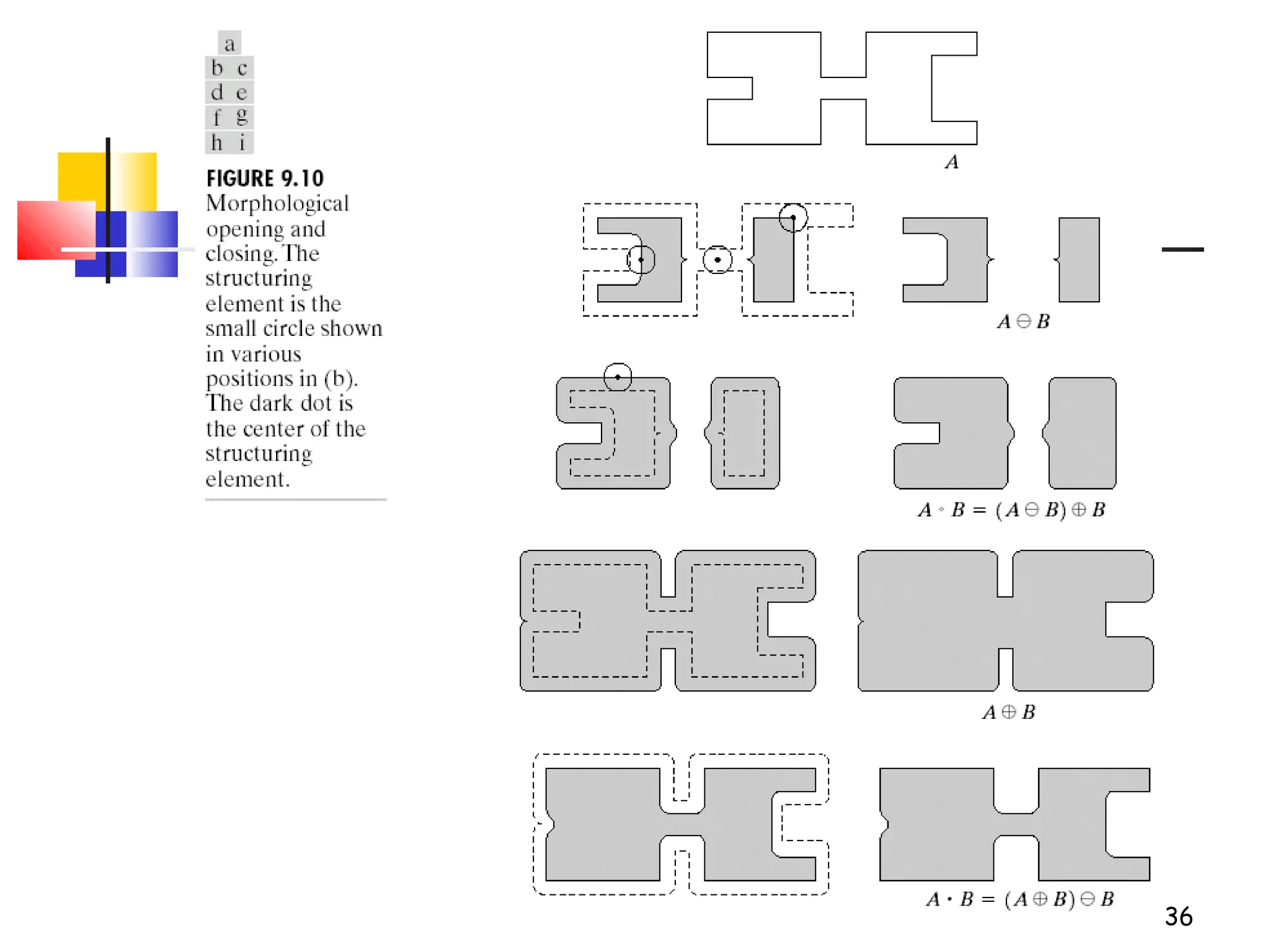
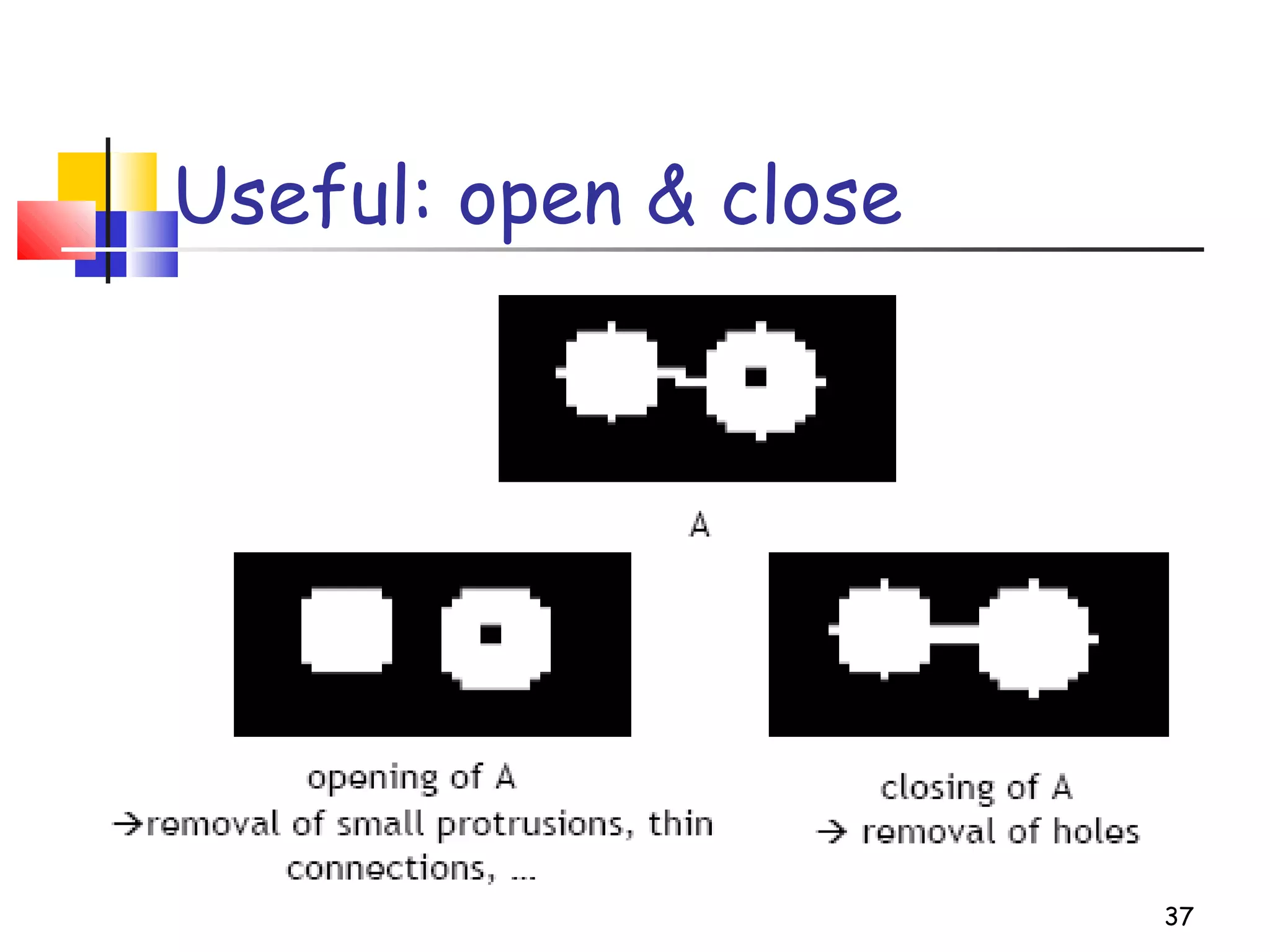
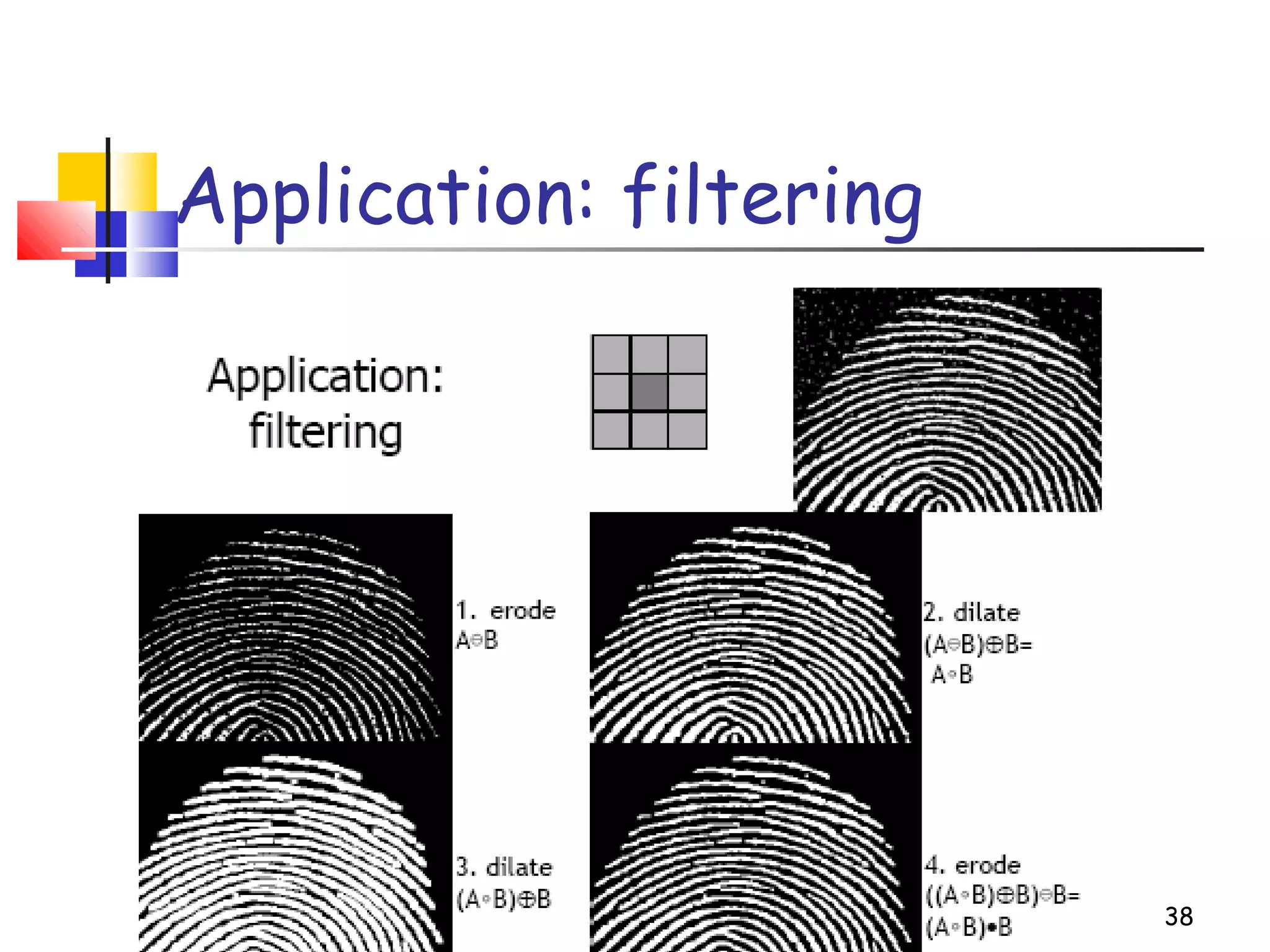
Mathematical morphology is a framework for image analysis using set theory operations. It is used for tasks like noise filtering, shape analysis, and segmentation. Basic operations include erosion, dilation, opening, and closing using a structuring element. Erosion shrinks objects while dilation expands them. Opening eliminates small objects and closing fills small holes. Together these operations can filter images while preserving overall shapes. Morphological operations also enable extracting object boundaries, thinning images to skeletons, and finding connected components.

















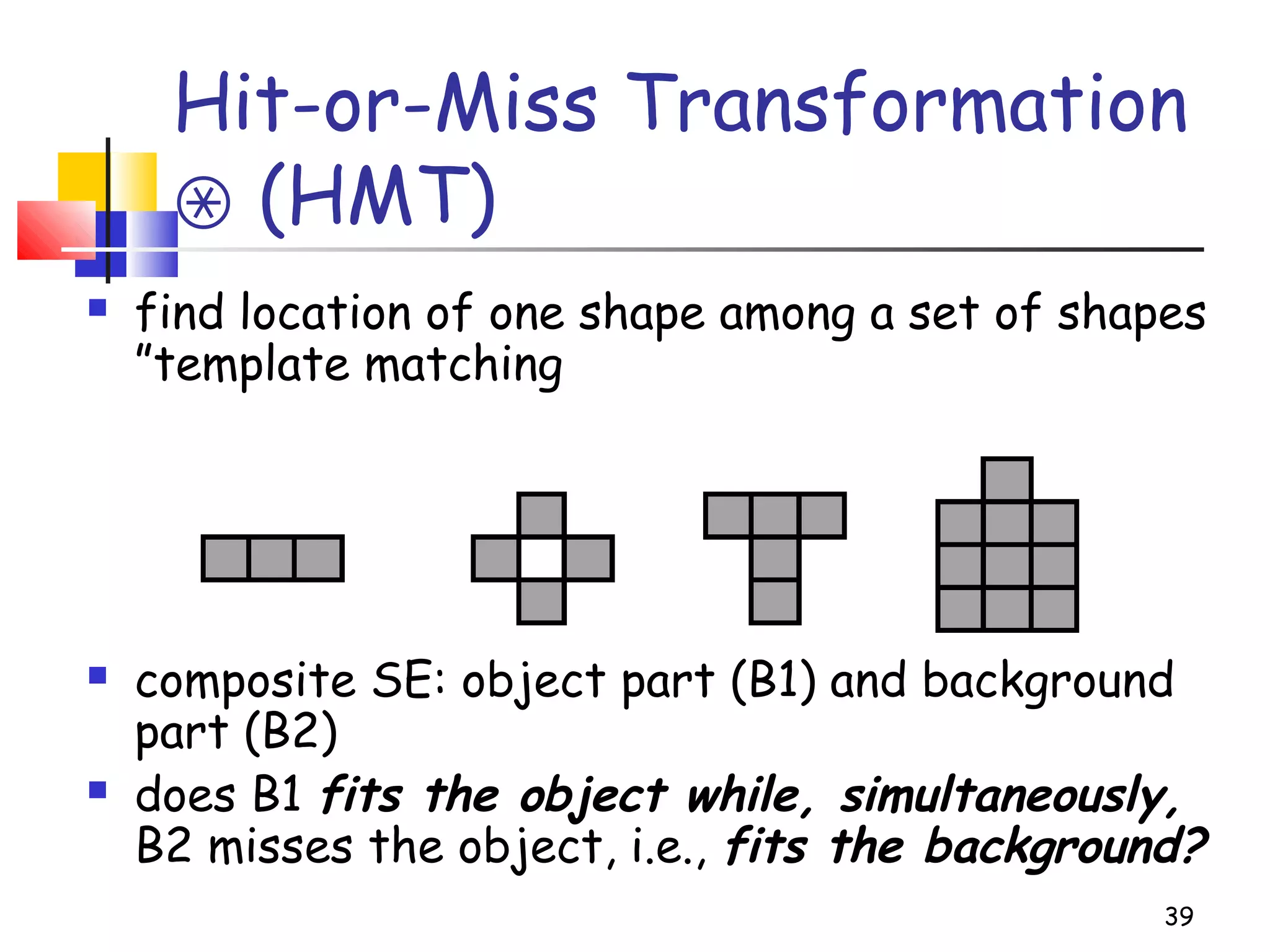
( XWAXABA c
−−∩−=∗](https://image.slidesharecdn.com/chapter9morphologicalimageprocessing-130613013223-phpapp02/75/morphological-image-processing-40-2048.jpg)