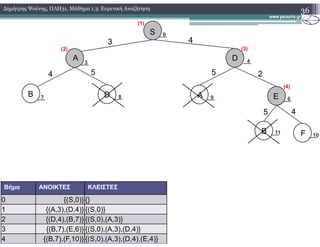
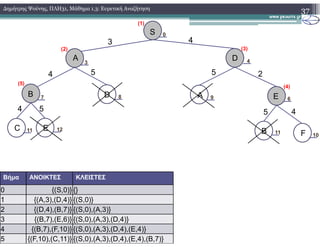
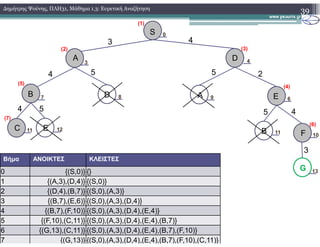
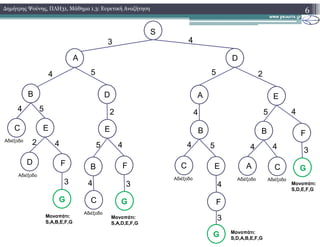
1) Συναρτήσεις Κόμβων 1.1) Συνάρτηση πραγματικού κόστους h* 1.2) Ευρετική Συνάρτηση h 1.3) Η συνάρτηση πραγματικού κόστους g 2) Αλγόριθμοι Ευρετικής Αναζήτησης 2.1) Ο αλγόριθμος Greedy 2.1.1) Ψευδογλώσσα 2.1.2) Παράδειγμα Εκτέλεσης 2.1.3) Παρατηρήσεις 2.1.4) Βελτιστότητα 2.1.5) Πληρότητα 2.1.6) Πολυπλοκότητα Χρόνου 2.1.7) Πολυπλοκότητα Χώρου 2.2) Ο αλγόριθμος UCS 2.2.1) Ψευδογλώσσα 2.2.2) Παράδειγμα Εκτέλεσης 2.2.3) Παρατηρήσεις 2.2.4) Βελτιστότητα 2.2.5) Πληρότητα 2.2.6) Πολυπλοκότητα Χρόνου 2.2.7) Πολυπλοκότητα Χώρου 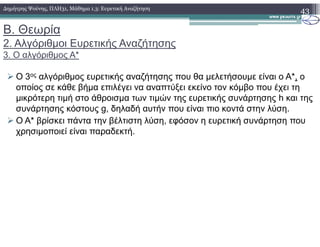2.3) Ο αλγόριθμος A* 2.3.1) Ψευδογλώσσα 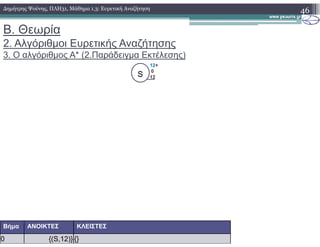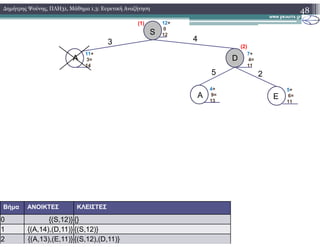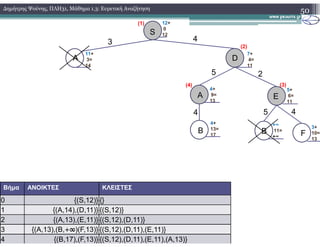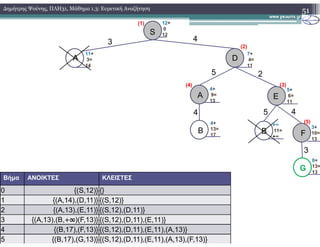2.3.2) Παράδειγμα Εκτέλεσης 2.3.3) Παρατηρήσεις 2.3.4) Βελτιστότητα 2.3.5) Πληρότητα 2.3.6) Πολυπλοκότητα Χρόνου 2.3.7) Πολυπλοκότητα Χώρου Ασκήσεις

1. ΠΛΗ31
ΕΝΟΤΗΤΑ 1: ΑΝΑΖΗΤΗΣΗ
Μάθηµα 1.3:
Ευρετική ΑναζήτησηΕυρετική Αναζήτηση
∆ηµήτρης Ψούνης

2. ΠΕΡΙΕΧΟΜΕΝΑ
2∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Α. Σκοπός του Μαθήµατος
Β.Θεωρία
1. Συναρτήσεις κόµβων
1. Η συνάρτηση πραγµατικού κόστους
h*(v)
2. H ευρετική συνάρτηση h(v)
3. Η συνάρτηση πραγµατικού κόστους
g(v)
2. Ο Αλγόριθµος UCS
1. Ψευδογλώσσα
2. Παράδειγµα Εκτέλεσης
3. Παρατηρήσεις
4. Βελτιστότητα
5. Πληρότητα
6. Πολυπλοκότητα Χρόνου
7. Πολυπλοκότητα Χώρου
3. Ο Αλγόριθµος A*g(v)
2. Αλγόριθµοι Ευρετικής
Αναζήτησης
1. Ο αλγόριθµος Greedy
1. Ψευδογλώσσα
2. Παράδειγµα Εκτέλεσης
3. Παρατηρήσεις
4. Βελτιστότητα
5. Πληρότητα
6. Πολυπλοκότητα Χρόνου
7. Πολυπλοκότητα Χώρου
3. Ο Αλγόριθµος A*
1. Ψευδογλώσσα
2. Παράδειγµα Εκτέλεσης
3. Παρατηρήσεις
4. Βελτιστότητα
5. Πληρότητα
6. Πολυπλοκότητα Χρόνου
7. Πολυπλοκότητα Χώρου
Γ.Ασκήσεις

3. Α. Σκοπός του Μαθήµατος
Επίπεδο Α
Συναρτήσεις Κόµβων
Ο άπληστος αλγόριθµος ευρετικής αναζήτησης
Ο αλγόριθµος UCS
Ο αλγόριθµος A*
Επίπεδο Β
3∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Επίπεδο Β
Ευρετικές Συναρτήσεις για συγκεκριµένα προβλήµατα
Επίπεδο Γ
(-)

4. Β. Θεωρία
1. Συναρτήσεις Κόµβων
Στα προηγούµενα:
Ορίσαµε τον χώρο καταστάσεων που περιέχει όλους τους
συνδυασµούς καταστάσεων-µεταβάσεων
Ορίσαµε τον χώρο αναζήτησης να περιέχει όλα τα µονοπάτια από την
αφετηρία προς τον κόµβο-στόχο
Ορίσαµε το δένδρο αναζήτησης ως το µέρος του χώρου αναζήτησης
4∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ορίσαµε το δένδρο αναζήτησης ως το µέρος του χώρου αναζήτησης
που παράγεται από εναν αλγόριθµο αναζήτησης
Μελετήσαµε τους αλγόριθµους τυφλής αναζήτησης κατά βάθος και
κατά πλάτος που παράγουν ένα µονοπάτι χωρίς να λαµβάνουν υπόψιν
τα κόστη των ακµών
Οι αλγόριθµοι ευρετικής αναζήτησης θα παράγουν ένα µονοπάτι
λαµβάνοντας υπόψιν τα κόστη των ακµών.
ΧΩΡΟΣ ΚΑΤΑΣΤΑΣΕΩΝ ΧΩΡΟΣ ΑΝΑΖΗΤΗΣΗΣ ∆ΕΝ∆ΡΟ ΑΝΑΖΗΤΗΣΗΣ ΤΗΣ ΚΑΤΑ ΒΑΘΟΣ

5. Β. Θεωρία
1. Συναρτήσεις Κόµβων
Το παράδειγµα ενός χώρου καταστάσεων στο οποίο θα εργαστούµε:
5∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
3
4 4
A B C
Αρχική κατάσταση είναι η S και τελική κατάσταση είναι η G. Στην επόµενη
διαφάνεια φαίνεται ο χώρος αναζήτησης
3
4
5
2
5
4
3
S
D E F
G

6. 6∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S
A
DB
D
A E
3 4
5 54
425 54 4
2
E
F
C
G
D
E
B F
C G
B
C E
F
G
B F
A C G
4
2 5 5
4
4 44 4
43
3
3
3
Μονοπάτι:
S,A,B,E,F,G
Μονοπάτι:
S,A,D,E,F,G
Μονοπάτι:
S,D,A,B,E,F,G
Μονοπάτι:
S,D,E,F,G
Αδιέξοδο
Αδιέξοδο
Αδιέξοδο
Αδιέξοδο Αδιέξοδο Αδιέξοδο

7. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
1. Συνάρτηση πραγµατικού κόστους h*(v)
Αν υπάρχουν περισσότερα από ένα µονοπάτια που οδηγούν από την v στον
κόµβο-στόχο, τότε η τιµή της συνάρτησης h*(v) είναι το κόστος του
7∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ορίζουµε την συνάρτηση πραγµατικού κόστους h*(v) του κόµβου v του χώρου
αναζήτησης ως το κόστος (σε άθροισµα βαρών ακµών) του βέλτιστου
µονοπατιού από την v προς τον κόµβο-στόχο.
κόµβο-στόχο, τότε η τιµή της συνάρτησης h*(v) είναι το κόστος του
καλύτερου από τα διαθέσιµα µονοπάτια.
Έπεται άµεσα:
Για την τελική κατάσταση Τ: h*(Τ)=0
Για µία κατάσταση v που δεν οδηγεί στην τελική κατάσταση: h*(v)=+∞
Στην επόµενη διαφάνεια έχει σηµειωθεί σε κάθε κόµβο η συνάρτηση
πραγµατικού κόστους από κάθε κατάσταση προς τον κόµβο στόχο.

8. 8∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S
A
DB
D
A E
3 4
5 54
425 54 4
2
12 9
14
16 7
9
13
Με κόκκινο χρώµα φαίνεται η
συναρτηση h* για κάθε κόµβο
E
F
C
G
D
E
B F
C G
B
C E
F
G
B F
A C G
4
2 5 5
4
4 44 4
43
3
3
3
Μονοπάτι:
S,A,B,E,F,G
Μονοπάτι:
S,A,D,E,F,G Μονοπάτι:
S,D,A,B,E,F,G
Μονοπάτι:
S,D,E,F,G
0
3+∞
+∞ 7
0+∞
+∞ 3
7
0
3
+∞ 7
12
+∞ +∞
+∞
0
3

9. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
1. Συνάρτηση πραγµατικού κόστους h*(v)
Αν γνωρίζαµε την συνάρτηση πραγµατικού κόστους, τότε θα µπορούσαµε
να αναπτύξουµε τους κόµβους µε βάση την κορυφή που έχει την µικρότερο
κόστος.
Συγκεκριµένα ο αλγόριθµος θα έτρεχε ως εξής:
9∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
∆ηλαδή θα µπορούσαµε «εύκολα» να υπολογίσουµε την βέλτιστη λύση.

10. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
2. Ευρετική Συνάρτηση h(v)
Στην πράξη δεν µπορούµε να γνωρίζουµε την συνάρτηση πραγµατικού
κόστους.
Για παράδειγµα στο σκάκι αν είχαµε τέτοια συνάρτηση θα µπορούσαµε να
ξέρουµε ποια είναι η «καλύτερη» κίνηση σε κάθε κατάσταση της παρτίδας.
10∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ορίζουµε την Ευρετική Συνάρτηση h(v) του κόµβου v του χώρου αναζήτησης
Η συνάρτηση h(v) «µαντεύει» το κόστος µετάβασης, εκτιµώντας πόσο
υποσχόµενη είναι η κατάσταση v για να µας οδηγήσει στον κόµβο-
στόχο.
Η κατασκευή της γίνεται ενσωµατώνοντας ευρετικούς κανόνες που
εξαρτώνται από το πρόβληµα.
Ορίζουµε την Ευρετική Συνάρτηση h(v) του κόµβου v του χώρου αναζήτησης
ως µία εκτίµηση του πόσο απέχει ο κόµβος από έναν κόµβο-στόχο.
Μια ευρετική συνάρτηση λέγεται παραδεκτή αν δεν υπερεκτιµά το
πραγµατικό κόστος του κόµβου, δηλαδή: h(v)≤h*(v) για κάθε κόµβο v του
χώρου αναζήτησης.

11. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
2. Ευρετική Συνάρτηση h(v)
Η ευρετική συνάρτηση *εκτιµάει* ποια είναι η απόσταση του τρέχοντος
κόµβου από τον κόµβο στόχο.
11∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
s
Επιθυµούµε να έχουµε εκτιµήσεις που δεν υπερβαίνουν το βέλτιστο κόστος,
διότι τότε θα δουλεύουν αποδοτικά οι αλγόριθµοί µας.
Ας δούµε δύο παραδείγµατα παραδεκτών ευρετικών συναρτήσεων.
v
t
h(v) και επιθυµώ h(v)≤h*(v)

12. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
2. Ευρετική Συνάρτηση h(v): Προβλήµατα Χαρτών
Σε προβλήµατα εύρεσης µονοπατιού σε ένα χάρτη,µπορούµε να ορίσουµε
ως ευρετική συνάρτηση την απόσταση ευθειας γραµµής.
12∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Βέλτιστη ∆ιαδροµή
Απόσταση Ευθείας
Η απόσταση ευθείας γραµµης δεν υπερεκτιµά ποτέ τη βέλτιστη απόσταση,
άρα πρόκειται για µια παραδεκτή ευρετική συνάρτηση.
Απόσταση Ευθείας
Γραµµής

13. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
2. Ευρετική Συνάρτηση h(v): Προβλήµατα Λαβυρίνθων
Σε προβλήµατα λαβυρίνθων ορίζεται η απόσταση Manhattan του κόµβου
από τον κόµβο-στόχο σύµφωνα µε τον τύπο:
13∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Υ
1 2 3 4
manhattan ((x1,y1),(x2,y2)) = |x1-x2|+|y1-y2|
Υ
1 2 3 4
Κόµβος
Η απόσταση Manhattan υπολογίζει το πλήθος µετακινήσεων σαν µην
υπάρχουν εµπόδια, άρα δεν υπερεκτιµά ποτέ το πραγµατικό κόστος.
1 2 3 4
Χ
1 4 3 2 3
2 3 2
3 2 Τ Τ 1
4 3 2 1 2
1 2 3 4
Χ
1
2
3 Τ Τ
4
Κόµβος
Στόχος
Είναι το
τετράγωνο
(3,3)

14. Β. Θεωρία
1. Συναρτήσεις Κόµβων ∆ένδρου
3. Συνάρτηση κόστους διαδροµής g(v)
H συνάρτηση αυτή υπολογίζει το κόστος που ήδη έχουµε πληρώσει για
να φτάσουµε µέχρι τον κόµβο v.
Χρησιµοποιείται από τους αλγόριθµους Α* και UCS για τον υπολογισµό
14∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
H Συνάρτηση Κόστους διαδροµής g(v) του κόµβου v του χώρου αναζήτησης
είναι το άθροισµα των βαρών των ακµών από την ρίζα µέχρι και τον κόµβο v.
Χρησιµοποιείται από τους αλγόριθµους Α* και UCS για τον υπολογισµό
του επόµενου κόµβου που θα αναπτυχθεί.
v
t
s
h(v) και επιθυµώ h(v)≤h*(v)
g(v) πόσο έχω πληρώσει µέχρι τον v

15. 15∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S
A
DB
D
A E
3 4
5 54
425 54 4
2
12 9
14
16 7
9
13
Με κόκκινο χρώµα φαίνεται η
συναρτηση h* για κάθε κόµβο
Με µπλε χρώµα φαίνεται η
συναρτηση h για κάθε κόµβο
12/0
11/3 7/4
7/7 7/8 4/9 5/6
Με καφέ χρώµα φαίνεται η
συναρτηση g για κάθε κόµβο
E
F
C
G
D
E
B F
C G
B
C E
F
G
B F
A C G
4
2 5 5
4
4 44 4
43
3
3
3
Μονοπάτι:
S,A,B,E,F,G
Μονοπάτι:
S,A,D,E,F,G Μονοπάτι:
S,D,A,B,E,F,G
Μονοπάτι:
S,D,E,F,G
0
3+∞
+∞ 7
0+∞
+∞ 3
7
0
3
+∞ 7
12
+∞ +∞
+∞
0
3
+∞/11
4/12
+∞/14 +∞/15
2/16
5/10
2/14
4/13
+∞/17 6/18
+∞/11
+∞/15 +∞/15
0/17 3/22
0/19
0/25
0/13
3/10
+∞/19

16. Β. Θεωρία
3. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Ο απληστος αλγόριθµος
Οι αλγόριθµοι Ευρετικής Αναζήτησης λαµβάνουν υπόψιν τα βάρη των
ακµών µε στόχο να βρουν ένα µονοπάτι από την αρχική κατάσταση στην
τελική.
Ο 1ος αλγόριθµος ευρετικής αναζήτησης που θα µελετήσουµε είναι ο
άπληστος αλγόριθµος ο οποίος σε κάθε βήµα επιλέγει να αναπτύξει εκείνο
16∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
άπληστος αλγόριθµος ο οποίος σε κάθε βήµα επιλέγει να αναπτύξει εκείνο
τον κόµβο που έχει το µικρότερο ευρετικό κόστος, δηλαδή αυτήν που
*φαίνεται* ότι θα οδηγήσει πιο γρήγορα στην βέλτιστη λύση.

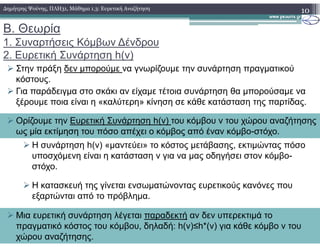
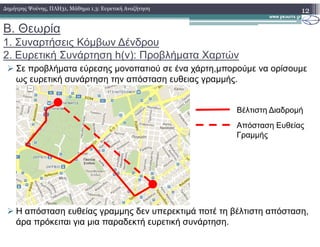
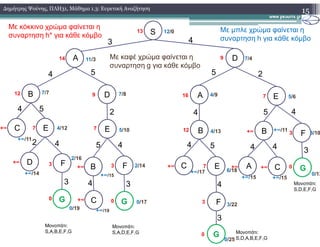
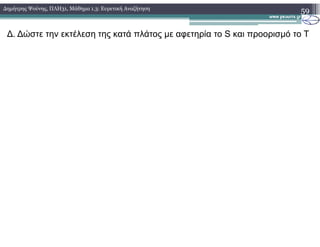
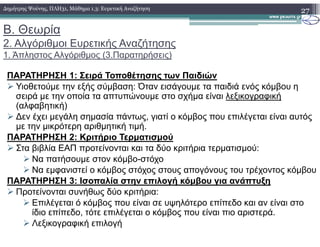
17. Β. Θεωρία
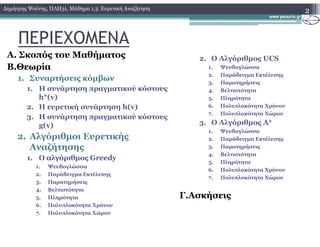
3. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Ο άπληστος αλγόριθµος (1.Ψευδογλώσσα)
17∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
GREEDY(S,T)
ΑΝΟΙΚΤΕΣ=[(S,f(S))]
ΚΛΕΙΣΤΕΣ=[]
Επανέλαβε:
1.Αφαίρεσε την κατάσταση v της λίστας ΑΝΟΙΚΤΕΣ µε την ιδιότητα
f(v)≤f(u) για κάθε άλλη κατάσταση u της λίστας ΑΝΟΙΚΤΕΣ
2.Βάλε το v στην λίστα ΚΛΕΙΣΤΕΣ
3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v
είναι προκάτοχός της.
4.Εάν το v είναι ο κόµβος στόχος τερµάτισε µε επιστροφή
µονοπατιού
Αλλιώς επανέλαβε τα ακόλουθα για κάθε διάδοχο u της κατάστασης v:
4.1 Υπολόγισε την τιµή f(u)
4.2 Εάν (η u δεν ανήκει ούτε στις ΑΝΟΙΚΤΕΣ, ούτε στις ΚΛΕΙΣΤΕΣ) τότε
Πρόσθεσε την τιµή (u,f(u)) στις ανοικτές
Αλλιώς εάν (η u ήδη ανήκει στις ΑΝΟΙΚΤΕΣ ή ΚΛΕΙΣΤΕΣ) τότε
Συγκρίνουµε την νέα τιµή της f(u) µε την παλαιά τιµή της)
Εάν (νεα>=παλαιά) τότε αφαιρούµε την u από τους διαδόχους της v
Αλλιώς Αφαιρούµε το (u,παλαία) από την λίστα που ανήκει
Προσθέτουµε το (u,νέα) στην λίστα ΑΝΟΙΚΤΕΣ
Εως ότου η λίστα ΑΝΟΙΚΤΕΣ είναι κενή.
Στον ψευδοκωδικα νοείται ως f(x) η συνάρτηση h(x)

18. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Ο άπληστος αλγόριθµος(1.Ψευδογλώσσα)
Εµπειρικά:
18∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
ΑΠΛΗΣΤΟΣ ΑΛΓΟΡΙΘΜΟΣ
Αρχικά:
• Βάζουµε την αφετηρία στο δένδρο µε τιµή f(x)=h(x).
Επαναληπτικά:Επαναληπτικά:
• Πατάµε στον ανοιχτό κόµβο µε την µικρότερη τιµή.
• Ανοίγουµε τους γείτονες του (που δεν είναι πρόγονοί του) στον γράφο και τους
θέτουµε ως παιδιά του µε τιµή f(v)=h(v).
• Απο κάθε παιδί κρατάµε την καλύτερη εµφάνιση του στο δένδρο:
• Αν δεν προϋπήρχε στο δένδρο τότε το αφήνουµε ανοιχτό.
• Αν προυπήρχε στο δένδρο µε µικρότερη ή ίση τιµή, τότε το διαγράφουµε.
• Αν προϋπήρχε στο δένδρο µε µεγαλύτερη τιµή, το κρατάµε και διαγράφουµε την
προϋπάρχουσα τιµή.
Εως ότου:
• Πατήσουµε στον κόµβο-στόχο

19. 12
19∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S
Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Ο άπληστος αλγόριθµος(2.Παράδειγµα Εκτέλεσης)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}

20. 20∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A D
12S
(1)
11 7
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}

21. 21∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}

22. 22∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
(3)
B 4
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}
3 {(B,4),(E,5)} {(S,12),(D,7),(A,4)}

23. 23∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
(3)
(4)
C E
B 4
+∞ 6
(4)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}
3 {(B,4),(E,5)} {(S,12),(D,7),(A,4)}
4 {(C,+∞),(E,5)} {(S,12),(D,7),(A,4),(B,4)}

24. 24∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
(3)
(4)
(5)
B F
C E
B 4
+∞ 6
(4)
+∞
3
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}
3 {(B,4),(E,5)} {(S,12),(D,7),(A,4)}
4 {(C,+∞),(E,5)} {(S,12),(D,7),(A,4),(B,4)}
5 {(C,+∞),(F,3)} {(S,12),(D,7),(A,4),(B,4),
(E,5)}

25. 25∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
(3)
(4)
(5)
(6)
G0
0
B F
C E
B 4
+∞ 6
(4)
+∞
3
(6)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}
3 {(B,4),(E,5)} {(S,12),(D,7),(A,4)}
4 {(C,+∞),(E,5)} {(S,12),(D,7),(A,4),(B,4)}
5 {(C,+∞),(F,3)} {(S,12),(D,7),(A,4),(B,4),
(E,5)}
6 {(C,+∞),(G,0)} {(S,12),(D,7),(A,4),(B,4),
(E,5),(F,3)}

26. 26∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
A D
12S
(1)
11 7
(2)
4 5
(3)
(4)
(5)
(6)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(Α,11),(D,7)} {(S,12)}
2 {(Α,4),(E,5)} {(S,12),(D,7)}
G
B F
C E
B 4
+∞ 6
(4)
+∞
3
(6)
0
(7)
3 {(B,4),(E,5)} {(S,12),(D,7),(A,4)}
4 {(C,+∞),(E,5)} {(S,12),(D,7),(A,4),(B,4)}
5 {(C,+∞),(F,3)} {(S,12),(D,7),(A,4),(B,4),
(E,5)}
6 {(C,+∞),(G,0)} {(S,12),(D,7),(A,4),(B,4),
(E,5),(F,3)}
7 {(C,+∞)} {(S,12),(D,7),(A,4),(B,4),
(E,5),(F,3),(G,0)}
Μονοπάτι: S-D-E-F-G
Κόστος Μονοπατιού: 13
Σειρά Επίσκεψης: S-D-A-E-B-F-G
Βήµατα: 7

27. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Άπληστος Αλγόριθµος (3.Παρατηρήσεις)
ΠΑΡΑΤΗΡΗΣΗ 1: Σειρά Τοποθέτησης των Παιδιών
Υιοθετούµε την εξής σύµβαση: Όταν εισάγουµε τα παιδιά ενός κόµβου η
σειρά µε την οποία τα απτυπώνουµε στο σχήµα είναι λεξικογραφική
(αλφαβητική)
∆εν έχει µεγάλη σηµασία πάντως, γιατί ο κόµβος που επιλέγεται είναι αυτός
µε την µικρότερη αριθµητική τιµή.
27∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
µε την µικρότερη αριθµητική τιµή.
ΠΑΡΑΤΗΡΗΣΗ 2: Κριτήριο Τερµατισµού
Στα βιβλία ΕΑΠ προτείνονται και τα δύο κριτήρια τερµατισµού:
Να πατήσουµε στον κόµβο-στόχο
Να εµφανιστεί ο κόµβος στόχος στους απογόνους του τρέχοντος κόµβου
ΠΑΡΑΤΗΡΗΣΗ 3: Ισοπαλία στην επιλογή κόµβου για ανάπτυξη
Προτείνονται συνήθως δύο κριτήρια:
Επιλέγεται ό κόµβος που είναι σε υψηλότερο επίπεδο και αν είναι στο
ίδιο επίπεδο, τότε επιλέγεται ο κόµβος που είναι πιο αριστερά.
Λεξικογραφική επιλογή

28. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
1. Άπληστος Αλγόριθµος (4.Χαρακτηριστικά)
Τα χαρακτηριστικά του άπληστου αλγορίθµου είναι τα ακόλουθα:
ΠΛΗΡΟΤΗΤΑ
Ναι, εγγυάται την εύρεση µονοπατιού εφόσον αυτό υπάρχει.
ΒΕΛΤΙΣΤΟΤΗΤΑ
Οχι. ∆εν βρίσκει την βέλτιστη λύση
28∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Οχι. ∆εν βρίσκει την βέλτιστη λύση
ΧΡΟΝΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)
ΧΩΡΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)

29. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Ο αλγόριθµος UCS
Ο 2ος αλγόριθµος ευρετικής αναζήτησης που θα µελετήσουµε είναι ο UCS
(Uniform Cost Search) ο οποίος σε κάθε βήµα επιλέγει να αναπτύξει εκείνο
τον κόµβο που έχει το µικρότερο κόστος διαδροµής, δηλαδή αυτήν που είναι
πιο κοντά στην ρίζα.
Η UCS βρίσκει πάντα την βέλτιστη λύση γιατι στην ουσία κατασκευάζει
29∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Η UCS βρίσκει πάντα την βέλτιστη λύση γιατι στην ουσία κατασκευάζει
διαδοχικά όλα τα µονοπάτια από την αφετηρία µε αύξουσα σειρά κόστους
(λειτουργεί όπως ο αλγόριθµος του Dijkstra)

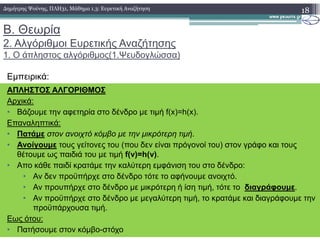
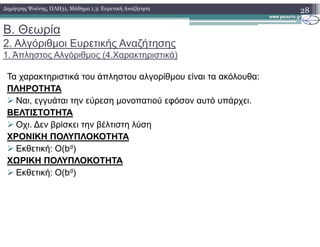
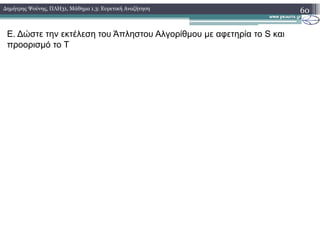
30. Β. Θεωρία
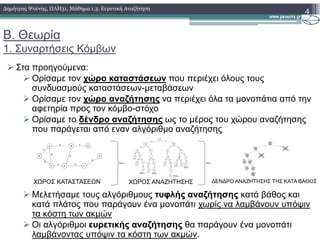
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Ο αλγόριθµος UCS (1.Ψευδογλώσσα)
30∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
UCS(S,T)
ΑΝΟΙΚΤΕΣ=[(S,f(S))]
ΚΛΕΙΣΤΕΣ=[]
Επανέλαβε:
1.Αφαίρεσε την κατάσταση v της λίστας ΑΝΟΙΚΤΕΣ µε την ιδιότητα
f(v)≤f(u) για κάθε άλλη κατάσταση u της λίστας ΑΝΟΙΚΤΕΣ
2.Βάλε το v στην λίστα ΚΛΕΙΣΤΕΣ
3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v
είναι προκάτοχός της.
4.Εάν το v είναι ο κόµβος στόχος τερµάτισε µε επιστροφή
µονοπατιού
Αλλιώς επανέλαβε τα ακόλουθα για κάθε διάδοχο u της κατάστασης v:
4.1 Υπολόγισε την τιµή f(u)
4.2 Εάν (η u δεν ανήκει ούτε στις ΑΝΟΙΚΤΕΣ, ούτε στις ΚΛΕΙΣΤΕΣ) τότε
Πρόσθεσε την τιµή (u,f(u)) στις ανοικτές
Αλλιώς εάν (η u ήδη ανήκει στις ΑΝΟΙΚΤΕΣ ή ΚΛΕΙΣΤΕΣ) τότε
Συγκρίνουµε την νέα τιµή της f(u) µε την παλαιά τιµή της)
Εάν (νεα>=παλαιά) τότε αφαιρούµε την u από τους διαδόχους της v
Αλλιώς Αφαιρούµε το (u,παλαία) από την λίστα που ανήκει
Προσθέτουµε το (u,νέα) στην λίστα ΑΝΟΙΚΤΕΣ
Εως ότου η λίστα ΑΝΟΙΚΤΕΣ είναι κενή.
Στον ψευδοκωδικα νοείται ως f(x) η συνάρτηση g(x)

31. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Ο αλγόριθµος UCS (1.Ψευδογλώσσα)
Εµπειρικά:
31∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
ΑΛΓΟΡΙΘΜΟΣ UCS
Αρχικά:
• Βάζουµε την αφετηρία στο δένδρο µε τιµή f(x)=g(x).
Επαναληπτικά:Επαναληπτικά:
• Πατάµε στον ανοιχτό κόµβο µε την µικρότερη τιµή.
• Ανοίγουµε τους γείτονες του (που δεν είναι πρόγονοί του) στον γράφο και τους
θέτουµε ως παιδιά του µε τιµή f(v)=g(v).
• Απο κάθε παιδί κρατάµε την καλύτερη εµφάνιση του στο δένδρο:
• Αν δεν προϋπήρχε στο δένδρο τότε το αφήνουµε ανοιχτό.
• Αν προυπήρχε στο δένδρο µε µικρότερη ή ίση τιµή, τότε το διαγράφουµε.
• Αν προϋπήρχε στο δένδρο µε µεγαλύτερη τιµή, το κρατάµε και διαγράφουµε την
προϋπάρχουσα τιµή.
Εως ότου:
• Πατήσουµε στον κόµβο-στόχο

32. 32
S 0
∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Ο αλγόριθµος UCS (2.Παράδειγµα Εκτέλεσης)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}

33. 33∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A D
3 4
S 0
(1)
3 4
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}

34. 34∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}

35. 35∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}

36. 36∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
5 4
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
(4)
B F11
10
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}
4 {(B,7),(F,10)} {(S,0),(A,3),(D,4),(E,4)}

37. 37∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
54 5 4
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
(4)
(5)
EC B F11
10
11 12
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}
4 {(B,7),(F,10)} {(S,0),(A,3),(D,4),(E,4)}
5 {(F,10),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7)}

38. 38∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
54 5 4
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
(4)
(5)
(6)
G
3
EC B F1111 12
10
13
(6)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}
4 {(B,7),(F,10)} {(S,0),(A,3),(D,4),(E,4)}
5 {(F,10),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7)}
6 {(G,13),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7),
(F,10)}
F

39. 39∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
54 5 4
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
(4)
(5)
(6)
(7)
G
3
EC B F1111 12
10
13
(6)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}
4 {(B,7),(F,10)} {(S,0),(A,3),(D,4),(E,4)}
5 {(F,10),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7)}
6 {(G,13),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7),(F,10)}
7 {(G,13)} {(S,0),(A,3),(D,4),(E,4),(B,7),(F,10),(C,11)}

40. 40∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
54 5 4
A E
5 2
DB
54
A D
3 4
S 0
(1)
3 4
(2)
7 8
(3)
9 6
(4)
(5)
(6)
(7)
G
3
EC B F1111 12
10
13
(6)
(8)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,0)} {}
1 {(A,3),(D,4)} {(S,0)}
2 {(D,4),(B,7)} {(S,0),(A,3)}
3 {(B,7),(E,6)} {(S,0),(A,3),(D,4)}
4 {(B,7),(F,10)} {(S,0),(A,3),(D,4),(E,4)}
5 {(F,10),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7)}
6 {(G,13),(C,11)} {(S,0),(A,3),(D,4),(E,4),(B,7),(F,10)}
7 {(G,13)} {(S,0),(A,3),(D,4),(E,4),(B,7),(F,10),(C,11)}
8 {} {(S,0),(A,3),(D,4),(E,4),(B,7),(F,10),(C,11),(G,13)}
Μονοπάτι: S-D-E-F-G
Κόστος Μονοπατιού: 13
Σειρά Επίσκεψης:
S-A-D-E-B-F-C-G
Βήµατα: 8

41. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Αλγόριθµος UCS (3.Παρατηρήσεις)
ΠΑΡΑΤΗΡΗΣΗ 1: Σειρά Τοποθέτησης των Παιδιών
Υιοθετούµε την εξής σύµβαση: Όταν εισάγουµε τα παιδιά ενός κόµβου η
σειρά µε την οποία τα απτυπώνουµε στο σχήµα είναι λεξικογραφική
(αλφαβητική)
∆εν έχει µεγάλη σηµασία πάντως, γιατί ο κόµβος που επιλέγεται είναι αυτός
µε την µικρότερη αριθµητική τιµή.
41∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
µε την µικρότερη αριθµητική τιµή.
ΠΑΡΑΤΗΡΗΣΗ 2: Κριτήριο Τερµατισµού
Στα βιβλία ΕΑΠ προτείνονται και τα δύο κριτήρια τερµατισµού
Να πατήσουµε στον κόµβο-στόχο
Να εµφανιστεί ο κόµβος στόχος στους απογόνους του τρέχοντος κόµβου
ΠΑΡΑΤΗΡΗΣΗ 3: Ισοπαλία στην επιλογή κόµβου για ανάπτυξη
Προτείνονται συνήθως δύο κριτήρια:
Επιλέγεται ό κόµβος που είναι σε υψηλότερο επίπεδο και αν είναι στο
ίδιο επίπεδο, τότε επιλέγεται ο κόµβος που είναι πιο αριστερά.
Λεξικογραφική επιλογή

42. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Αλγόριθµος UCS (4.Χαρακτηριστικά)
Τα χαρακτηριστικά του άπληστου αλγορίθµου είναι τα ακόλουθα:
ΠΛΗΡΟΤΗΤΑ
Ναι, εγγυάται την εύρεση µονοπατιού εφόσον αυτό υπάρχει.
ΒΕΛΤΙΣΤΟΤΗΤΑ
Ναι. Εγγυάται την εύρεση της βέλτιστης λύσης
42∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ναι. Εγγυάται την εύρεση της βέλτιστης λύσης
ΧΡΟΝΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)
ΧΩΡΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)

43. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
3. Ο αλγόριθµος A*
Ο 3ος αλγόριθµος ευρετικής αναζήτησης που θα µελετήσουµε είναι ο A*, ο
οποίος σε κάθε βήµα επιλέγει να αναπτύξει εκείνο τον κόµβο που έχει τη
µικρότερη τιµή στο άθροισµα των τιµών της ευρετικής συνάρτησης h και της
συνάρτησης κόστους g, δηλαδή αυτήν που είναι πιο κοντά στην λύση.
O A* βρίσκει πάντα την βέλτιστη λύση, εφόσον η ευρετική συνάρτηση που
43∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
O A* βρίσκει πάντα την βέλτιστη λύση, εφόσον η ευρετική συνάρτηση που
χρησιµοποιεί είναι παραδεκτή.

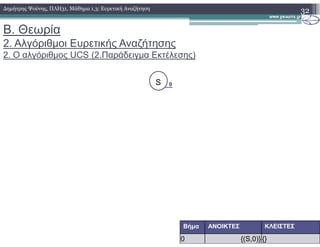
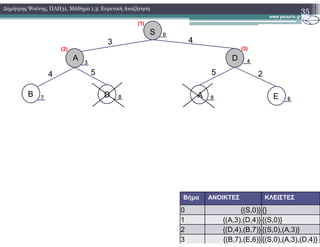
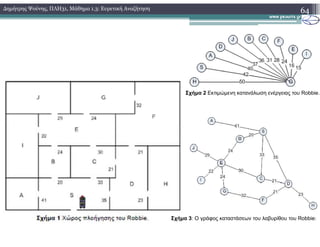
44. Β. Θεωρία
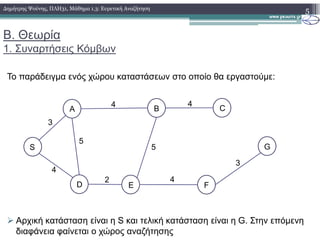
2. Αλγόριθµοι Ευρετικής Αναζήτησης
3. Ο αλγόριθµος Α* (1.Ψευδογλώσσα)
44∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Α*(S,T)
ΑΝΟΙΚΤΕΣ=[(S,f(S))]
ΚΛΕΙΣΤΕΣ=[]
Επανέλαβε:
1.Αφαίρεσε την κατάσταση v της λίστας ΑΝΟΙΚΤΕΣ µε την ιδιότητα
f(v)≤f(u) για κάθε άλλη κατάσταση u της λίστας ΑΝΟΙΚΤΕΣ
2.Βάλε το v στην λίστα ΚΛΕΙΣΤΕΣ
3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v3.∆ηµιουργησε τους διαδόχους της v. Κάθε διάδοχος κρατάει ότι η v
είναι προκάτοχός της.
4.Εάν το v είναι ο κόµβος στόχος τερµάτισε µε επιστροφή
µονοπατιού
Αλλιώς επανέλαβε τα ακόλουθα για κάθε διάδοχο u της κατάστασης v:
4.1 Υπολόγισε την τιµή f(u)
4.2 Εάν (η u δεν ανήκει ούτε στις ΑΝΟΙΚΤΕΣ, ούτε στις ΚΛΕΙΣΤΕΣ) τότε
Πρόσθεσε την τιµή (u,f(u)) στις ανοικτές
Αλλιώς εάν (η u ήδη ανήκει στις ΑΝΟΙΚΤΕΣ ή ΚΛΕΙΣΤΕΣ) τότε
Συγκρίνουµε την νέα τιµή της f(u) µε την παλαιά τιµή της)
Εάν (νεα>=παλαιά) τότε αφαιρούµε την u από τους διαδόχους της v
Αλλιώς Αφαιρούµε το (u,παλαία) από την λίστα που ανήκει
Προσθέτουµε το (u,νέα) στην λίστα ΑΝΟΙΚΤΕΣ
Εως ότου η λίστα ΑΝΟΙΚΤΕΣ είναι κενή.
Στον ψευδοκωδικα νοείται ως f(x) η συνάρτηση g(x)+h(x)

45. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
2. Ο αλγόριθµος A* (1.Ψευδογλώσσα)
Εµπειρικά:
45∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
ΑΛΓΟΡΙΘΜΟΣ A*
Αρχικά:
• Βάζουµε την αφετηρία στο δένδρο µε τιµή f(x)=g(x)+h(x).
Επαναληπτικά:Επαναληπτικά:
• Πατάµε στον ανοιχτό κόµβο µε την µικρότερη τιµή.
• Ανοίγουµε τους γείτονες του (που δεν είναι πρόγονοί του) στον γράφο και τους
θέτουµε ως παιδιά του µε τιµή f(v)=g(v)+h(v).
• Απο κάθε παιδί κρατάµε την καλύτερη εµφάνιση του στο δένδρο:
• Αν δεν προϋπήρχε στο δένδρο τότε το αφήνουµε ανοιχτό.
• Αν προυπήρχε στο δένδρο µε µικρότερη ή ίση τιµή, τότε το διαγράφουµε.
• Αν προϋπήρχε στο δένδρο µε µεγαλύτερη τιµή, το κρατάµε και διαγράφουµε την
προϋπάρχουσα τιµή.
Εως ότου:
• Πατήσουµε στον κόµβο-στόχο

46. 46
12+
0
12
∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S
Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
3. Ο αλγόριθµος A* (2.Παράδειγµα Εκτέλεσης)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}

47. 47∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}

48. 48∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
A E
5 2
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
(2)
4+
9=
13
5+
6=
11
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}
2 {(A,13),(E,11)} {(S,12),(D,11)}

49. 49∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
5 4
A E
5 2
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
(2)
4+
9=
13
5+
6=
11
(3)
+∞
B F
+∞
11=
+∞
3+
10=
13
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}
2 {(A,13),(E,11)} {(S,12),(D,11)}
3 {(A,13),(B,+∞)(F,13)} {(S,12),(D,11),(E,11)}

50. 50∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
4 5 4
A E
5 2
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
(2)
4+
9=
13
5+
6=
11
(3)
+∞
(4)
4+
B B F
+∞
11=
+∞
4+
13=
17
3+
10=
13
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}
2 {(A,13),(E,11)} {(S,12),(D,11)}
3 {(A,13),(B,+∞)(F,13)} {(S,12),(D,11),(E,11)}
4 {(B,17),(F,13)} {(S,12),(D,11),(E,11),(A,13)}

51. 51∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
4 5 4
A E
5 2
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
(2)
4+
9=
13
5+
6=
11
(3)
+∞
(4)
4+ (5)
G
3
B B F
+∞
11=
+∞
4+
13=
17
3+
10=
13
0+
13=
13
(5)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}
2 {(A,13),(E,11)} {(S,12),(D,11)}
3 {(A,13),(B,+∞)(F,13)} {(S,12),(D,11),(E,11)}
4 {(B,17),(F,13)} {(S,12),(D,11),(E,11),(A,13)}
5 {(B,17),(G,13)} {(S,12),(D,11),(E,11),(A,13),(F,13)}

52. 52∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
4 5 4
A E
5 2
A D
3 4
12+
0
12S
(1)
11+
3=
14
7+
4=
11
(2)
4+
9=
13
5+
6=
11
(3)
+∞
(4)
4+ (5)
G
3
B B F
+∞
11=
+∞
4+
13=
17
3+
10=
13
0+
13=
13
(5)
(6)
Βήµα ΑΝΟΙΚΤΕΣ ΚΛΕΙΣΤΕΣ
0 {(S,12)} {}
1 {(A,14),(D,11)} {(S,12)}
2 {(A,13),(E,11)} {(S,12),(D,11)}
3 {(A,13),(B,+∞)(F,13)} {(S,12),(D,11),(E,11)}
4 {(B,17),(F,13)} {(S,12),(D,11),(E,11),(A,13)}
5 {(B,17),(G,13)} {(S,12),(D,11),(E,11),(A,13),(F,13)}
6 {(B,17)} {(S,12),(D,11),(E,11),(A,13),(F,13),(G,13)}
Μονοπάτι: S-D-E-F-G
Κόστος Μονοπατιού: 13
Σειρά Επίσκεψης:
S-D-A-E-F-G
Βήµατα: 6

53. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
3. Αλγόριθµος A*(3.Παρατηρήσεις)
ΠΑΡΑΤΗΡΗΣΗ 1: Σειρά Τοποθέτησης των Παιδιών
Υιοθετούµε την εξής σύµβαση: Όταν εισάγουµε τα παιδιά ενός κόµβου η
σειρά µε την οποία τα απτυπώνουµε στο σχήµα είναι λεξικογραφική
(αλφαβητική)
∆εν έχει µεγάλη σηµασία πάντως, γιατί ο κόµβος που επιλέγεται είναι αυτός
53∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
∆εν έχει µεγάλη σηµασία πάντως, γιατί ο κόµβος που επιλέγεται είναι αυτός
µε την µικρότερη αριθµητική τιµή.
ΠΑΡΑΤΗΡΗΣΗ 2: Κριτήριο Τερµατισµού
Έχει διαλευκανθεί ότι το κριτήριο του τερµατισµού είναι πάντα:
Να πατήσουµε στον κόµβο-στόχο!
ΠΑΡΑΤΗΡΗΣΗ 3: Ισοπαλία στην επιλογή κόµβου για ανάπτυξη
Προτείνονται συνήθως δύο κριτήρια:
Επιλέγεται ό κόµβος που είναι σε υψηλότερο επίπεδο και αν είναι στο
ίδιο επίπεδο, τότε επιλέγεται ο κόµβος που είναι πιο αριστερά.
Λεξικογραφική επιλογή

54. Β. Θεωρία
2. Αλγόριθµοι Ευρετικής Αναζήτησης
3. Αλγόριθµος Α* (4.Χαρακτηριστικά)
Τα χαρακτηριστικά του άπληστου αλγορίθµου είναι τα ακόλουθα:
ΠΛΗΡΟΤΗΤΑ
Ναι, εγγυάται την εύρεση µονοπατιού εφόσον αυτό υπάρχει.
ΒΕΛΤΙΣΤΟΤΗΤΑ
Ναι αν η ευρετική συνάρτηση είναι παραδεκτή.
54∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ναι αν η ευρετική συνάρτηση είναι παραδεκτή.
ΧΡΟΝΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)
ΧΩΡΙΚΗ ΠΟΛΥΠΛΟΚΟΤΗΤΑ
Εκθετική: Ο(bd)

55. Γ. Ασκήσεις
Άσκηση Κατανόησης 1
∆ίδεται ο ακόλουθος γράφος καταστασεων µε κόµβο αφετηρία τον κόµβο S και
κόµβο-στόχο T:
55∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
4
A
και η ακόλουθη ευρετική συνάρτηση: h(S)=3, h(A)=2, h(B)=1, h(E)=2
1
2
1
3
2
S
Β
Τ
E

56. Α. Εξετάστε αν η ευρετική συνάρτηση είναι παραδεκτή.
56∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

57. Β. Κατασκευάστε τον χώρο αναζήτησης
57∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

58. Γ. ∆ώστε την εκτέλεση της κατά βάθος µε αφετηρία το S και προορισµό το Τ
58∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

59. ∆. ∆ώστε την εκτέλεση της κατά πλάτος µε αφετηρία το S και προορισµό το Τ
59∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

60. Ε. ∆ώστε την εκτέλεση του Άπληστου Αλγορίθµου µε αφετηρία το S και
προορισµό το Τ
60∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

61. Ζ. ∆ώστε την εκτέλεση της UCS µε αφετηρία το S και προορισµό το Τ
61∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

62. Η. ∆ώστε την εκτέλεση του Α* µε αφετηρία το S και προορισµό το Τ
62∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση

63. Γ. Ασκήσεις
Εφαρµογή 1
Το ροµπότ Robbie για να αποφασίσει ποια διαδροµή θα ακολουθήσει κατά την
πλοήγηση του στο χώρο που παρουσίαζεται στο σχήµα λαµβάνει υπόψη την
κατανάλωση ενέργειας της µπαταρίας του. Στο σχήµα 1 φαίνεται ο χώρος
πλοήγησης του Robbie. Κάθε δωµάτιο χαρακτηρίζεται από το όνοµά του και
περιέχει θέσεις πρόσβασης σε γειτονικό του τετράγωνο. Κάθε θέση
πρόσβασης χαρακτηρίζεται από έναν αριθµό που περιγράφει το ποσό
63∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
πρόσβασης χαρακτηρίζεται από έναν αριθµό που περιγράφει το ποσό
ενέργειας πραγµατικής κατανάλωσης της µπαταρίας του Robbie.
Ο γράφος καταστάσεων που σχεδιάσαµε στο Μάθηµα 1.1 είναι στο σχήµα 3,
ενώ στο σχήµα 2 φαίνεται η ευρετική συνάρτηση για την εκτιµώµενη
κατανάλωση ενέργειας του Robbie για να κάνει την µετάβαση από κάθε κόµβο
ως τον κόµβο-στόχο G.

64. 64∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Σχήµα 2 Εκτιµώµενη κατανάλωση ενέργειας του Robbie.
Σχήµα 3: Ο γράφος καταστάσεων του λαβυρίθου του Robbie:

65. 65∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
(Α) Εκτελέστε τον άπληστο αλγόριθµο µε αφετηρία το S και προορισµό το G

66. 66∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
(B) Εκτελέστε τον αλγόριθµο UCS µε αφετηρία το S και προορισµό το G

67. 67∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
(Γ) Εκτελέστε τον αλγόριθµο Α* µε αφετηρία το S και προορισµό το G

68. Γ. Ασκήσεις
Εφαρµογή 2
68∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
Ο Robbie, το ροµπότ του παρακάτω σχήµατος-χάρτη, κατά τη διάρκεια των
εργασιών που κάνει διαπιστώνει ότι πρέπει να γυρίσει όσο το δυνατόν πιο γρήγορα,
από την τρέχουσα θέση S, στην κινητή βάση ανεφοδιασµού, στη θέση G,
προκειµένου να φορτίσει τις µπαταρίες του. Ο Robbie µπορεί να πλοηγηθεί
σύµφωνα µε τα βέλη του χάρτη. Πάνω σε κάθε βέλος υπάρχει ένας αριθµός που
αντιπροσωπεύει την απόσταση µεταξύ των συνδεόµενων κόµβων. Κάθε κόµβος
χαρακτηρίζεται από ένα γράµµα. ∆ίπλα στο γράµµα κάθε κόµβου βρίσκεται ένας
αριθµός που αντιπροσωπεύει την ευθεία απόσταση του κόµβου από τον κόµβο G.
Αγνοείστε προς το παρόν το διακεκοµµένο βέλος.
O Robbie διαθέτει µνήµη στην οποία έχουν καταχωρηθεί τα στοιχεία του χάρτη. Ο Robbie
αποφασίζει να βρει την καλύτερη διαδροµή χρησιµοποιώντας διάφορους αλγορίθµους, όπως
παρακάτω. Κατά την εκτέλεση των αλγορίθµων χρησιµοποιούµε τις εξής συµβάσεις σε
περιπτώσεις ισότιµων κόµβων (εκτός αν αναφέρεται διαφορετικά):
• Όταν ισότιµοι κόµβοι βρίσκονται στο ίδιο βάθος (επίπεδο) επιλέγεται ο ευρισκόµενος
αριστερότερα.
• Όταν ισότιµοι κόµβοι βρίσκονται σε διαφορετικό βάθος (επίπεδο) επιλέγεται ο ευρισκόµενος
σε µικρότερο βάθος (υψηλότερα στο δέντρο).

69. 69∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
S,9
A,8 B,6
C,5
E,3 I,2
G,0
F,1
2
2
2
3
2
1
3
2
2
2
4
H,8 D,4
3

70. 70∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
α. Κατά βάθος αναζήτηση.
Α. Να σχεδιάσετε το (τµήµα από το) δέντρο αναζήτησης που θα παραχθεί κατά την
εκτέλεση του αλγορίθµου της κατά βάθος αναζήτησης (depth-first search), αν ο Robbie
αποφασίσει να κινείται όλο αριστερά. Καταγράψτε το µονοπάτι της λύσης και υπολογίστε
το κόστος του. Καταγράψτε την σειρά επέκτασης των κόµβων και υπολογίστε πόσα
βήµατα έκανε ο αλγόριθµος.
Β. Να κάνετε το ίδιο, αν ο Robbie αποφασίσει να κινείται όλο δεξιά.

71. 71∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
β. Κατά πλάτος αναζήτηση.
Να σχεδιάσετε το (τµήµα από το) δέντρο αναζήτησης που θα παραχθεί κατά την
εκτέλεση του αλγορίθµου της κατά πλάτος αναζήτησης (breadth-first search).
Καταγράψτε το µονοπάτι της λύσης και υπολογίστε το κόστος του. Καταγράψτε την σειρά
επέκτασης των κόµβων και υπολογίστε πόσα βήµατα έκανε ο αλγόριθµος.

72. 72∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
γ. Άπληστη Αναζήτηση.
Να σχεδιάσετε το (τµήµα από το) δέντρο αναζήτησης που θα παραχθεί κατά την εκτέλεση του
αλγορίθµου της άπληστης αναζήτησης (greedy search), η οποία αναπτύσσει κάθε φορά τον κόµβο
που απέχει λιγότερο από τη θέση ανεφοδιασµού. Καταγράψτε το µονοπάτι της λύσης και
υπολογίστε το κόστος του. Καταγράψτε την σειρά επέκτασης των κόµβων και υπολογίστε πόσα
βήµατα έκανε ο αλγόριθµος.

73. 73∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
δ. Αναζήτηση µε βάση το κόστος διαδροµής.
Να σχεδιάσετε το (τµήµα από το) δέντρο αναζήτησης που θα παραχθεί κατά την εκτέλεση του
αλγορίθµου της αναζήτησης µε βάση το κόστος της διαδροµής (branch and bound search), η οποία
αναπτύσσει κάθε φορά τον κόµβο που το κόστος της διαδροµής από την αρχική θέση µέχρι αυτόν
είναι το µικρότερο. Καταγράψτε το µονοπάτι της λύσης και υπολογίστε το κόστος του. Καταγράψτε
την σειρά επέκτασης των κόµβων και υπολογίστε πόσα βήµατα έκανε ο αλγόριθµος.

74. 74∆ηµήτρης Ψούνης, ΠΛΗ31, Μάθηµα 1.3: Ευρετική Αναζήτηση
ε. Αναζήτηση µε τον Α*.
Να σχεδιάσετε το (τµήµα από το) δέντρο αναζήτησης που θα παραχθεί κατά την εκτέλεση του
αλγορίθµου Α*. Καταγράψτε το µονοπάτι της λύσης και υπολογίστε το κόστος του. Καταγράψτε την
σειρά επέκτασης των κόµβων και υπολογίστε πόσα βήµατα έκανε ο αλγόριθµος.