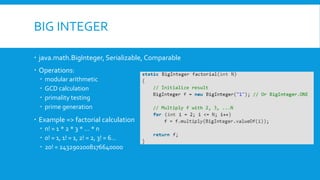
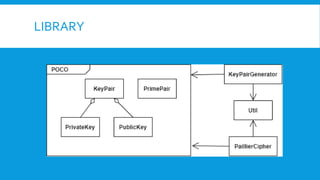
The document discusses the Paillier cryptosystem, a homomorphic encryption method allowing calculations on encrypted data while preserving the encrypted form of results. It covers its basic properties, key generation, encryption, and decryption processes, alongside its application in secure cloud computation and database queries. Additionally, it raises considerations regarding key management and performance of algorithms involved.

1. PAILLIER CRYPTOSYSTEM
Dejan Radić

2. HOMOMORPHIC ENCRYPTION
 Perform calculations on encrypted data without decrypting it first
 Result is also in encrypted form
 When result is decrypted, it is the same as if calculations had been performed on
unencrypted data
 Data at rest, data in communication… data in use?
 Cloud outsourced data computation
 Partial and Full
 f(Enc(m)) = Enc(f(m))
 A + B = Dec(Enc(A) + Enc(B))
 Performance !?

4. BACKGROUND INFO
 Pascal Paillier
 1999
 Public-Key Cryptosystems Based on Composite Degree Residuosity Classes
 Public-Key !?
 Comparable to RSA
 A
 Ciphertext addition
 Multiplication of ciphertext by plaintext

5. GREATEST COMMON DIVISOR - GCD
 Largest positive integer that divides each of the integers
 A and B are coprime numbers if gcd(A, B) = 1
 Algorithms:
 Prime factorization
 Euclid
 Least common multiple – LCM
 Smallest positive integer divisible by A and B

6. BIG MOD ALGORITHM
 Modular arithmetic
 Calculate a^p mod n where a and p are big numbers
 Overflow !?
What is the complexity
of this algorithm?

7. MODULAR MULTIPLICATIVE INVERSE
 MMI of integer a is integer x such that a*x is congruent to 1 with modulus m
 Reminder after dividing a*x with m is 1 => m divides a*x - 1
 A

8. BIG INTEGER
 java.math.BigInteger, Serializable, Comparable
 Operations:
 modular arithmetic
 GCD calculation
 primality testing
 prime generation
 Example => factorial calculation
 n! = 1 * 2 * 3 * … * n
 0! = 1, 1! = 1, 2! = 2, 3! = 6…
 20! = 2432902008176640000

9. LIBRARY

10. KEY GENERATION

11. ENCRYPTION
 BigInteger encrypt(PublicKey pub, BigInteger message)
 Check range 0<=m<n
 g^m and r^n are very large numbers !?
 Big mod algorithm
 a = g.modPow(m, n^2)
 b = r.modPow(n, n^2)
 c = a.multiply(b).mod(n^2)

12. DECRYPTION
 BigInteger decrypt(KeyPair kp, BigInteger c)
 Both private and public key needed => KeyPair
 Check range 0<c<n^2
 Recalculation => reason why Util class exists
 Lambda is part of private key

13. HOMOMORPHIC PROPERTIES
 Addition of two ciphertexts:
public static BigInteger addition(BigInteger a, BigInteger b, PublicKey pubKey) {
BigInteger n = pubKey.getN();
BigInteger n_sqr = n.multiply(n);
return a.multiply(b).mod(n_sqr);
}
 Multiplication of a ciphertext by a plaintext:
public static BigInteger multiplication(BigInteger a, int b, PublicKey pubKey) {
BigInteger n = pubKey.getN();
BigInteger n_sqr = n.multiply(n);
return a.pow(b).mod(n_sqr);
}

14. OBLIVIOUS AGGREGATE QUERY USE CASE
 Average of n numbers:
 n-1 additions (x2)
 Single division
 Database (sum and count), proxy (division)
 Problems:
 Key management
 Multiplication aggregate => EXP(SUM(LOG(column)))
 Large numbers => binary, varbinary

15. HOW TO CODE DECIMALS
INSTEAD OF INTEGERS?

16. QUESTIONS ?
Thank you for your attention!