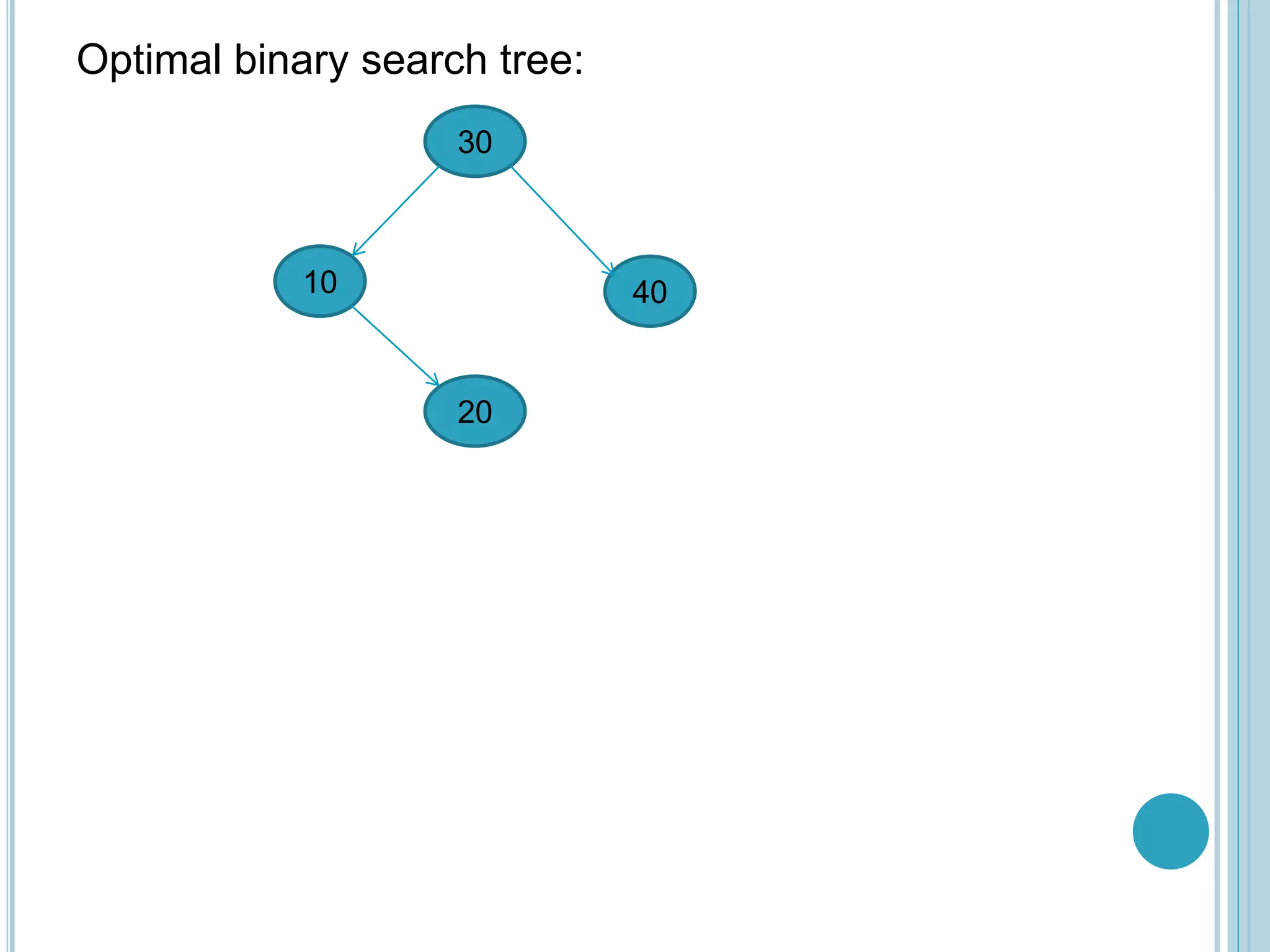
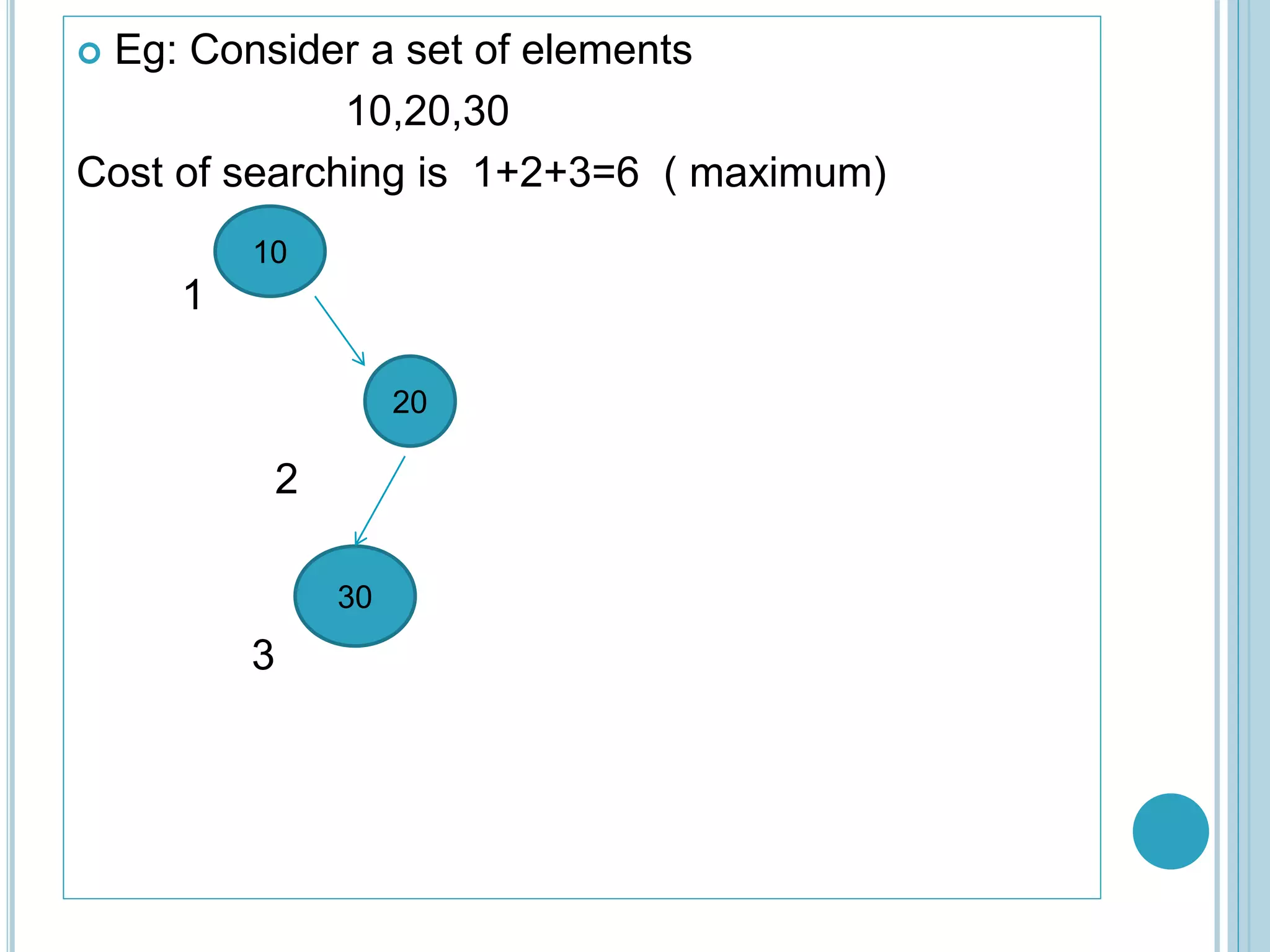
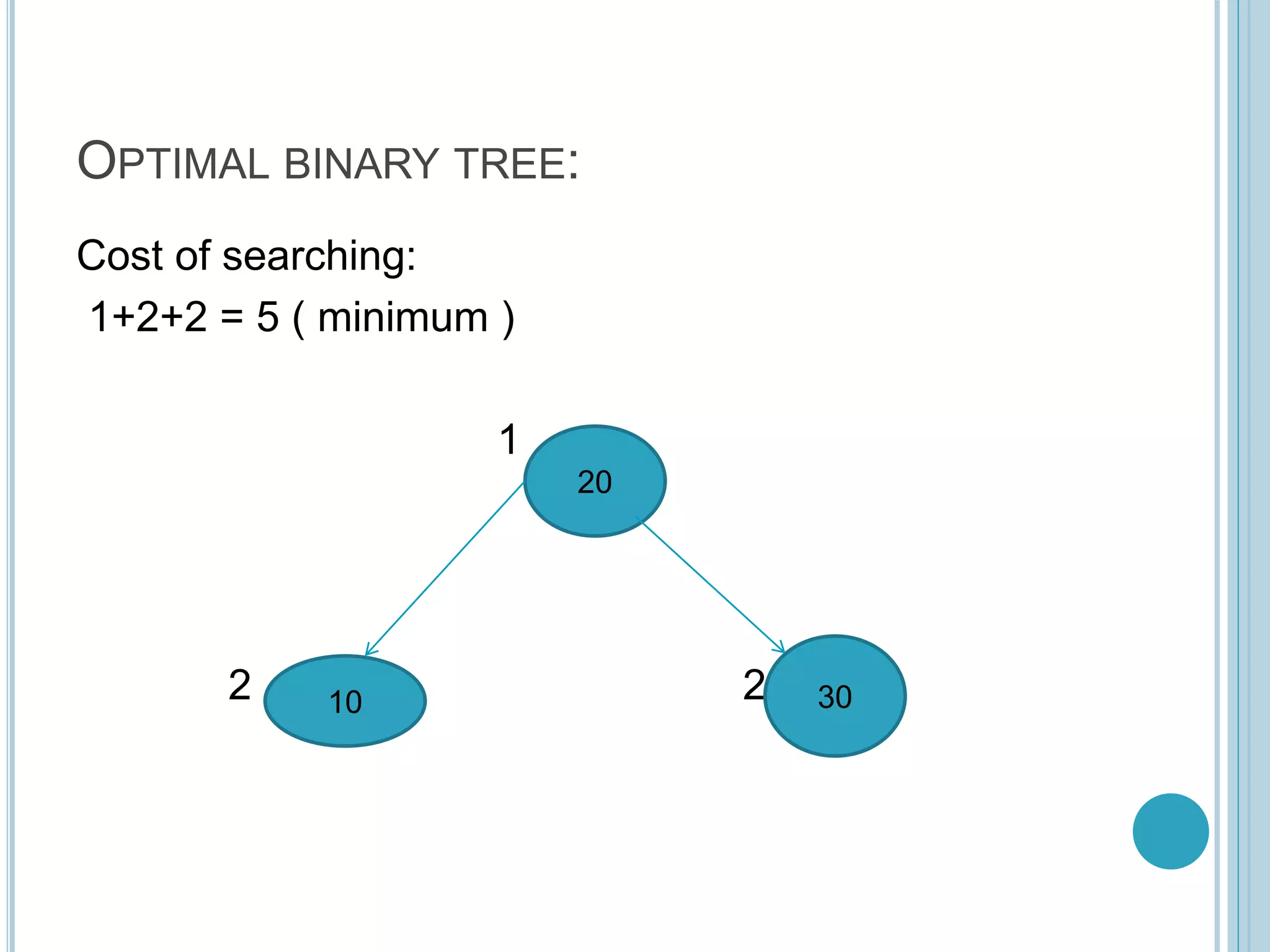
The document discusses optimal binary search trees. It begins by defining binary trees and binary search trees, noting that binary search trees require that left child nodes be less than the parent and right child nodes be greater. It then explains that an optimal binary search tree arranges elements in a binary structure to minimize search costs. The document provides an example comparing search costs between different binary tree structures. It outlines the optimal binary search tree algorithm, which calculates costs c[i,j] of reaching nodes i through j recursively to find the lowest cost tree structure.

1. DESIGN ANALYSIS AND
ALGORITHM
TOPIC : OPTIMAL BINARY SEARCH TREE

2. BINARY TREE
 Each parent node has atmost two child nodes.
 It has parent node and 2 leaf nodes
 This is called a binary tree.
 Eg:
2
7 5
3 6 3 8

3. BINARY SEARCH TREE
 EXAMPLE :
8
3 10
1 6
14

4. BINARY SEARCH TREE ( CONT..)
 Left child values should be less than the parent
node or Root node.
 Right child values should be greater than Root
Node.
 This is called Binary search tree.

5.  For the purpose of searching we have a different
types of searches.
 Linear search
 Binary search
 Binary tree data structure.

6. BINARY TREE DATA STRUCTURE
 Binary tree is mainly used for searching purpose
also and it is very easy to identify the elements.
 For searching an element in binary tree,the
maximum time is taken, when the element is
present in a leaf.
 The height of the binary tree is log n.
 In order to rectify the cost of search we are using
optimal binary search tree.

7. OPTIMAL BINARY SEARCH TREE
 The arrangement of elements in the form of a
binary data structure such that the cost of searching
the elements is minimum.
 This is called optimal binary search tree.
 To reduce the cost of searching we use optimal
binary search tree.
 The word “optimal” means best so , to search an
element we use the best way that is optimal binary
search tree.

8.  Eg: Consider a set of elements
10,20,30
Cost of searching is 1+2+3=6 ( maximum)
1
2
3
10
20
30

9. OPTIMAL BINARY TREE:
Cost of searching:
1+2+2 = 5 ( minimum )
1
2 2
20
10 30

10. 0 4 81 203 263
0 2 103 163
0 6 123
0 3
0
0 1 2 3 4
0
1
2
3
4
i
j

11.  Step 1: Consider the cost of reaching the same node
 c[0,0]=0
 c[1,1]=0
 c[2,2]=0
 c[3,3]=0
 C[4,4]=0
Step2: Consider the cost of reaching one node
• c[0,1]=4
• c[1,2]=2
• c[2,3]=6
• c[3,4]=3

12.  Step 3: Consider cost of reaching 2 nodes distance
 c[0,2], c[1,3] , c[2,4]
 c[i,j]= min{ c[i,k-1] + c[k,j] + w[i,j]}
 Where k=1 ( rootnode)
 c[0,2]= min { c[0,0]+c[1,2]+w[0,2],c[0,1]+c[2,2]+w[0,2]}
 =min{ 0+2+6, 4+0+6}
 =min{8,10}
 C[0,2]=81
 c[1,3]= min { c[1,1]+c[2,3]+w[1,3],c[1,2]+c[3,3]+w[1,3]}
 =min{ 0+6+8,2+0+8}
 =min{14,10}
 C[1,3]=103

13.  c[2,4]= min { c[2,2]+c[3,4]+w[2,4],c[2,3]+c[4,4]+w[2,4]}
 =min{ 0+3+9, 6+0+9}
 =min{12,15}
 C[2,4]=123
 Step 4: Consider the cost of reaching 3 nodes.
 c[0,3]= min {
c[0,0]+c[1,3]+w[0,3],c[0,1]+c[2,3]+w[0,3],c[0,2]+c[3,3]+12}
 =min{ 0+10+12,4+6+12,8+0+12}
 =min{22,22,20}
 C[0,3]=203

14.  c[1,4]= min {
c[1,1]+c[2,4]+w[1,4],c[1,2]+c[3,4]+w[1,4],c[1,3]+
 c[4,4]+w[1,4]}
 =min{ 0+12+11,2+3+11,10+0+11}
 =min{23,16,21}
 C[1,4]=163
 Step 5: Consider the cost of reaching 4 nodes.
 c[0,4]= min {
c[0,0]+c[1,4]+w[0,4],c[0,1]+c[2,4]+w[0,4],c[0,2]+c[3,
4]+w[0,4],c[0,3]+c[4,4]+w[0,4]}
 =min{ 31,31,26,35}
 =min{22,22,20}
 C[0,4]=263

15. Optimal binary search tree:
10 40
20
30

16. THANK YOU