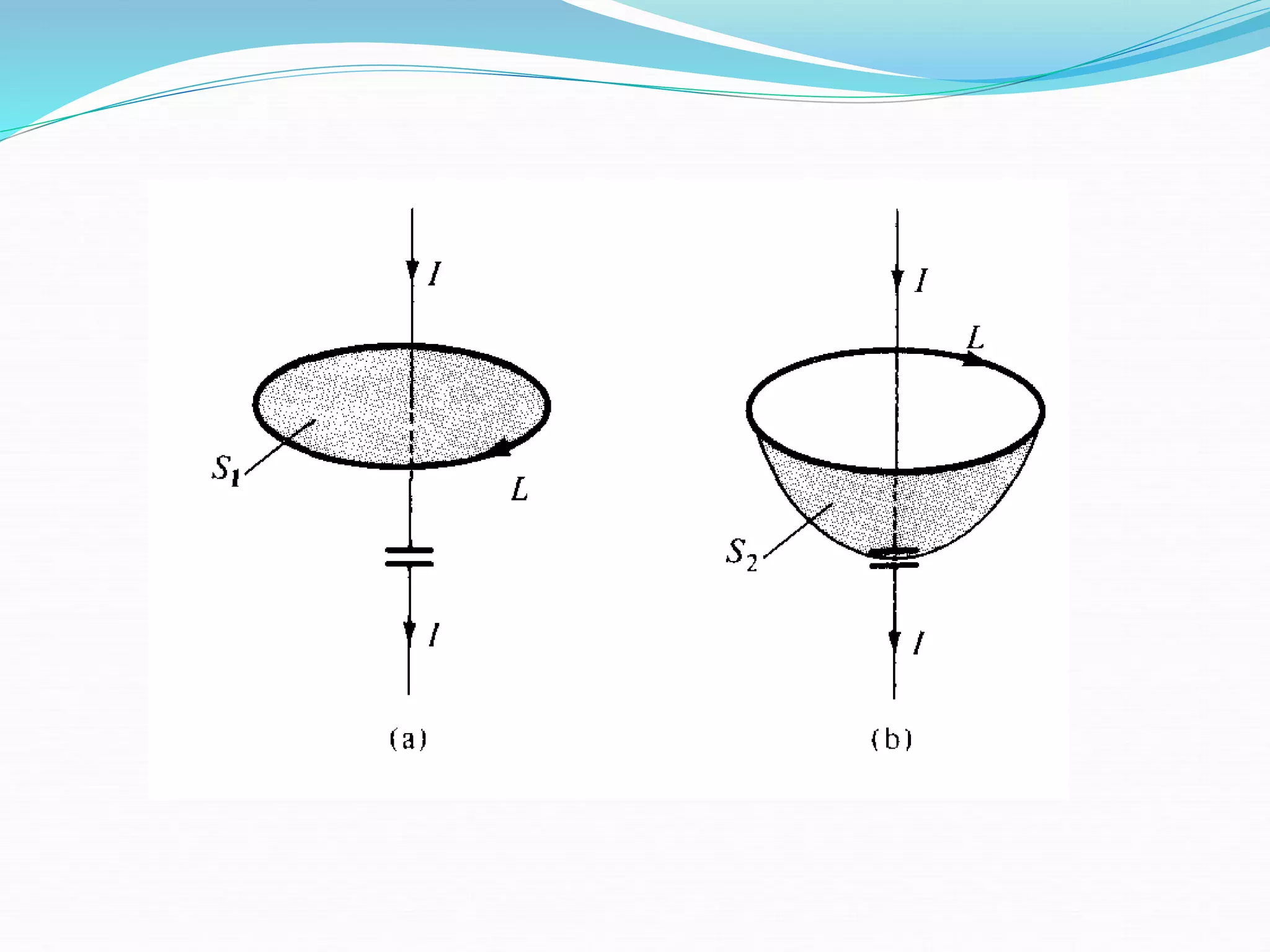
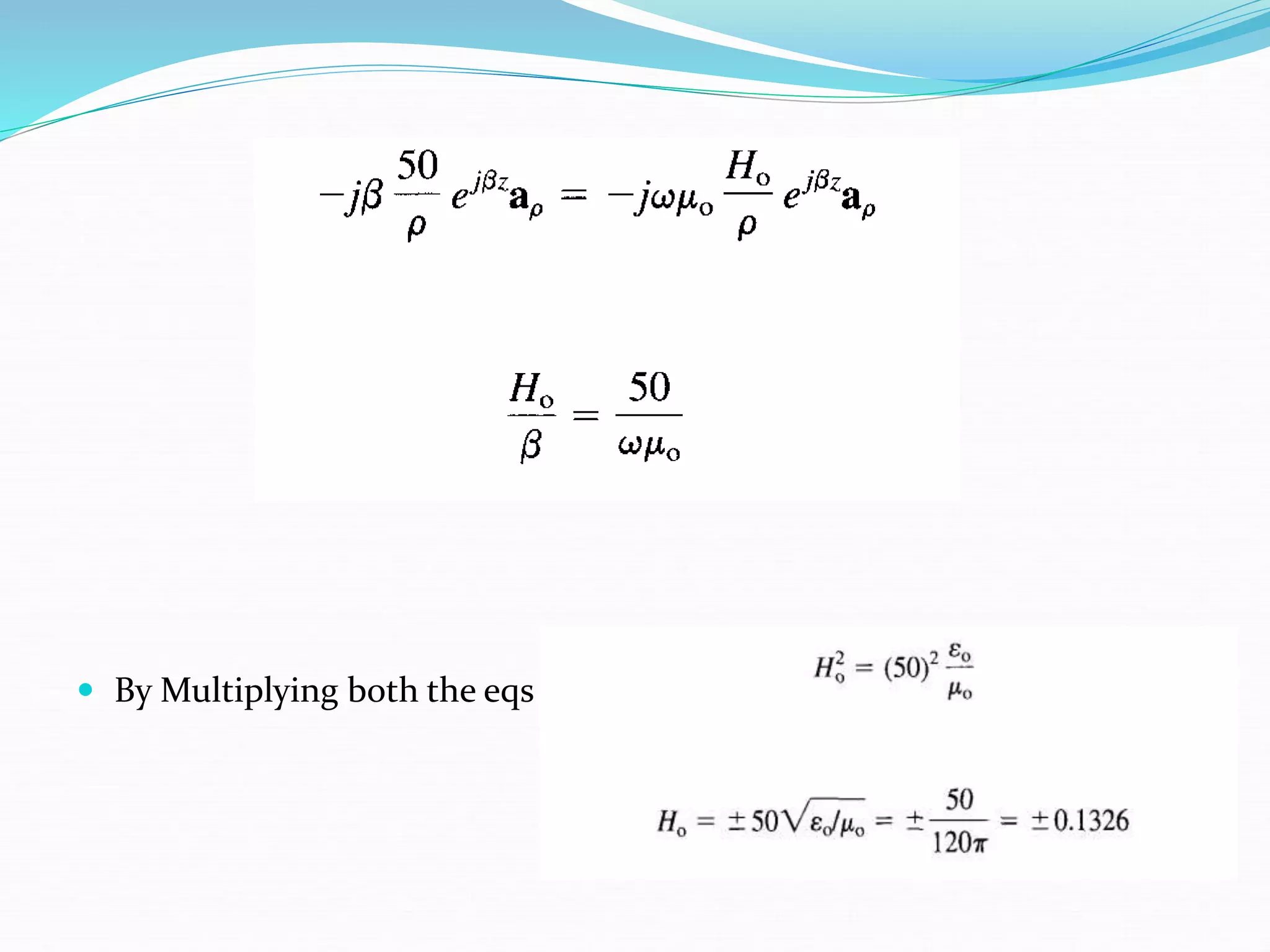
This document discusses Maxwell's equations and displacement current. It begins by introducing two textbooks on electromagnetics as references. It then explains that Maxwell modified Ampere's law for time-varying magnetic fields by adding a term for displacement current density, defined as the time derivative of electric displacement. This resolved inconsistencies between Ampere's law and Faraday's law for time-varying fields. The displacement current allows the total current in a closed path to be the same whether calculated from conduction current through one surface or displacement current through another surface.

2. Books
Text Book:
 1. PRINCIPLES OF ELECTROMAGNETICS
 By - MATTHEW N.O. SADIKU, 4th 2009 OXFORD UNIVERSITY
 PRESS, INDIA
Reference Book:
 1. ELECTROMAGNETIC WAVES AND RADIATING SYSTEMS
 By - EDWARD C. JORDAN 5th PRENTICE HALL

3. Displacement Current
 In the previous section, we have essentially reconsidered
Maxwell's curl equation for electrostatic fields and modified it
for time-varying situations to satisfy Faraday's law. We shall now
reconsider Maxwell's curl equation for magnetic fields (Ampere's
circuit law) for time-varying conditions.
 For static EM fields, we recall that
 But the divergence of the curl of any vector field is identically
zero,Hence:
 The continuity of current in eq. , however, requires that

4.  Thus both the eqs are obviously incompatible for time-varying
conditions.
 We must modify the Ampere Circuit law
 To do this, we add a term in the eq. of Amp Circuit law so that it
becomes
 Where is to be determined and defined. Again, the
divergence of the curl of any vector is zero. Hence:

5.  Substituting in equation
 This is Maxwell's equation (based on Ampere's circuit law) for a
time-varying field. The term Jd = dD/dt is known as
displacement current density and J is the conduction
currentdensity ( ).

6.  Based on the displacement current density, we define
the displacement current as
 where I is the current through the conductor and S1 is
the flat surface bounded by L.
 If we use the balloon-shaped surface S2 that passes
between the capacitor plates, as in Figure

8.  because no conduction current (J = 0) flows through S2
 This is contradictory in view of the fact that the same closed path
L is used. To resolve the conflict, we need to include the
displacement current in Ampere's circuit law. The total current
density is
 Now the equations remains valid.
 So we obtain the same current for either surface though it is
conduction current in S1 and displacement current in S2.

9. Example

12. Example

14.  Complex Number can be defined as:

21. Example

23.  Substituting this we get

24.  By Multiplying both the eqs

25.  By Dividing both the equations

26. Example

28. Example

30. Example