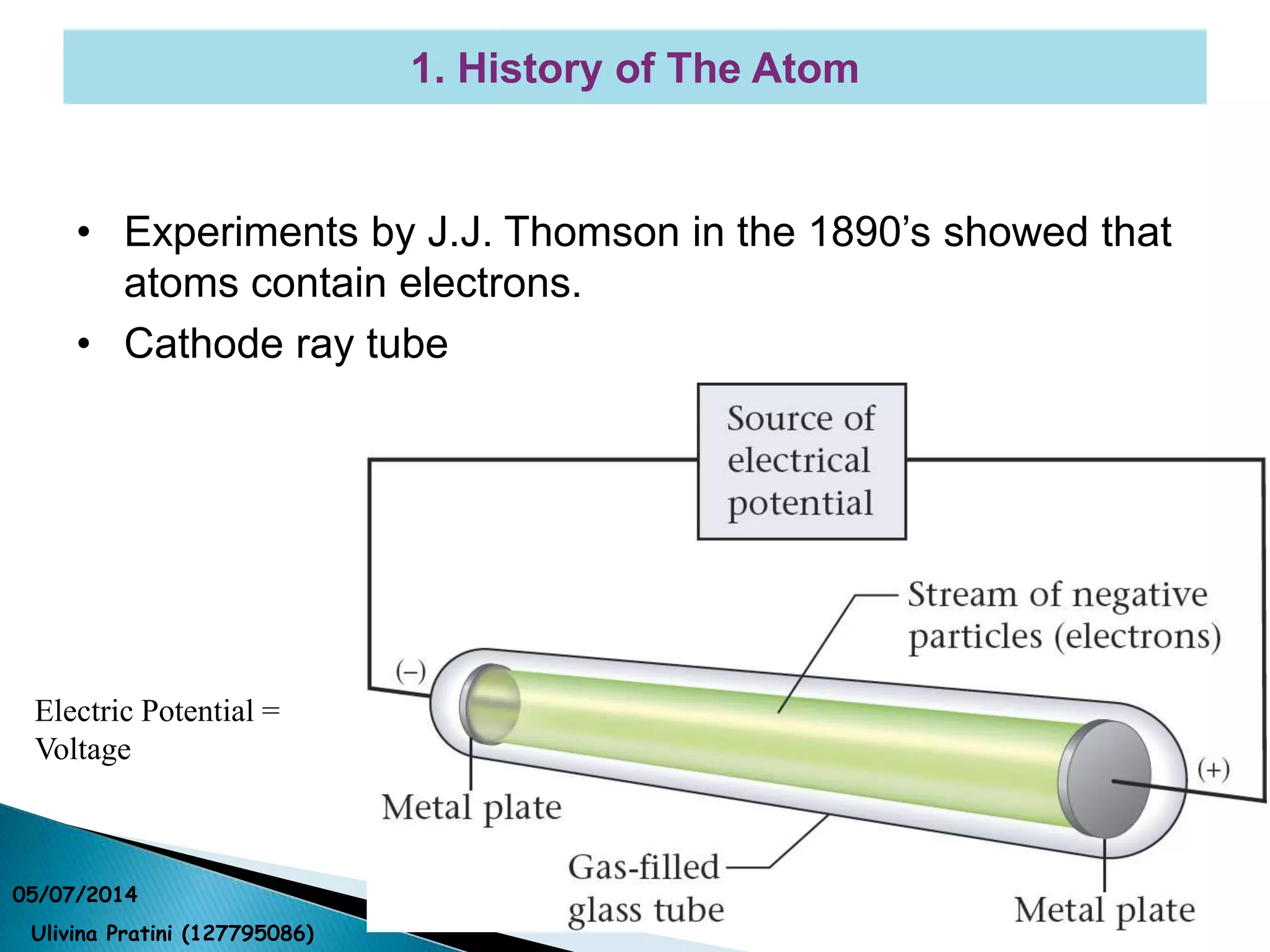
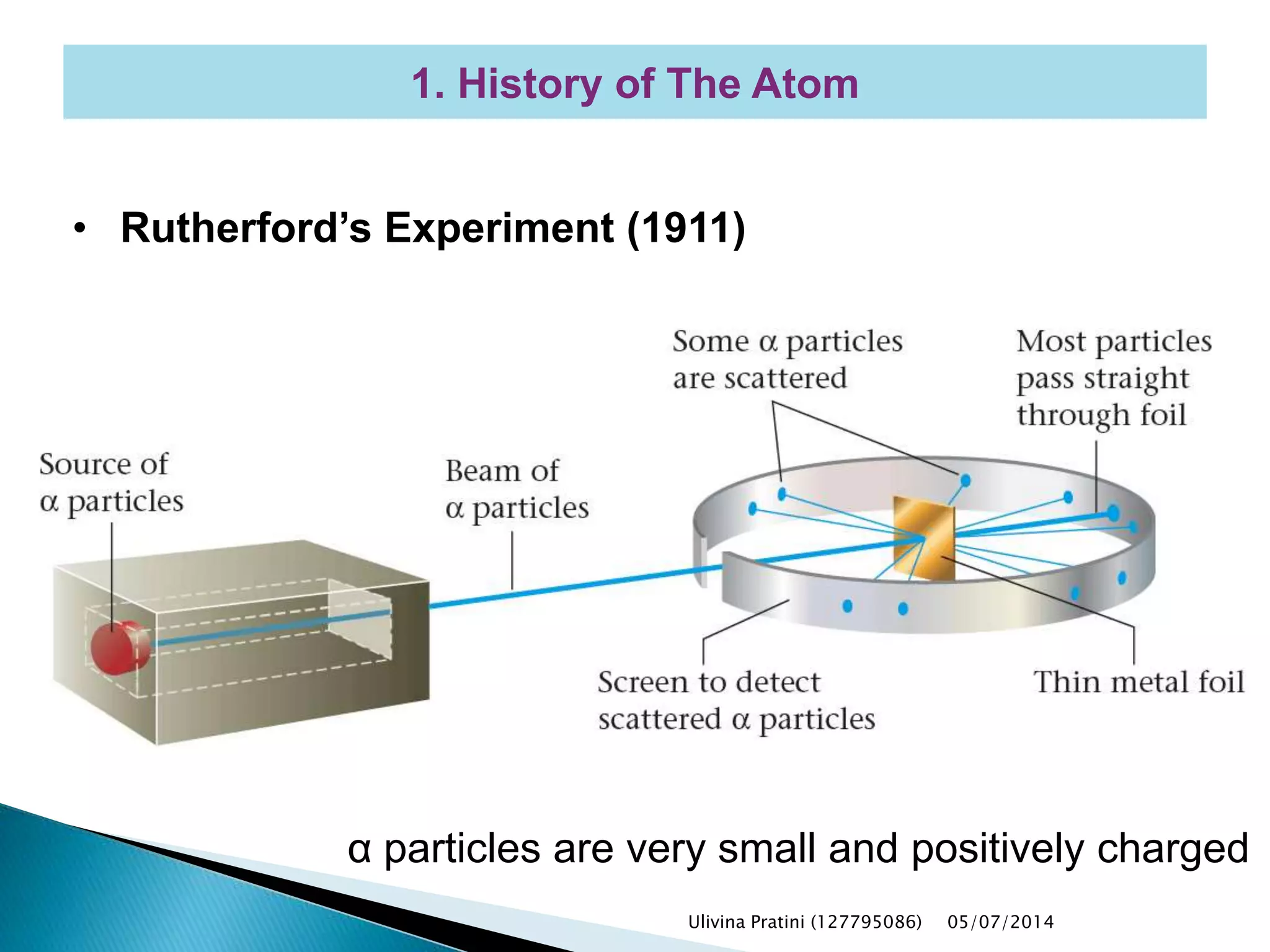
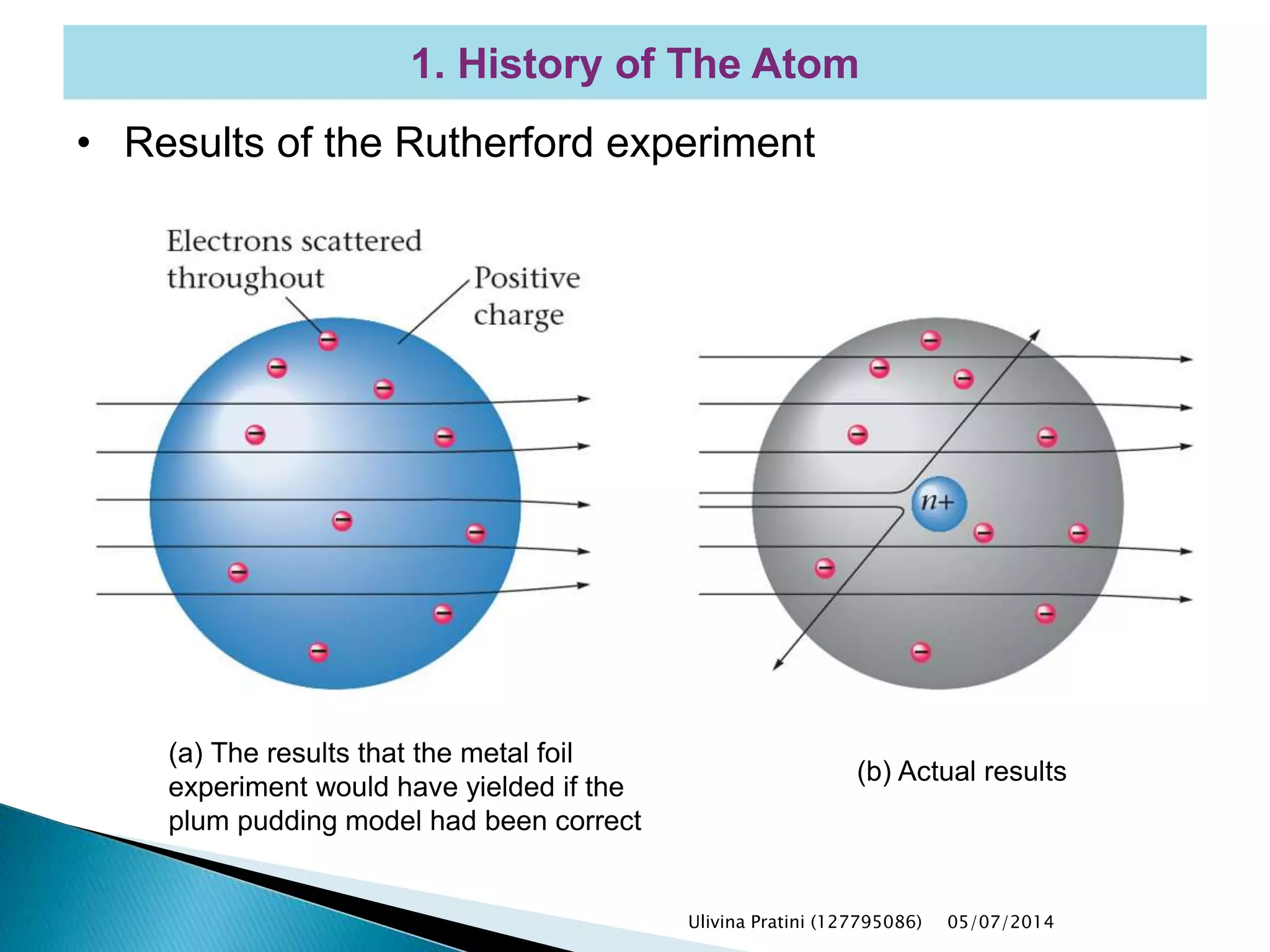
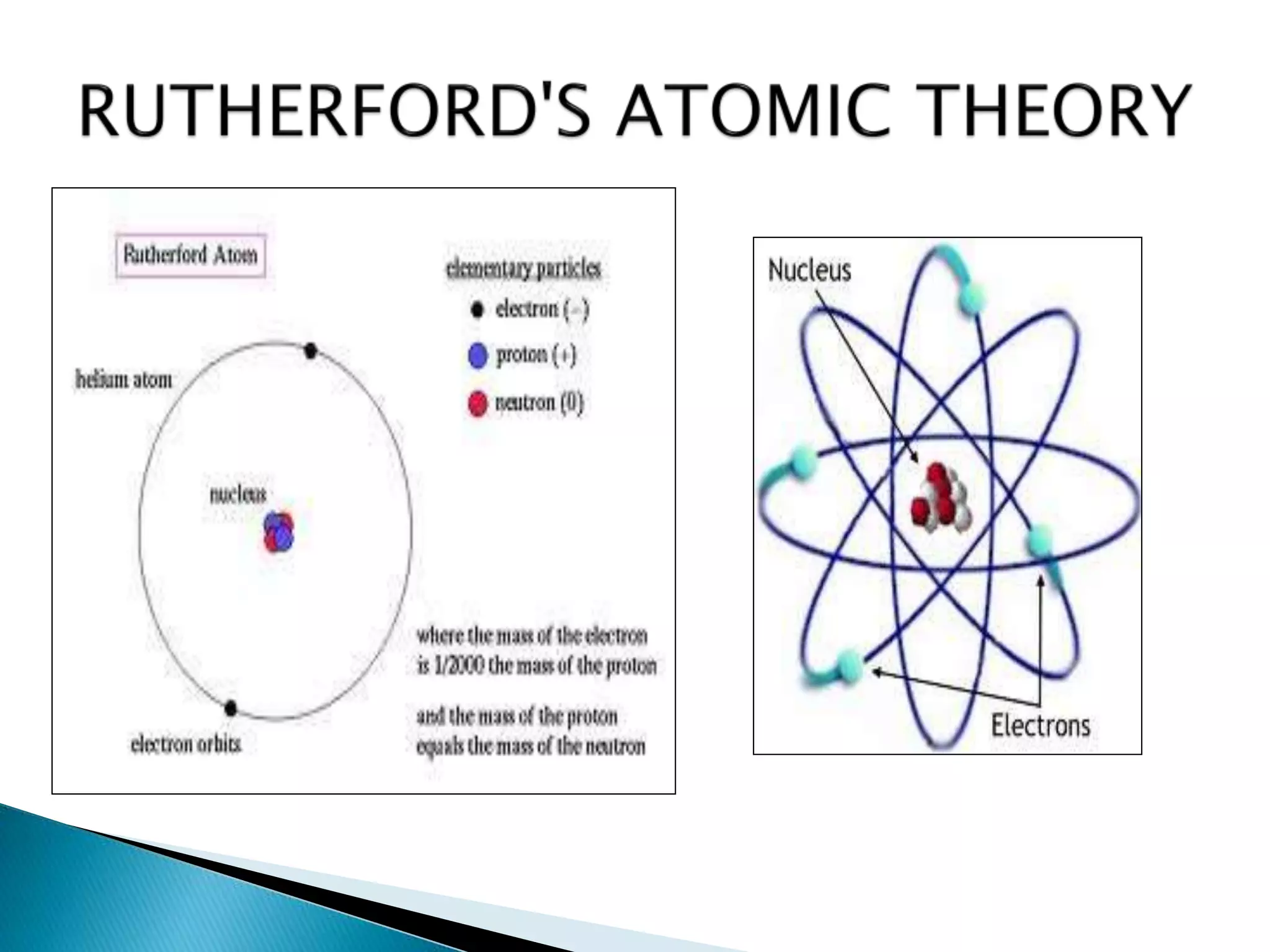
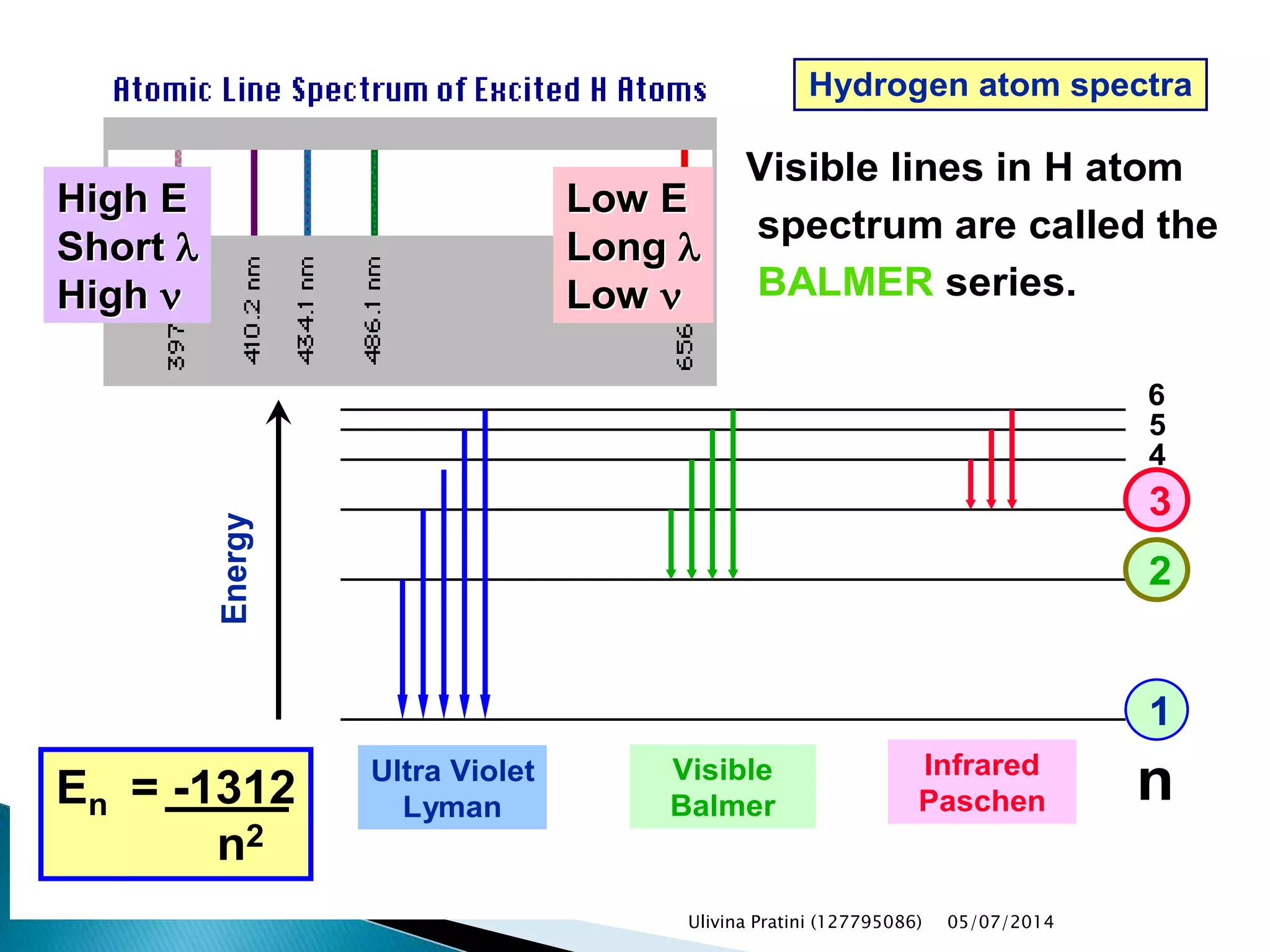
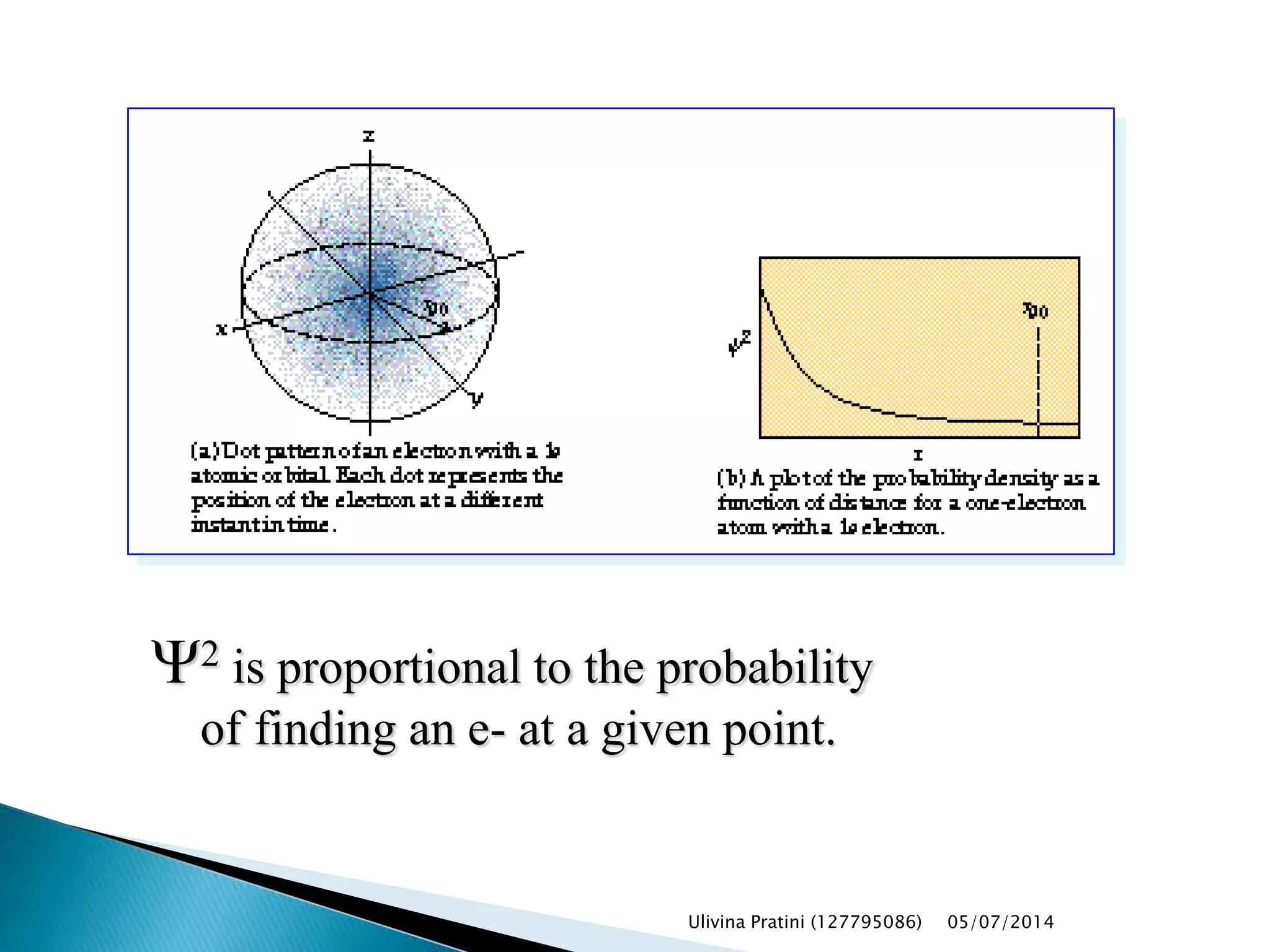
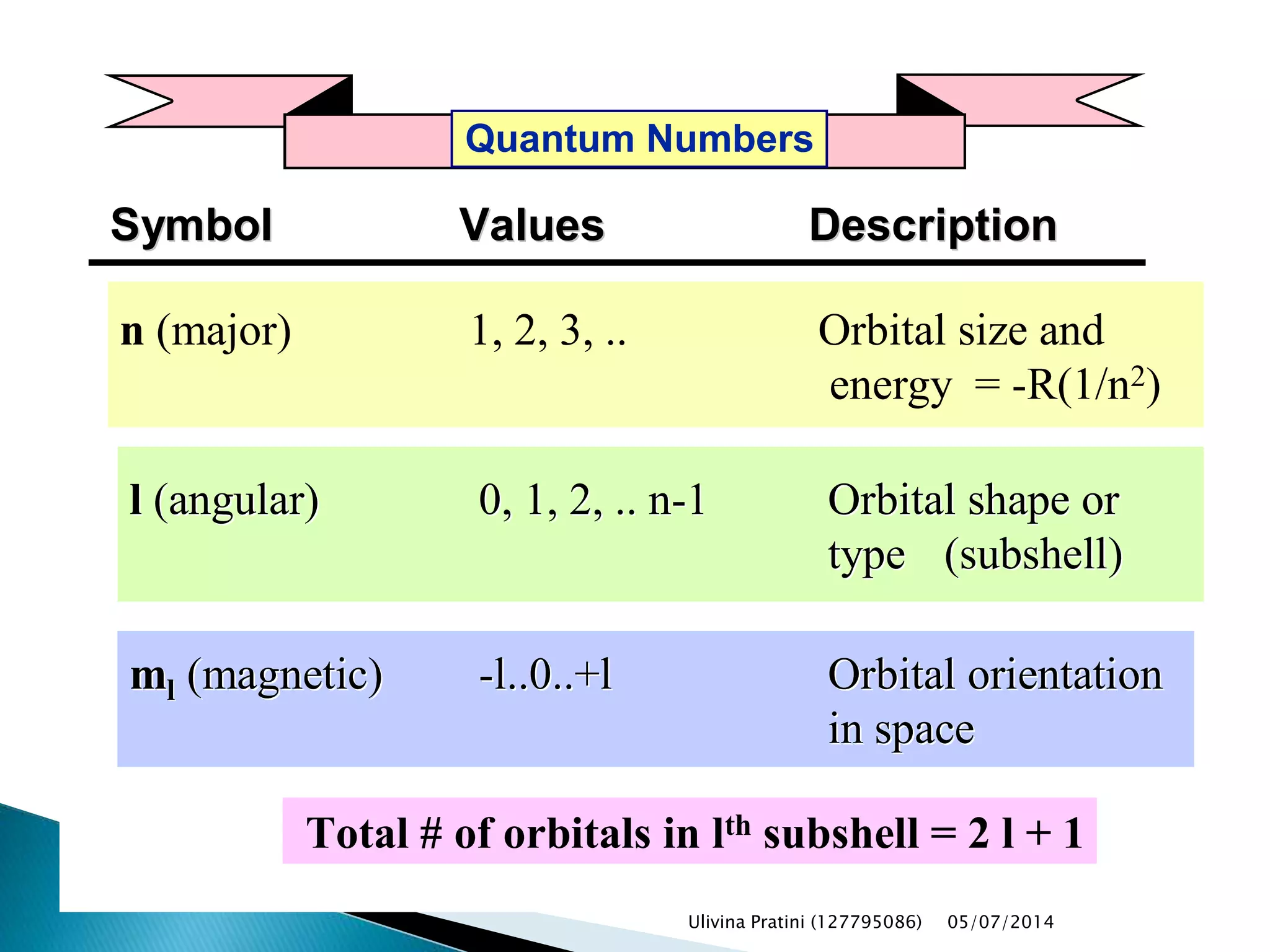
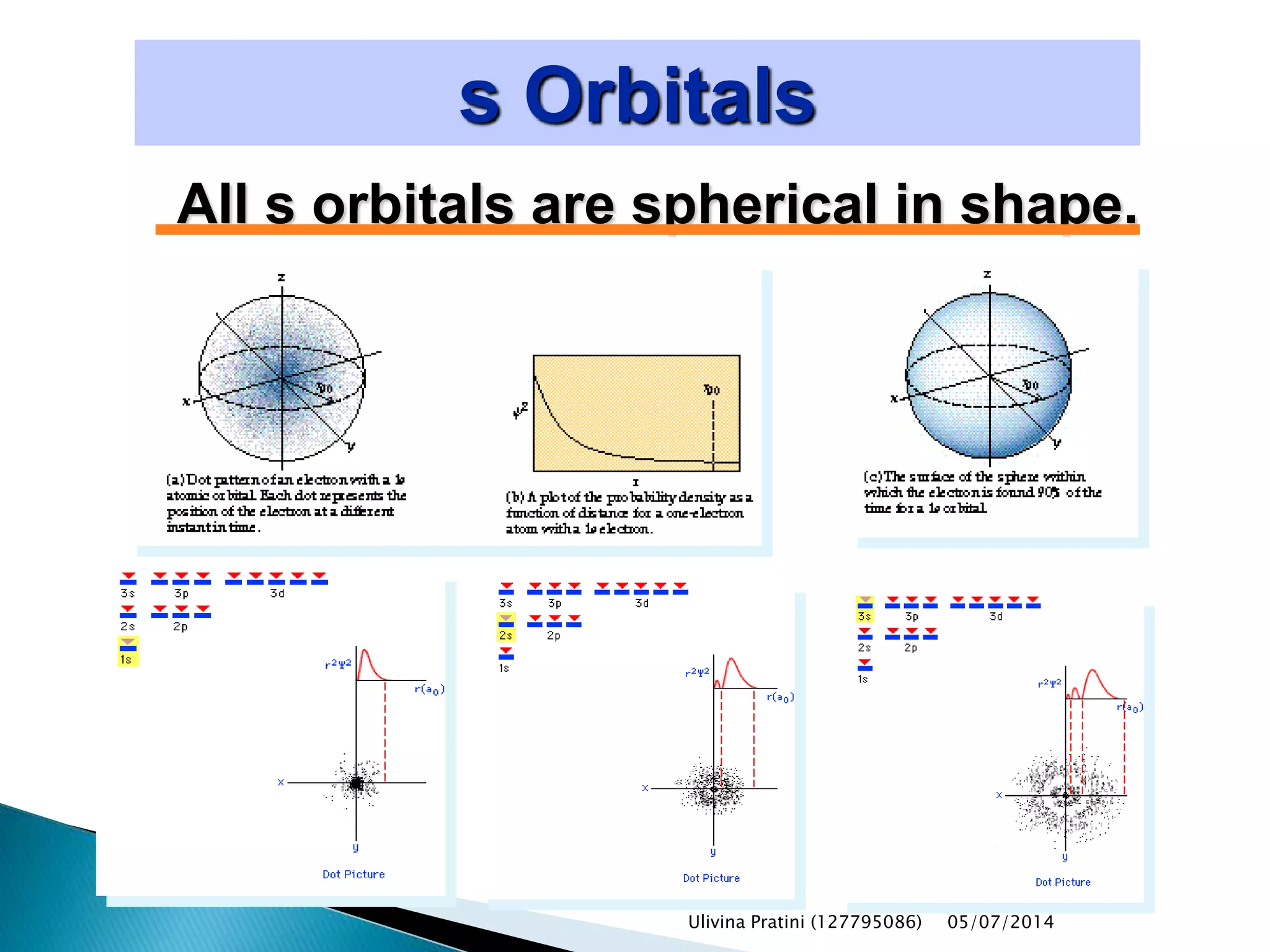
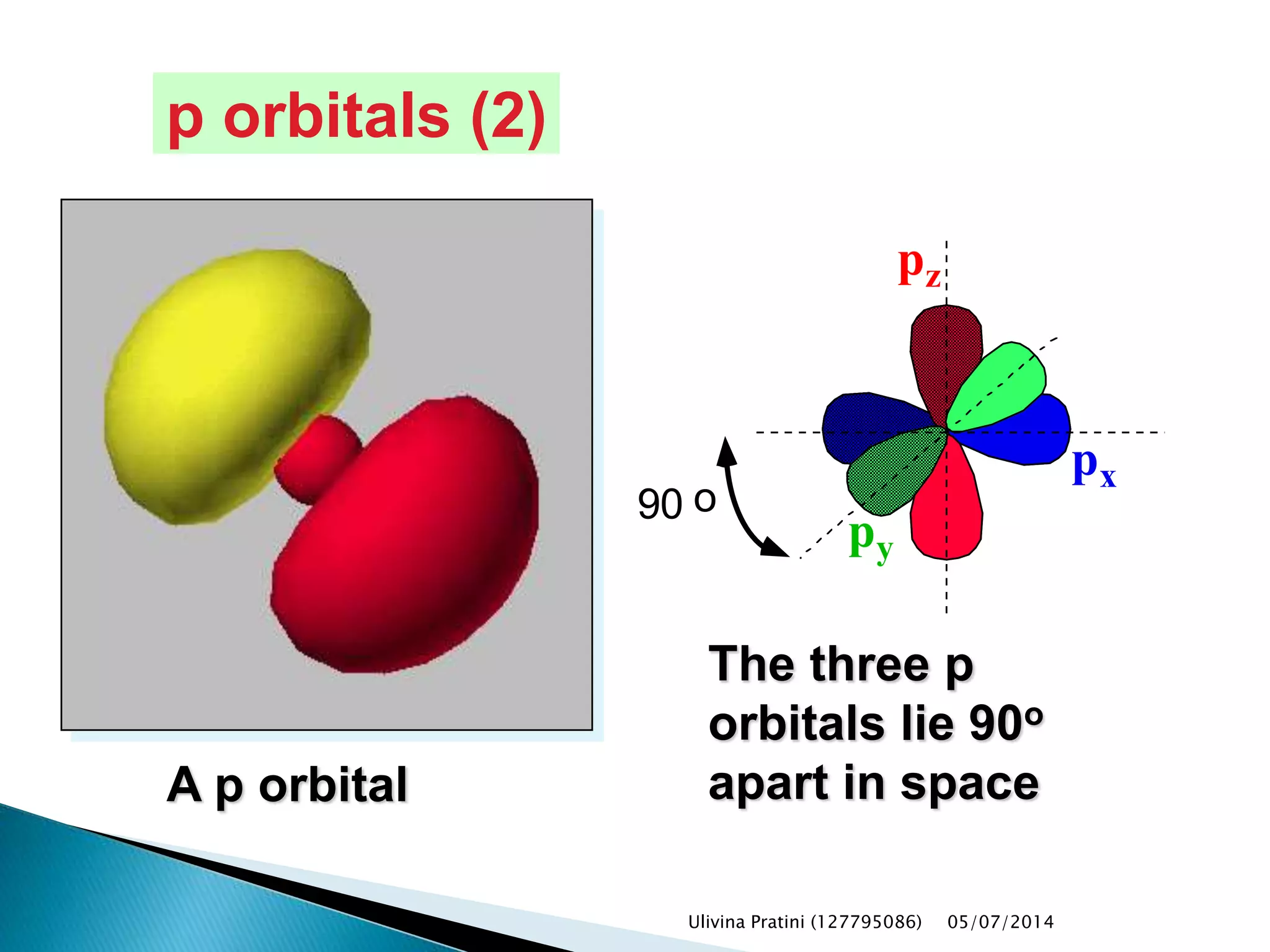
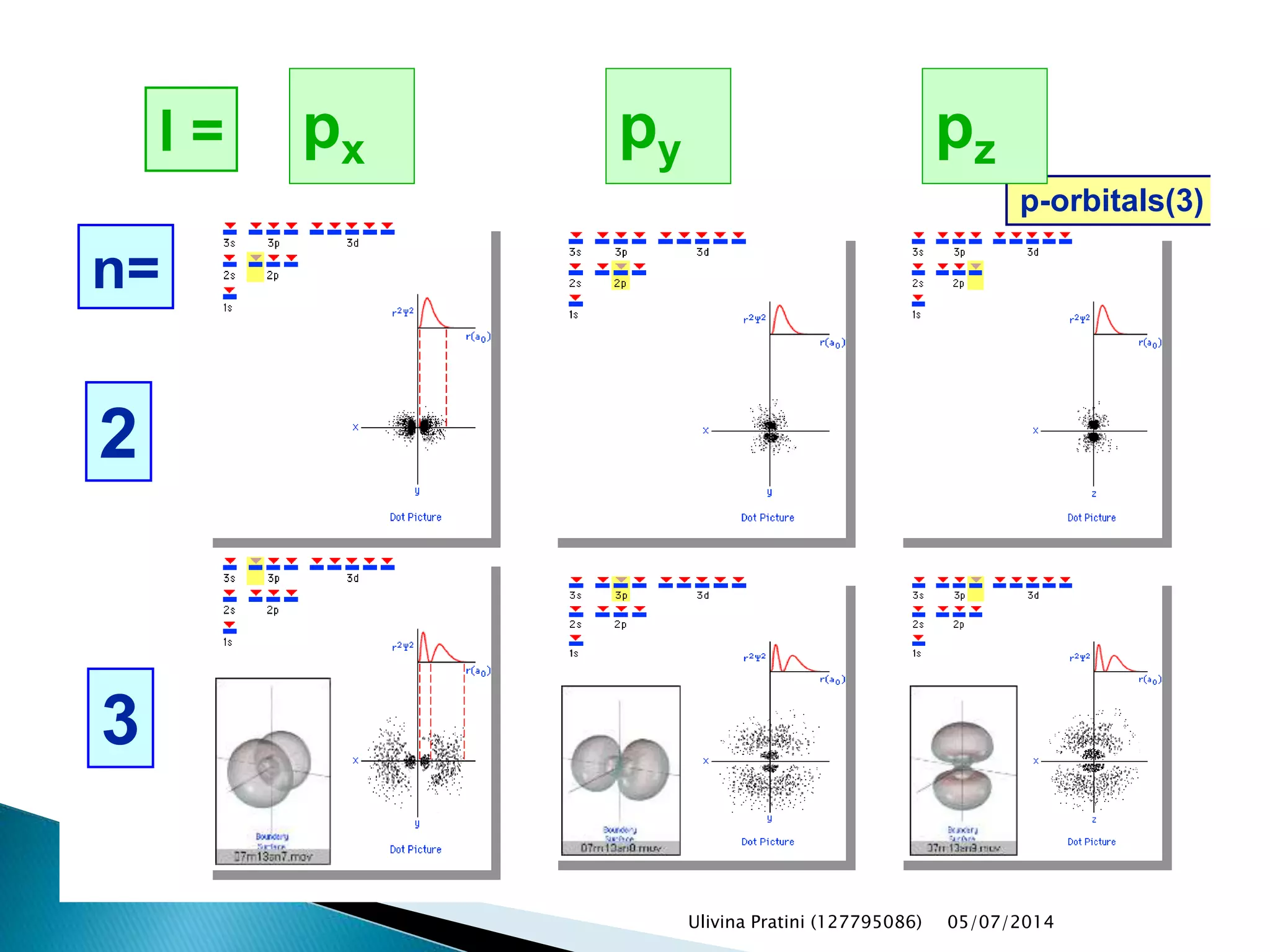
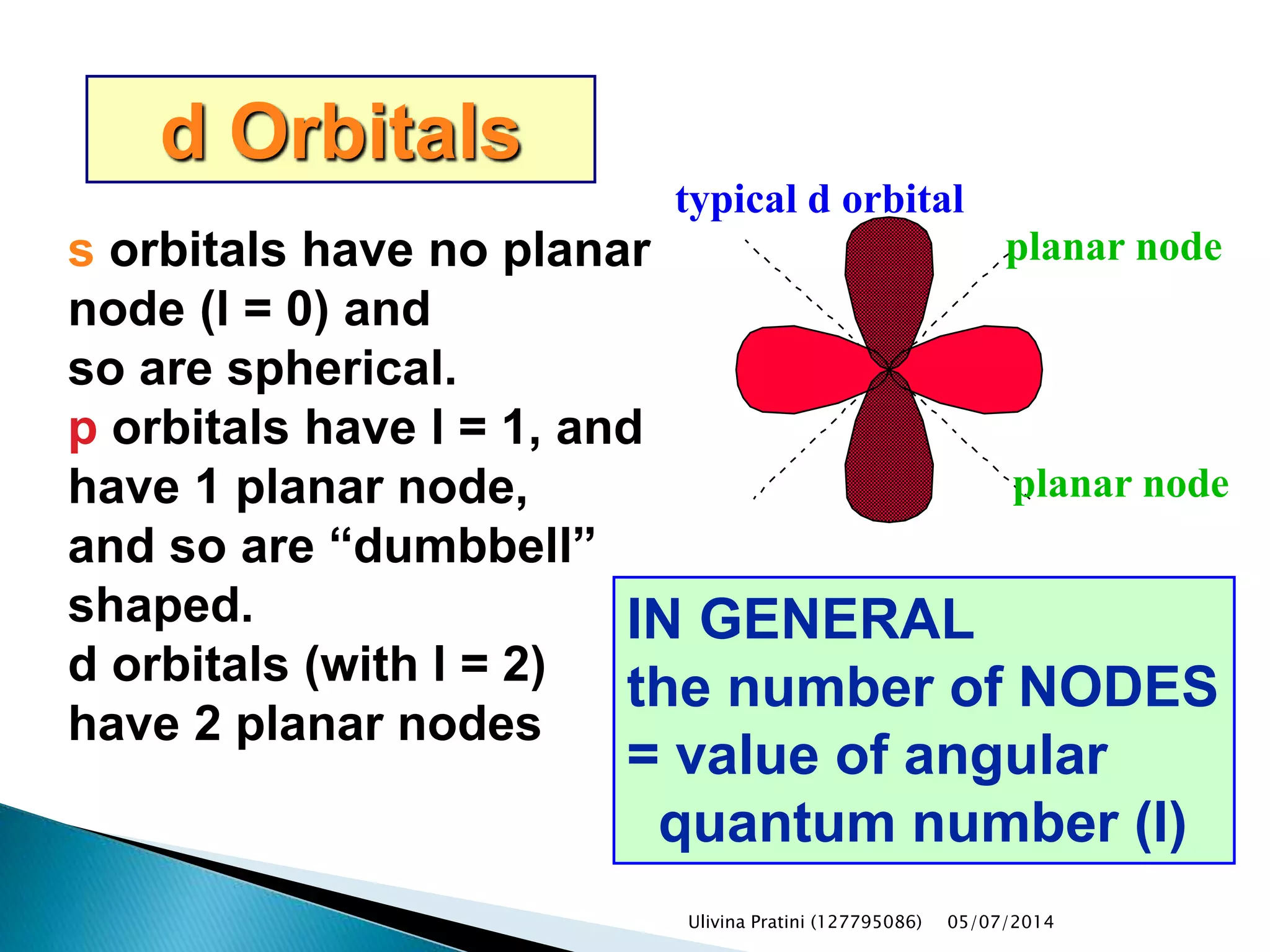
This document provides an overview of the history of atomic structure models. It begins with early Greek philosophers' concept of atoms. In the 19th century, Dalton proposed that elements are made of unique atom types that can combine. Experiments by Thomson, Rutherford and Bohr led to discoveries about the electron and nuclear structure of atoms. Bohr's 1913 model improved on Rutherford's by proposing discrete electron orbits. Later, the developments of quantum mechanics by Heisenberg, Schrodinger, de Broglie and others explained atomic structure and spectra through wave functions and quantum numbers. This allowed visualization of electron orbitals in atoms.

1. SCIENCE EDUCATION
MASTER DEGREE PROGRAM
THE STATE UNIVERSITY OF SURABAYA
ULIVINA PRATINI
(127795086)

2. Democritus, systematized his
views. In approximately 450 BC,
Democritus coined the term
átomos, which means
"uncuttable" or "the smallest
indivisible particle of matter".
1. History of The Atom

3. In 1805, English instructor and natural
philosopher John Dalton used the
concept of atoms.
He proposed that each element consists
of atoms of a single, unique type, and
that these atoms can join together to
form chemical compounds.
1. History of The Atom

4. • Experiments by J.J. Thomson in the 1890’s showed that
atoms contain electrons.
• Cathode ray tube
1. History of The Atom
Electric Potential =
Voltage
Ulivina Pratini (127795086)
05/07/2014

5. • The Plum Pudding (Chocolate Chip Cookie) Model
1. History of The Atom
Ulivina Pratini (127795086) 05/07/2014

6. • Rutherford’s Experiment (1911)
α particles are very small and positively charged
1. History of The Atom
Ulivina Pratini (127795086) 05/07/2014

7. • Results of the Rutherford experiment
(a) The results that the metal foil
experiment would have yielded if the
plum pudding model had been correct
(b) Actual results
1. History of The Atom
Ulivina Pratini (127795086) 05/07/2014

8. 1. Since most of the alpha particles were
passed through the foil undeflected,
therefore, it was concluded that most of
the atom is empty.
2. Small angles of deflection indicate that
positively charged alpha particles were
attracted by electrons.
3. Large angles of deflection indicate that
there is a massive positively charged
body present in the atom and due to
repulsion alpha particles were deflected
at large angles.

10. • Comparing the Parts of an Atom
Ulivina Pratini (127795086) 05/07/2014

11. There were two fundamental defects in
Rutherford's atomic model:
According to classical electromagnetic
theory, being a charge particle electron
when accelerated must emit energy. We
know that the motion of electron around the
nucleus is an accelerated motion,
therefore, it must radiate energy. But in
actual practice this does not happen.
Suppose if it happens then due
to continuous loss of energy orbit of
electron must decrease continuously.
Consequently electron will fall into the
nucleus. But this is against the actual
situation and this shows that atom is
unstable.
If the electrons emit energy continuously,
they should form continuous spectrum. But
actually line spectrum is obtained

12. •Bohr’s greatest contribution to
science was in building a simple
model of the atom.
• It was based on understanding
the SHARP LINE SPECTRA of
excited atoms.
Niels Bohr
(1885-1962)
(Nobel Prize,
1922)
Ulivina Pratini (127795086) 05/07/2014

13. Line Spectra of Excited Atoms
• Excited atoms emit light of only certain wavelengths
• The wavelengths of emitted light depend on the
element.
H
Hg
Ne
Ulivina Pratini (127795086) 05/07/2014

14. +
Electron
orbit
2. But a charged particle moving in an
electric field should emit energy.
1. Classically any orbit should be
possible and so is any energy.
4. Atomic Spectra and Bohr Model
One view of atomic structure in early 20th
century was that an electron (e-) traveled
about the nucleus in an orbit.
Ulivina Pratini (127795086) 05/07/2014

15. • Bohr said classical view is wrong. Need a
new theory — now called QUANTUM or
WAVE MECHANICS.
• e- can only exist in certain discrete orbit —
called stationary states.
• e- is restricted to QUANTIZED energy states.
4. Atomic Spectra and Bohr Model
Ulivina Pratini (127795086) 05/07/2014

16. 4-H_SPECTRA.MOV
H atom
07m07an1.mov
If e-’s are in quantized energy
states, then DE of states can
have only certain values. This
explains sharp line spectra.
4. Atomic Spectra and Bohr Model
Ulivina Pratini (127795086) 05/07/2014
n = 1
n = 2
E = -R (1/22)
E = -R (1/12)
R, the Rydberg constant. R = 1312 kJ/mol or 3.29 x 1015 Hz

17. Hydrogen atom spectra
Visible lines in H atom
spectrum are called the
BALMER series.
High EHigh E
ShortShort 
HighHigh 
Low ELow E
LongLong 
LowLow 
Energy
Ultra Violet
Lyman
Infrared
Paschen
Visible
BalmerEn = -1312
n2
6
5
3
2
1
4
n
Ulivina Pratini (127795086) 05/07/2014

18. 05/07/2014Ulivina Pratini (127795086)
Each stationary orbit
corresponds to a definite
energy.There stationary
orbit are designated by
K,L,M,N,O,… .The orbit
close to the nucleus has less
energy compared to the
orbit away from the
nucleus.
4. Atomic Spectra and Bohr Model

19. 05/07/2014Ulivina Pratini (127795086)
Atomic spectra display fine structure due to splitting
of spectral lines. I an attempt to account for the fine
structure, Arnold Sommerfeld proposed elliptical
orbits instead of circular orbits proposed by Bohr.
=

20. • Bohr’s theory was a great accomplishment
and radically changed our view of matter.
• But problems existed with Bohr theory —
– theory only successful for the H atom.
– introduced quantum idea artificially.
• So, we go on to QUANTUM or WAVE
MECHANICS
Ulivina Pratini (127795086) 05/07/2014

21. • Light has both wave & particle
properties
• de Broglie (1924) proposed that all
moving objects have wave
properties.
• For light: E = h = hc / 
• For particles: E = mc2 (Einstein)L. de Broglie
(1892-1987)
 for particles is called the de Broglie wavelength
and for particles
(mass)x(velocity) = h / 
Therefore, mc = h / 
Ulivina Pratini (127795086) 05/07/2014

22. 05/07/2014Ulivina Pratini (127795086)
Uncertainty Principle

23. W. Heisenberg
1901-1976
Uncertainty
Principle
Problem of defining nature of
electrons in atoms solved by W.
Heisenberg.
Cannot simultaneously define the
position and momentum (= m•v) of an
electron.
Dx. Dp = h
At best we can describe the position
and velocity of an electron by a
PROBABILITY DISTRIBUTION,
which is given by Y2
Ulivina Pratini (127795086) 05/07/2014

24. E. Schrodinger
1887-1961
Schrodinger applied idea of e- behaving
as a wave to the problem of electrons in
atoms.
Solution to WAVE EQUATION gives set of
mathematical expressions called
WAVE FUNCTIONS, Y
Each describes an allowed energy state
of an e-
Quantization introduced naturally.
Ulivina Pratini (127795086) 05/07/2014

25. WAVE FUNCTIONS, Y
• Y is a function of distance and two
angles.
• For 1 electron, Y corresponds to an
ORBITAL — the region of space within
which an electron is found.
• Y does NOT describe the exact
location of the electron.
• Y2 is proportional to the probability of
finding an e- at a given point.
Ulivina Pratini (127795086) 05/07/2014

26. Y2 is proportional to the probability
of finding an e- at a given point.
Ulivina Pratini (127795086) 05/07/2014

27. • An atomic orbital is defined by 3 quantum
numbers:
– n l ml
• Electrons are arranged in shells and
subshells of ORBITALS .
• n  shell
• l  subshell
• ml  designates an orbital within a subshell
Ulivina Pratini (127795086) 05/07/2014

28. Quantum Numbers
mmll (magnetic)(magnetic) --l..0..+ll..0..+l Orbital orientationOrbital orientation
in spacein space
ll (angular)(angular) 0, 1, 2, .. n0, 1, 2, .. n--11 Orbital shape orOrbital shape or
typetype ((subshellsubshell))
n (major) 1, 2, 3, .. Orbital size and
energy = -R(1/n2)
Total # of orbitals in lth subshell = 2 l + 1
SymbolSymbol ValuesValues DescriptionDescription
Ulivina Pratini (127795086) 05/07/2014

29. Shells and Subshells
For n = 1, l = 0 and ml = 0
There is only one subshell and that
subshell has a single orbital
(ml has a single value ---> 1 orbital)
This subshell is labeled s (“ess”) and
we call this orbital 1s
Each shell has 1 orbital labeled s.
It is SPHERICAL in shape.
Ulivina Pratini (127795086) 05/07/2014

30. s Orbitals
All s orbitals are spherical in shape.
Ulivina Pratini (127795086) 05/07/2014

31. When l = 1, there is
a PLANAR NODE
through the
nucleus.
planar node
Typical p orbitalp Orbitals
For n = 2, l = 0 and 1
There are 2 types of
orbitals — 2 subshells
For l = 0 ml = 0
this is a s subshell
For l = 1 ml = -1, 0, +1
this is a p subshell
with 3 orbitals
Ulivina Pratini (127795086) 05/07/2014

32. The three p
orbitals lie 90o
apart in space
pz
py
px
90 o
A p orbital
p orbitals (2)
Ulivina Pratini (127795086) 05/07/2014

33. p-orbitals(3)
px py pz
2
3
n=
l =
Ulivina Pratini (127795086) 05/07/2014

34. For l = 2, ml = -2, -1, 0, +1, +2
 d subshell with 5 orbitals
For l = 1, ml = -1, 0, +1
 p subshell with 3 orbitals
For l = 0, ml = 0
 s subshell with single orbital
For n = 3, what are the values of l?
l = 0, 1, 2
and so there are 3 subshells in the shell.
d Orbitals
Ulivina Pratini (127795086) 05/07/2014

35. d Orbitals
IN GENERAL
the number of NODES
= value of angular
quantum number (l)
s orbitals have no planar
node (l = 0) and
so are spherical.
p orbitals have l = 1, and
have 1 planar node,
and so are “dumbbell”
shaped.
d orbitals (with l = 2)
have 2 planar nodes
typical d orbital
planar node
planar node
Ulivina Pratini (127795086) 05/07/2014

36. Boundary surfaces for all orbitals of the
n = 1, n = 2 and n = 3 shells
2
1
3d
n=
3
There are
n2
orbitals in
the nth SHELL
Ulivina Pratini (127795086) 05/07/2014

37. 05/07/2014Ulivina Pratini (127795086)